Nuorium Optimizer V26 の新機能
1. ソルバ/ライブラリ
分枝限定法
発見的探索を強化しました。これにより、弊社のベンチマークセット(747 問)で 60 秒以内に実行可能解の求まる数が 85% から 91% に向上しています。
スパース単体法 hsimplex
スパース単体法 hsimplex に以下の前求解 (presolve) を実装しました。
- Empty row: 空の行を取り除きます。
- Singleton row: 単一の変数からなる制約式を取り除きます。
- Redundant and forcing constraints: 変数のバウンド情報を利用して制約式の除去や変数の固定を行います。
- Empty column: 空の列を取り除きます。
- Removing fixed variables: 固定変数を取り除きます。
- Bound propagation: 制約式を利用して各変数のバウンド情報を狭めます。
実務に現れる問題は往々にして除去可能な変数や制約式をもちます。そのような問題では hsimplex による求解速度の向上が見込めます。
WLS
- 目的関数と制約式が線形である最適化問題に対し、従来扱えるのは整数変数のみの問題まででしたが、連続変数を含む問題(混合整数計画問題)に対して解けるようになりました。Nuorium Optimizer V26 新機能を活用!重み付き局所探索法を用いた 2D Strip Packing Problem の求解
- 目的関数と制約式が線形である最適化問題に対し、単一の整数変数に対する近傍操作を flip(変数値を ±1 する操作)から jump(ペナルティ関数を最小化する点へ移動する操作)へ変更しました。単一の連続変数に対しても、同様の近傍操作が適用されます。
- PySIMPLE から変数の添字グループ情報を受け取る事により、「割当てを意味する変数」に対する近傍を拡大しました。一般化割当問題などの最適化問題に対し、割当構造を明示的に指定することにより、探索性能が向上されます。
2. PySIMPLE
詳細は PySIMPLE マニュアル 更新履歴 をご覧ください。
添字グループ情報
変数の添字グループ情報を指定できるようになりました。メタヒューリスティクスアルゴリズム wls へ、「割当てを意味する変数」の情報を明示的に渡せます。割当構造をもつ最適化問題に対し、探索性能の向上が見込めます。
変数の値固定
変数の値を現在値に固定するメソッド Variable.fix を追加しました。また、固定した値を解除するメソッド Variable.unfix も利用できます。
添字付き get メソッド
get メソッドを Parameter/Variable/Expression/Constraint に追加しました。
wls の連続変数対応
メタヒューリスティクスアルゴリズム wls で整数変数だけでなく連続変数を扱えるようになりました。連続変数を使う際は、目的関数と制約式が線形である必要があります。
3. V25 との互換性
- 解法 dual_simplex は廃止されました。
- C++SIMPLE 集合 Set への追加 add への操作に上限が設定されました。一つの集合に対する追加操作が多すぎるとエラーとなります。
- PySIMPLE の互換性については PySIMPLE マニュアル 更新履歴 をご参考ください。
Nuorium Optimizer V25 の新機能
1. ソルバ/ライブラリ
スパース単体法 hsimplex
双対単体法が (凸) 二次計画問題に適用できるようになりました。本手法は、最適解においてアクティブな制約が少ない問題に対して効率的に動作します。
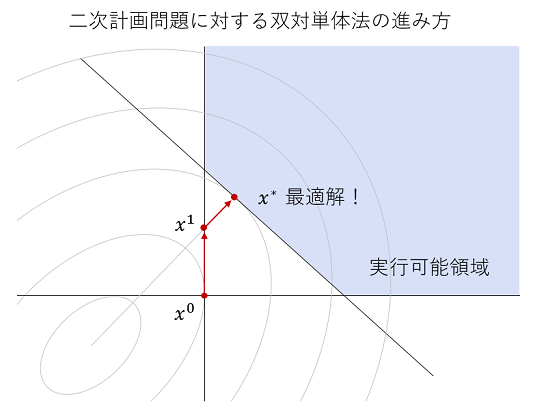
二次計画問題に対する双対単体法は、線形計画問題に対する同手法と同様に、最適性を保持しつつ実行可能性を求めるアルゴリズムです。 スパース単体法 hsimplex は PySIMPLE から利用できます。求解アルゴリズムの設定方法は下記リンクをご覧ください。
なお問題が線形計画問題であるか二次計画問題であるかの判定は自動的に行われるので、オプションで指定する必要はありません。
解の修復(repair)の求解オプション追加と性能改善
分枝限定法における解の修復(repair)において、積極的に修復をおこなう aggressive と、反復回数の上限を設定する repairIteration を追加しました。 また、弊社のベンチマークセットにおいて、600 秒以内に実行可能解を発見した問題数が V24 に比べて 30 % 改善しました。
求解オプションの設定方法は次の通りです。
- nuopt.prm における設定方法
begin
branch:repairSolution=aggressive
branch:repairIteration=20
end
- C++SIMPLE における設定方法
options.branchRepairSolution = "aggressive";
options.branchRepairIteration = 20;
- PySIMPLE における設定方法
problem.options.branchRepairSolution = Options.Branch.RepairSolution.AGGRESSIVE
problem.options.branchRepairIteration = 20
※ 補足:解の修復(repair)について 解の修復(repair)はユーザーが与えた解を修復して実行可能解を得る機能です。 解を修復するために 2 段階の求解を繰り返します。1 段階目の求解では実行不可能性(制約条件の違反量)を最小化します。これは元の数理最適化問題と同じぐらい難しいため、一部の整数変数を固定することで問題規模を縮小して求解します。2 段階目は実行不可能性に上限を与えて、その範囲内で元の数理最適化問題を求解します。この時も一部の整数変数を固定して問題規模を縮小します。このように、変数固定に加えて 2 段階の求解を繰り返すことで実行不可能性を最小化して解を修復します。
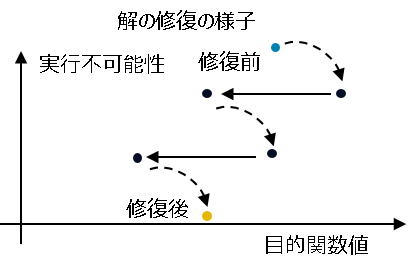
2. PySIMPLE
詳細は PySIMPLE ドキュメント更新履歴 をご覧ください。
分枝限定法の終了条件をコールバック関数で判定
分枝限定法の終了条件を Python のコールバック関数で与えられるようになりました。
wcsp の一般整数変数対応
制約充足問題に対するメタヒューリスティクスアルゴリズム wcsp で 0-1 整数変数 だけでなく整数変数を使えるようになりました。
3. マニュアル
ソルバの求解オプションについて、各モデリング言語( PySIMPLE, C++SIMPLE, RSIMPLE)での設定方法が「 Nuorium Optimizer マニュアル」に統一的に記述されるようになりました。
4. V24 との互換性
- 従来の C++ ベースのモデリング言語「SIMPLE」は、「C++SIMPLE」という名前でマニュアル等に記載されるようになりました。
- PySIMPLE の互換性については PySIMPLE マニュアル 6. 更新履歴 をご参考ください。
Nuorium Optimizer V24 の新機能
Nuorium Optimizer V24 の新機能情報を公開中です。
1. ソルバ/ライブラリ
スパース単体法 hsimplex
スパース LP 単体法 (primal/dual)
線形計画問題に対する解法の一つに単体法と呼ばれるアルゴリズムがあります。 V23 にて、弊社従来の単体法よりもスパース性をより活用する単体法 (hsimplex) を導入しました。 V24 ではこのコードをさらに改良し、主単体法及び双対単体法を整備しました。 制約式に現れる変数が極めて少ない問題(ハイパースパース性を持つと呼ばれます) に対して高速に動作しますので、ぜひお試しください。
QP 単体法 (primal)
V24 にて、凸二次計画問題に対する解法の一つである QP 単体法を導入しました。 LP 単体法と同様にハイパースパース性をもつ問題に対して高速に動作します。 凸二次計画問題を解く際には、解法の一つとしてぜひご検討ください。
2. PySIMPLE
詳細は PySIMPLE ドキュメント更新履歴 をご覧ください。
IIS オブジェクトの取得
線形計画問題において互いに矛盾する制約式がある場合、その最小の組を IIS(Irreducible Infeasible Set) と呼びます。 この IIS を Python オブジェクトとして取得できるようになりました。 実行不可能な場合に、原因となる制約の特定や、その制約に対するケアなどを自動化する強力な手助けとなります。
PySIMPLE オブジェクトのシリアライズ
Python には、Python オブジェクトをシリアライズ(直列化)して扱うことのできる pickle という機能が標準で用意されています。 PySIMPLE オブジェクトを pickle と同様にシリアライズ(直列化)する機能が追加されました。
3. RSIMPLE
統計解析ソフトウェア R をインターフェイスとする「RNUOPT」が、「RSIMPLE 」として Nuorium Optimizer に加わります! RSIMPLE を通じて、R が備えている統計解析機能と Nuorium Optimizer の提供する数理最適化機能を連携した分析が可能となります。
4. Nuorium
ターミナル機能
Nuorium ではこれまでモデリング言語 SIMPLE の記述を中心に、より快適・円滑にモデル編集や解析ができるように、テキストエディタとしての側面も重要視して強化してきました。
この汎用的な高機能テキストエディタとしての特徴はそのままに、Nuorium の version 6 では更にターミナル機能を搭載しました。 cmd (コマンドプロンプト) や PowerShell (パワーシェル) といったシェルを呼び出す端末として、Nuorium を利用することができます。
例えば編集中のモデル model.smp を表示したまま、画面分割を行ってコマンドプロンプトを呼び出し、mknuopt model.smp というビルドコマンドを実行することもできます。
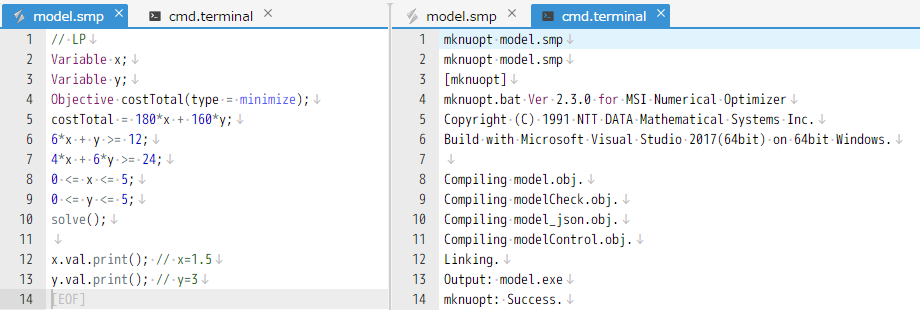
ビルドに成功すれば、そのまま model.exe と入力してモデルも実行できます。 Ctrl-Shift-T でコマンドプロンプトを外部呼び出しできますが、version 6 より Nuorium 上でも呼び出せるようになります。
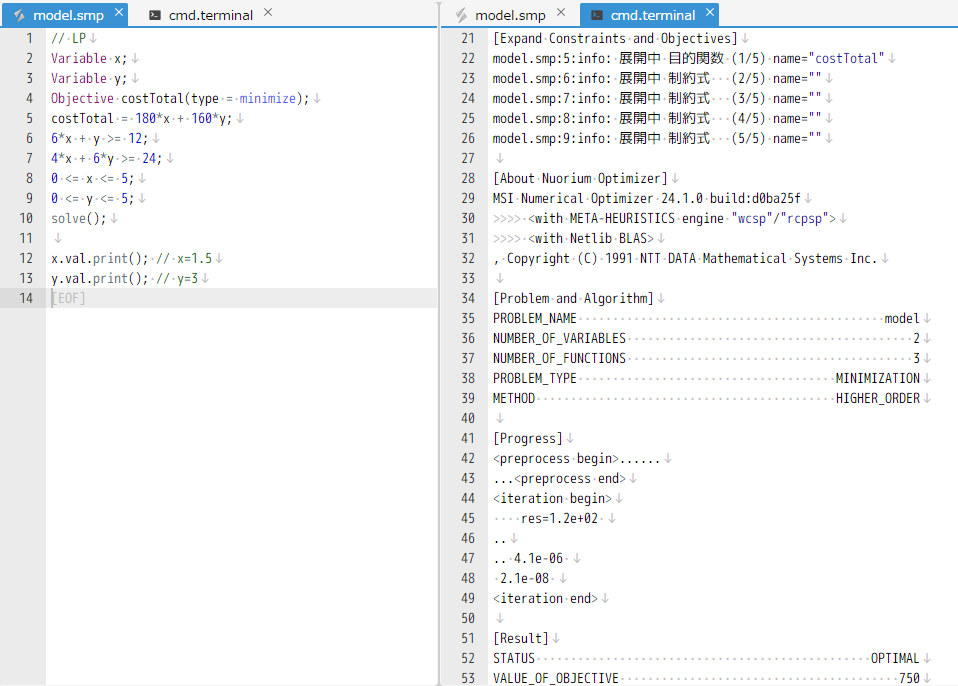
ターミナル機能はシェル設定画面からユーザ設定が可能です。 下図は Python のインタラクティブモードの呼び出し設定です。
これによって例えば PySIMPLE をインタラクティブに使用することも可能になりました。 ターミナル機能の搭載で Nuorium 上での編集作業がより効率的に、そして多面的になりました。
一括変換機能
以下の頻出する文字種別間の変換に関して、一括変換機能を追加しました。
句読点の「。」「、」「.」「,」間の変換 英数字の半角全角変換 括弧類の半角全角変換 日々の文書作成の他、技術文書の作成や各種データの整形などにお役立てください。
5. 定式化技法集

開発版をご購入されたユーザー様がモデリングを独自に行う際に、役立つ様々なテクニカルドキュメントを公開します。
私たちは『特殊なケースでの定式化技法』という資料を公開しておりましたが、この機会に大幅に見直し、実践的な実務家となるために必要な定式化の様々な技法の整理・充実を図りました。
重要となる概念ごとに一つのトピックとしてまとめ、それらの関連性についても整理しております。
実際に役立つテクニックばかりで、実務家としてモデリングに取り組む際には必携です!
定式化技法集 のページよりご覧ください。
6. V23 との互換性
PySIMPLE の互換性については PySIMPLE マニュアル 6. 更新履歴 をご参考ください。
Numerical Optimizer V23 の更新情報
Numerical Optimizer V23 の新機能等を紹介いたします。
1. ソルバ/ライブラリ
新アルゴリズム WLS
Numerical Optimizer に新たなメタヒューリスティクス解法 wls(重み調整局所探索法)が追加されました。 整数計画問題に対して、データ構造「隣接リスト」を用い効率的に解を探索します。 二次の目的関数やソフト制約付きの最適化問題も取扱可能です。 集合被覆問題、集合分割問題などをはじめとしたすべての係数が 0 か 1 の制約式を多く含む問題に対してより高速な求解が実現されます。 以下の例のように、PySIMPLE で従来通り定式化を記述した後アルゴリズムに wls を指定するだけで使用可能です。
## PySIMPLE 新アルゴリズム wls のサンプル
from pysimple import *
x = BinaryVariable()
y = IntegerVariable(lb=-1, ub=3)
z = BinaryVariable()
p = Problem(name="wlsサンプル")
p += x - 2 * y + 3 * z
p += x + z == 2
p += 3 * x + 2 * y - z <= 0
p.options.method = "wls" # アルゴリズムに wls を指定
p.solve() # wls で求解される
解の修復機能
Numerical Optimizer の分枝限定法に解の修復機能が追加されました。 この機能により、制約を満たしそうな整数変数の値を与えて、連続変数の値をソルバに決定させる、などが可能となります。 以下の例では 0-1 整数変数 x, y の値だけ与えておき、連続変数 z の値をソルバに決定させています。 解の修復が終わると通常の分枝限定法を開始します。
// SIMPLE 解の修復機能のサンプル
IntegerVariable x(type=binary); IntegerVariable y(type=binary);
Variable z; z >= 0;
x + y >= 4 - z;
Objective f(type=minimize); f = z;
options.branchRepairSolution = "on"; // 解の修復機能を有効にする
x = 1; y = 1; // 整数変数 x, y の値のみ与える
solve(f); // 連続変数 z の値を修復してから分枝限定法を開始
## PySIMPLE 解の修復機能のサンプル
from pysimple import *
x = BinaryVariable(init=1) # 整数変数 x を定義して初期値を与える
y = BinaryVariable(init=1) # 整数変数 y を定義して初期値を与える
z = Variable(lb=0)
p = Problem()
p += x + y >= 4 - z
p += z
p.options.branchRepairSolution = True # 解の修復機能を有効にする
p.solve() # 連続変数 z の値を修復してから分枝限定法を開始
2. PySIMPLE
詳細は PySIMPLE ドキュメント更新履歴 をご覧ください。
凸二次計画問題への対応
制約式、目的関数に二次式を含む凸二次計画問題を扱うことができるようになりました。
メタヒューリスティクスアルゴリズム wcsp/wls の利用
重み付き制約充足問題に対するメタヒューリスティクス解法 wcsp を呼び出せるようになりました。 また、新たなメタヒューリスティクス解法 wls を利用できるようになりました。
高速化
V22.1.0 と比較して 19.5% の高速化を達成しました。
3. Nuorium
ライブリロード機能
ドキュメント化した SIMPLE ファイルや Markdown ファイルを、ブラウザを通して HTML ドキュメントとして同期表示するライブリロード機能を追加しました。
レポート作成を追加
最適化計算を総合的に要約するレポートを作成する機能を追加しました。簡易的な報告であれば、この機能によって即座にレポートを作成できます。
ステータスバーに実行時の進捗報告
最適化計算中の進捗状態をステータスバーに表示できるようになりました。 これによって現在稼働中のマルチスレッド数や、終了条件の進捗をリアルタイムに監視できるようになりました。
実行関連
実行単位が無指定の場合は、拡張子に応じた実行(ユーザ設定可能)を行う挙動に変更しました。 これにより SIMPLE ファイル以外の場合について、ユーザはデフォルトでよく使う実行形式を選択可能となります。 例えば .py の拡張子に対して、好みの python.exe を指定するといったご利用方法となります。
キーバインド追加
マルチカーソルから連番を生成できるようになりました。これにより、より省力な編集作業が可能になります。
Grep バッファ
エディタ上で横断的に正規表現検索が可能な Grep バッファを搭載しました。Nuorium で完結した作業をこれまで以上に体験することが可能となりました。
4. V22 との互換性
options.maxmemや分枝限定法の出力における mem の単位を MB から MiB に統一しました。- SIMPLE において wcsp のペナルティ取得関数名を変更しました。
result.getHardPenaltyBest()をresult.hardPenaltyに変更しました。result.getSemihardPenaltyBest()をresult.semiHardPenaltyに変更しました。result.getSoftPenaltyBest()をresult.softPenaltyに変更しました。
- method を指定せずに MINLP を解こうとした場合、エラーとなるように変更しました。
- PySIMPLE の互換性については PySIMPLE マニュアル 6. 更新履歴 をご参考ください。
Numerical Optimizer V22 の更新情報
Numerical Optimizer V22 の新機能等を紹介いたします。
1. 計算ライブラリ
並列計算機能と分枝限定法の強化をおこないました。
並列計算機能の刷新
分枝限定法やメタヒューリスティクス解法 wcsp の並列計算機能を刷新しました。 これにより Linux や Mac 環境、さらにはランタイム環境をお持ちの方にもご利用いただけるようになりました。 利用方法は非常に簡単です。分枝限定法の場合はモデルファイルでスレッド数を指定します。
options.bbthreads = 4; // 4 スレッドで実行する
// 並列分枝限定法の手法を変更する場合は以下の記述を追加します
// options.branchParallelMethod = "racing"; // デフォルト
// options.branchParallelMethod = "subtree";
// options.branchParallelMethod = "deterministicRacing";
wcsp の場合はモデルファイルでスレッド数と試行回数を指定します。
options.wcspthreads = 4; // 4 スレッドで実行する
options.wcspTryCount = 12; // 試行回数を設定する
// 各スレッドで 12 / 4 = 3 回 wcsp が実行されます
ビルド時に特別なオプションは必要ありません。 ビルドしたバイナリをランタイム環境に配置して並列計算をおこなうこともできます。
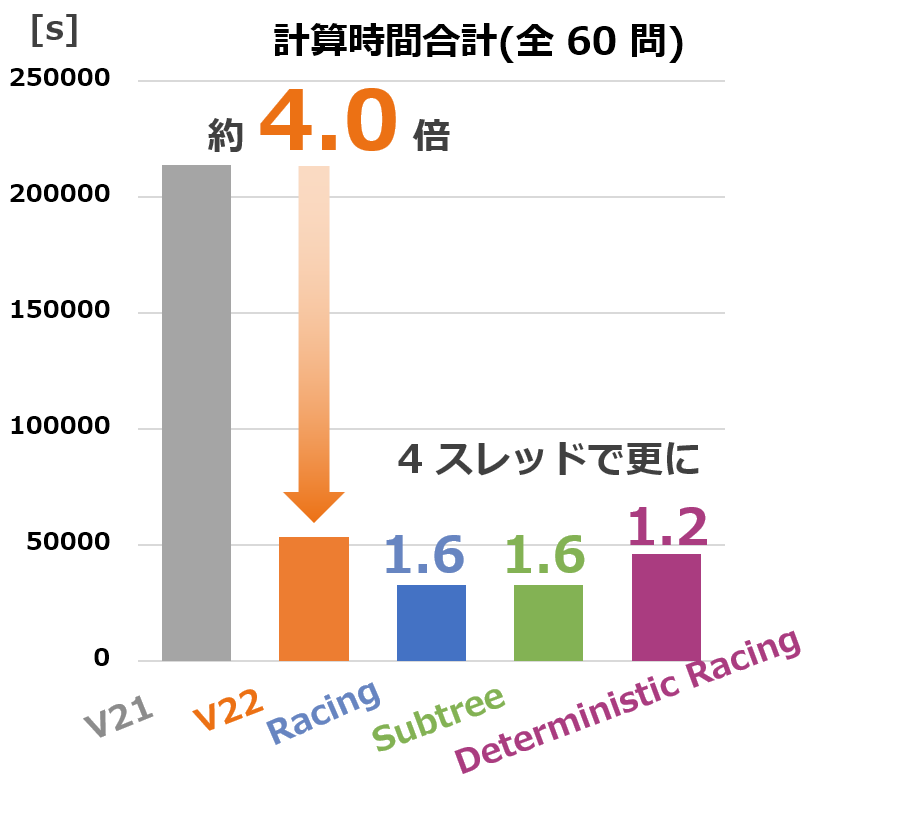
分枝限定法の強化
分枝限定法の前処理や切除平面法の強化をおこないました。 特に、切除平面法の強化により発電機の起動停止運転計画問題において大幅な高速化をおこないました。
2. PySIMPLE
詳細は PySIMPLE ドキュメント更新履歴 をご覧ください。
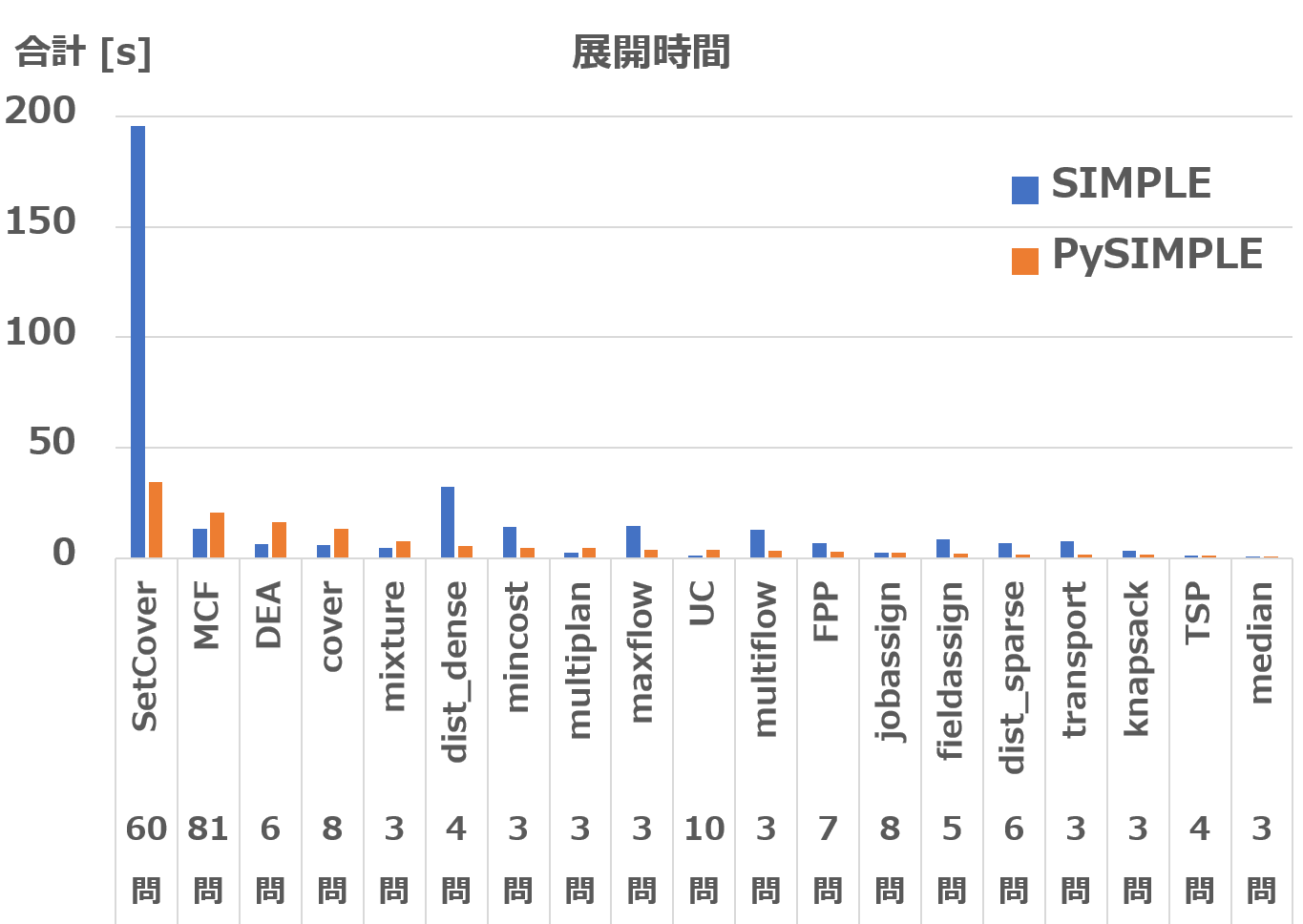
式展開が劇的に高速化
PySIMPLE 1.1.0 では式展開が劇的に高速化されました。 1.0.1 と比較して 10 倍以上の高速化を達成し、SIMPLE と比較しても遜色のない速度になりました。
対応環境の強化
動作環境として Linux,Mac がサポートされるようになり、最新の Python 3.8 にも対応しました。
3. Nuorium
実行環境およびモデリング環境の拡充を行いました。
モデル・データ連係機能を改修
モデル・データ連係画面を廃止し、JSON 形式でファイルパスを指定する方式に変更しました。 外部コマンドの呼び出しが可能になったことで、例えば PySIMPLE の呼び出しなど、より包括的な実行環境が利用可能となりました。
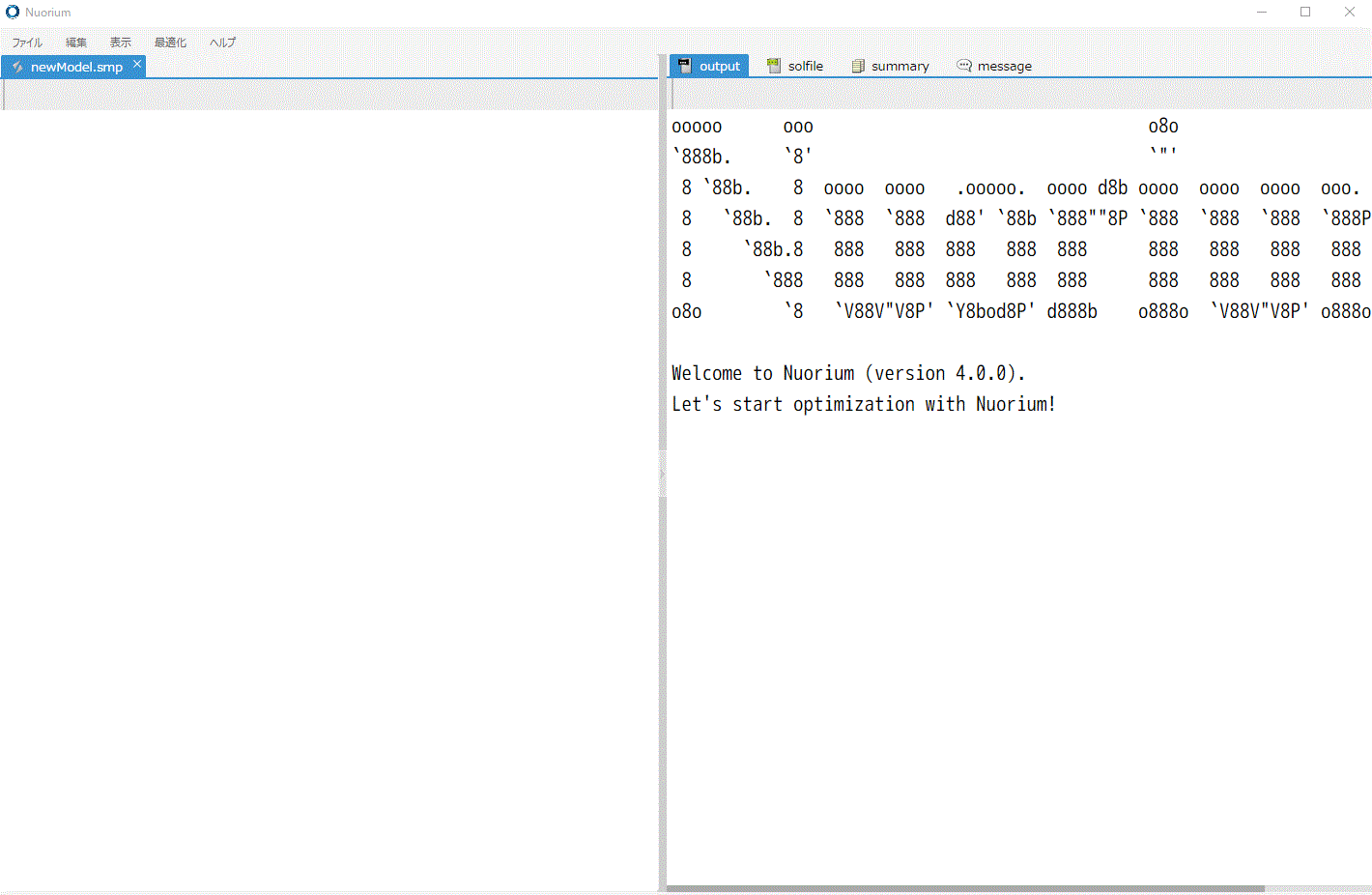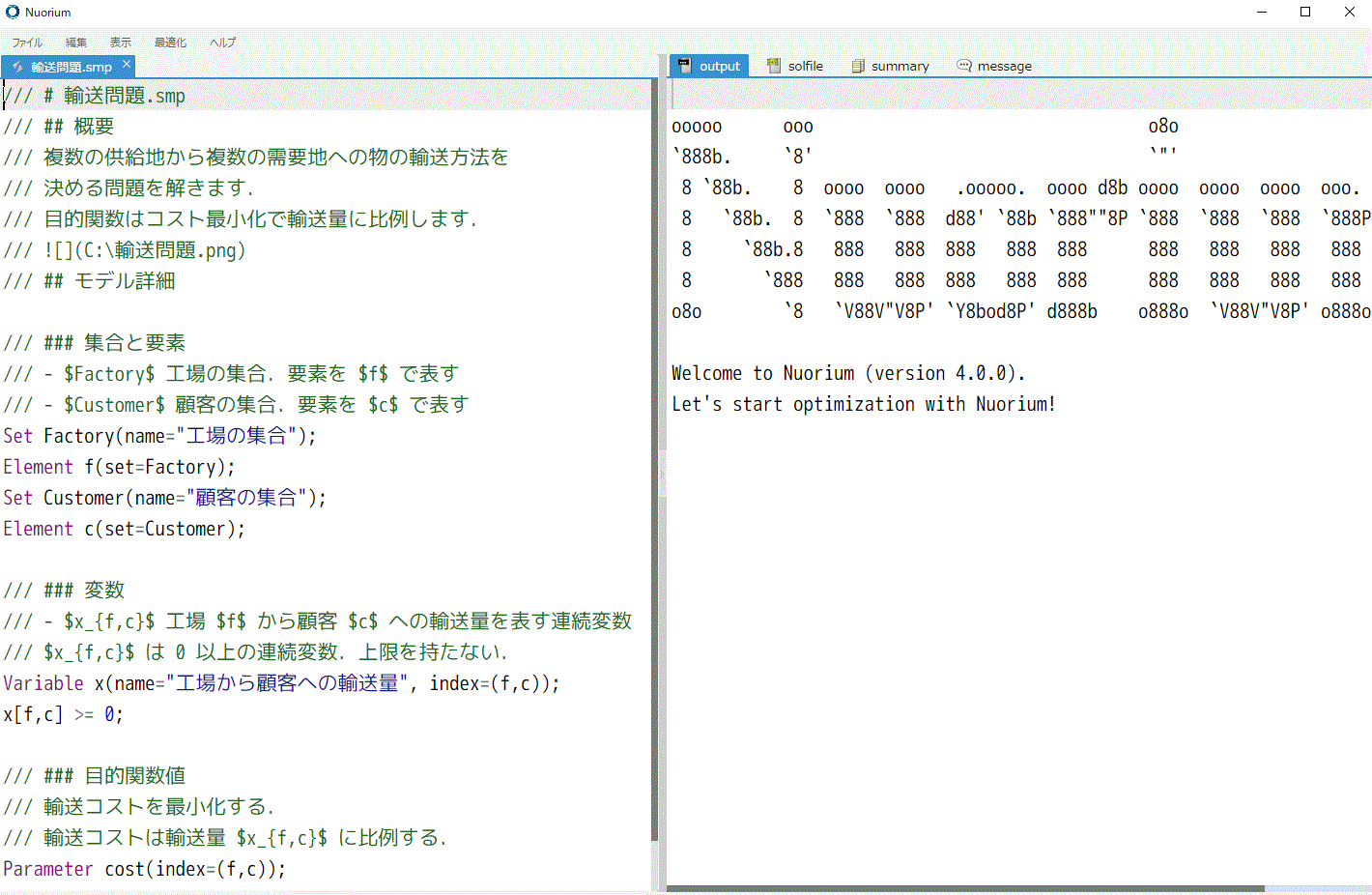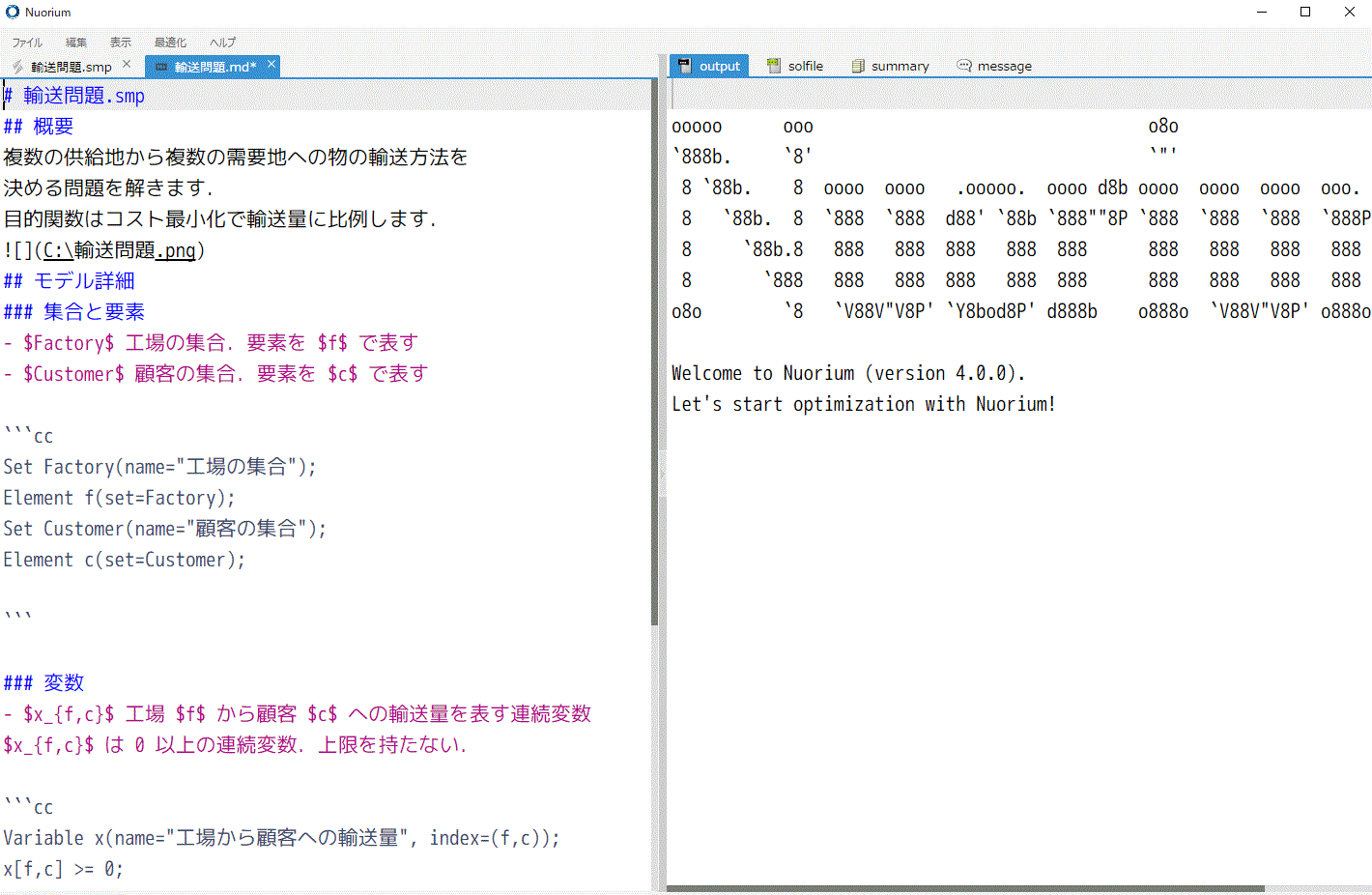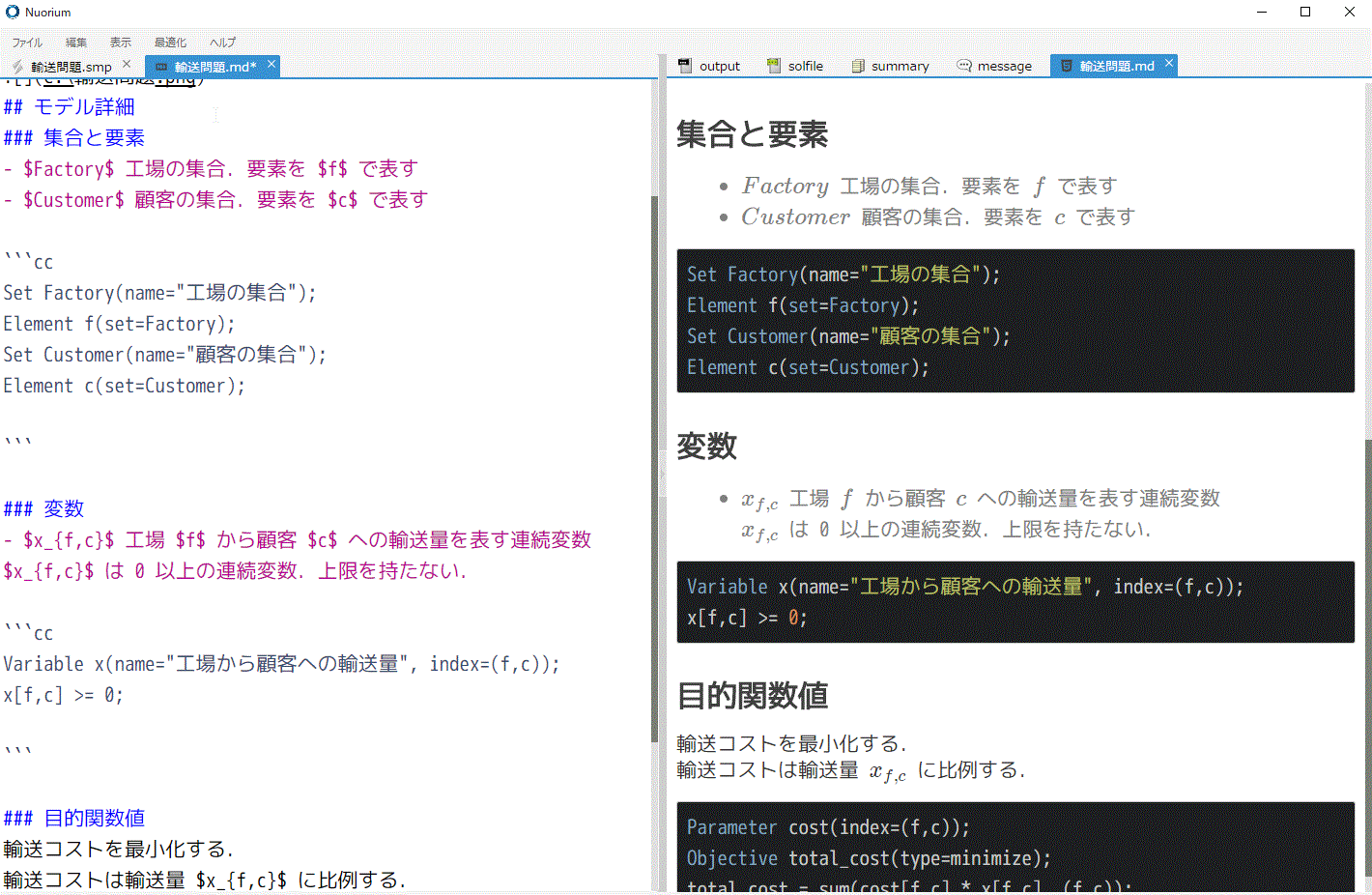
SIMPLE と Markdown の連携機能
SIMPLE ソースコードに Markdown を記述できる特別なコメントシンタックスを追加しました。 これによりモデルの保守性の向上に役立てられるようになりました。
4. V21 との互換性
- 相対 gap の定義が変更になりました。定義の変更により
options.relgaptolを用いて停止条件を指定する場合、停止されるタイミングが V21 と V22 で異なる可能性があります - ビルド時の並列化オプション(-parallel)が廃止になりました。並列計算機能をご利用になる場合はオプションをつけずにそのままビルドしてください
hardConstraint(),semiHardConstraint(),softConstraint()によって既に設定した制約式の重みを変更した場合、警告 SIMPLE 560 が出力されます- 代入の左辺の添字が一意ではない場合、SIMPLE 72 が発生します
OrderedSet I = "1 2 3 4"; Element i(set = I); Set V = "0 1"; Element v(set=V); Parameter tmp(index=v); tmp[i % 2] = 1; // i = 1, 2, 3, 4 に応じて i % 2 = 1, 0, 1, 0 となります。 // i % 2 の値が重複しているため SIMPLE 72 を返します。 - ビルドコマンド mknuopt は V16 以前の ufun 形式に対応しません
- Nuorium のデータ連係に用いる .nuo ファイルを廃止しました。JSON 形式によるデータ連係機能をご利用ください
Numerical Optimizer V21 の更新情報
Numerical Optimizer V21 の新機能等を紹介いたします。
Python インタフェース PySIMPLE
ご要望を多くいただいておりました Python インタフェースを実現しました!
SIMPLE の利便性をそのまま移植
下記は PySIMPLE を用いたモデリングの例です。 モデリング言語 SIMPLE との互換性を満たしつつ、Python で自然とモデリングができる設計になっております。
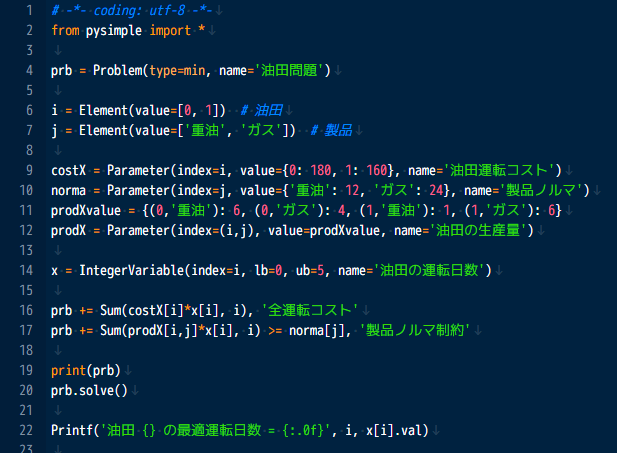
インタプリタ利用可能
もちろんインタプリタとしてもご利用いただけます。 Jupyter Notebook 上でも動作します。
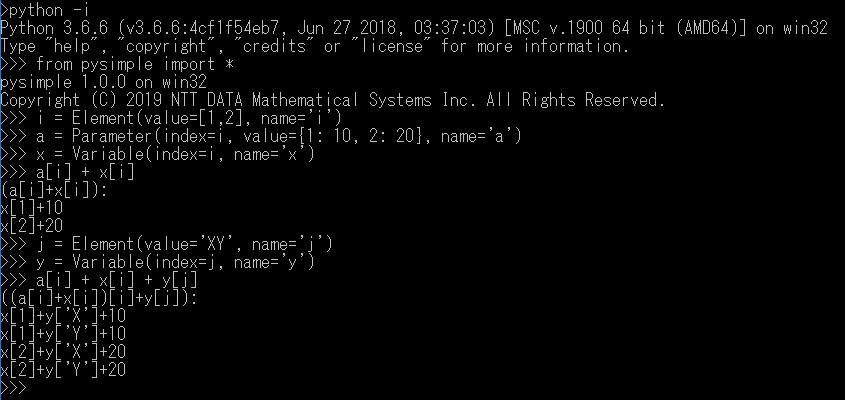
name 属性自動付与
name 属性を明示的に付与しなかった場合でも自動で付与されます。 これは宣言時だけでなく、式や制約式などの計算結果に対しても適用されます。 上記の油田問題で name 属性を付与しなかった場合、問題を表示すると次のような出力を得ます。
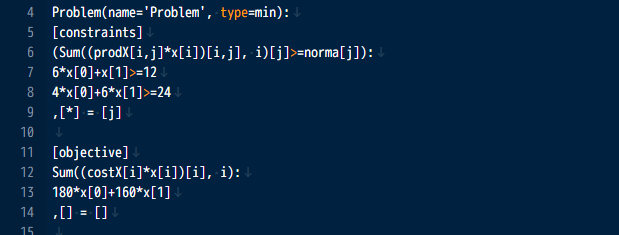
Python モジュールとして利用可能
PySIMPLE は Python のモジュールとして実装されています。 ユーザ様がご利用の Python 環境にインストールして頂くことにより、これまでにお使いの Python 環境でそのままご利用いただけます。
また、Python のモジュールのため、前処理、後処理などのデータ加工ともスムーズに連係が可能です。 データ連係を意識した設計となっており、Python におけるデータ構造を直接渡したり、計算結果をお手軽に Python オブジェクトに dump できるようになっています。
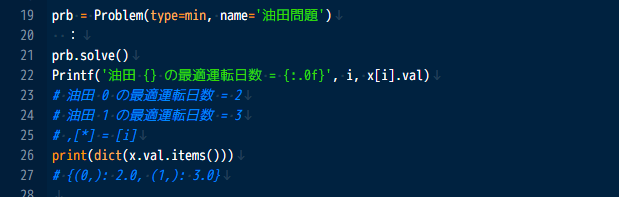
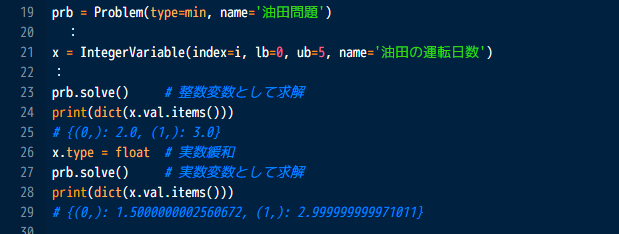
変数の実数緩和
変数の属性を宣言後に変えることができるようになります。 この機能により、整数変数で解が見つからない場合に、実数緩和して再求解を行う操作が簡単に実現できます。
よりコンパクトなスパースモデリング
疎集合 IJ に対して、SIMPLE では、
![]()
または、
![]()
と記述していた場合、PySIMPLE では、
![]()
と記述するよう、より簡潔に一本化されます。 (次元のインデックスは SIMPLE は 1 始まり、PySIMPLE では 0 始まりになります。)
この記法は PySIMPLE において、条件付きの式を記述する際にも利用できますので是非お試しください。
他にも 0-1 整数変数を表す新キーワード BinaryVariable など細かな機能追加もございます。
Numerical Optimizer V20 の更新情報
Numerical Optimizer V20 の新機能等を紹介いたします。
1. Nuorium V3
version 3.0.0 ではスタンドアローン版の大幅な機能強化と拡張を行いました。 Nuorium でこれまでになかったモデル記述を体験できます。 そしてモデル記述以外にもファイル編集を本格的に行うことができます。 モデリング補助機能を拡充し、プロユースのテキストエディタとして利用可能なように機能強化したことが改良点の大きな特徴です。 実に多くの機能強化と拡張を図っており、そのすべてをここではご紹介しきれませんが、以下に主要な幾つかをご紹介します。
モデリング補助機能の拡充
インスタンスハイライト
SIMPLE の記述が数百から数千行単位になってきますと、インスタンス名だけから、それが変数なのか定数なのか、はたまた集合や添字なのかといったことが一目では判別が難しくなってきます。 これまでは SIMPLE ファイルをビルドすれば、それらを一望することができました。 しかしそのような視点だけでなく、カーソル位置にあるインスタンスが何であるかも即時に知りたいものです。 version 3.0.0 ではそれが可能となりました。SIMPLE ファイルの編集と同時に今画面に見ているインスタンスが、変数なのか定数なのかといったことが一目できるようになりました。
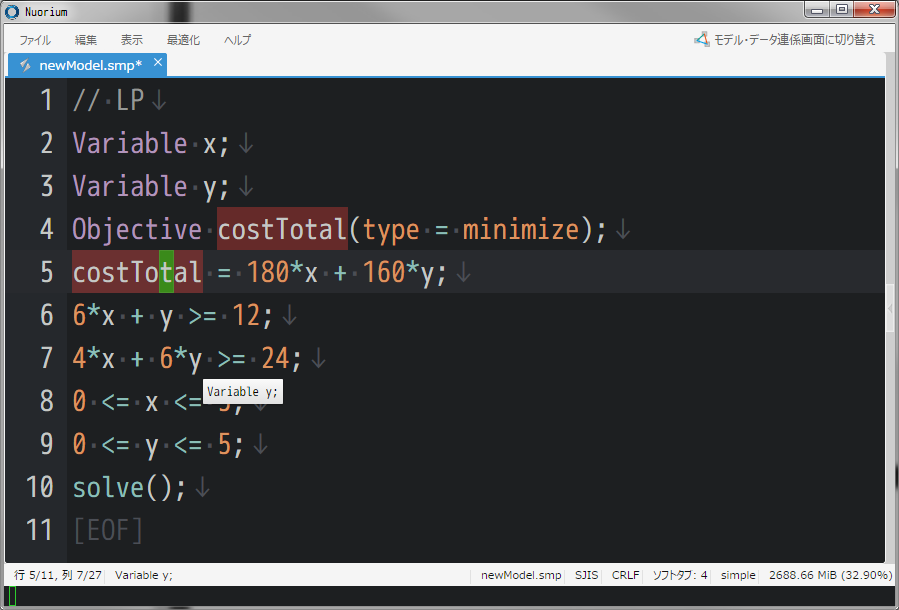
インスタンス選択
SIMPLE ファイルを編集中に、変数 foo を bar に変えたいという時があるかと思います。そのようなときにはインスタンス名だけを選択する必要があります。 文字列 "foo" やコメント // foo といった箇所を除いてインスタンス名 foo だけを変えたい場合です。 このようなことも version 3.0.0 では可能となりました。
インスタンスの記述行
ある変数 x が SIMPLE ファイルのどの行に記述されているかを、ビルド前に即時に表示する機能を追加しました。 また何行目にあるという表示とともに、その表示をクリックすることで、その行にジャンプできるタグジャンプ機能も同時に追加しております。 本機能によって、たとえ初めてモデル記述を見た場合でも、どの行にどのような形で記述されているかを、問題となっているオブジェクトだけに集中して情報を取得できます。
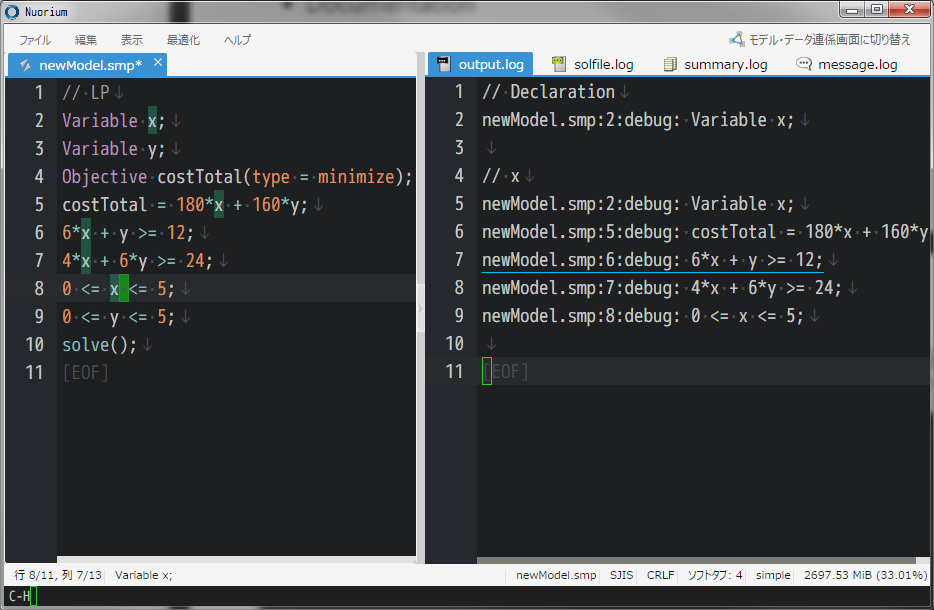
クラスごと記述行
SIMPLE ファイル全体で変数や定数、集合・制約式などいったものが、どこにどれだけ使われているかを、ビルド前に即時に表示する機能を追加しました。 これもタグジャンプ機能を同時に追加しております。 本機能によって、現在のモデル記述がどれだけの変数や定数を含んでいるのかといったことが、すぐに知ることができます。
エディタ機能の強化
対応言語の拡充
これまで SIMPLE ファイルとそのデータファイル (dat, csv) およびパラメータファイル (nuopt.prm) そして lp, mps ファイルのみが、Nuorium で編集できる対象でした。 この制限を取り払い、任意のテキストファイル形式を編集可能にしました。 そして C/C++, Python, R, JavaScript, TeX/LaTeX, Markdown など、言語ごとに適切なシンタックスハイライトを自動で行うようにしました。 対応する言語は約 120 言語で、なおかつインストール時点からこれらシンタックスハイライトを利用できます。
Emacs キーバインド
歴史あるテキストエディタの一つに Emacs がありますが、この操作感を体感できるキーバインドモードを組み込みました。 特に難しい設定をする必要がなく、クリック一つでいつでも Emacs のキーバインドを体感できるモードに切り替えることができます。 単純なキーバインドの変更だけではなく、インクリメンタルサーチやミニバッファ、キルリングも備え、単に C-f, C-b だけのような置き換えではなく、本格的なものとなっています。 普段、Emacs を利用されているユーザでも違和感なくご利用いただけるものと思います。 また C-h を Backspace にするなどといった自分好みにキーバインドを変更することも可能です。
略語展開
TeX/LaTeX のようなマークアップ言語は定型的な記述が繰り返されるため、それが面倒なところですが、予め略語を登録することで、この作業量を激減させることができます。 例えば略語 \eq とだけ打てば、equation 環境の雛形に展開するといった機能です。 略語は言語ごとにユーザが任意に複数設定することができ、多様で高速な編集が可能です。
TeX 数式プレビュー
数理最適化のようないわゆる数学が必要な業務・研究を遂行する上で、数式を含んだ文書を作成することが多々あるかと思います。 数式を記述する上で最も伝統的な言語でありデファクト・スタンダードは TeX/LaTeX でしょう。 昨今は TeXLive の登場によって、環境導入の敷居はほぼ全くないほどになり、後は書き方を覚えるだけで誰もが高品質の文書を作成できる時代になりました。 その中で数式が正しく打てているかが、コンパイル前に数式として視覚的にわかるととてもありがたいものです。 例えば \sum_{i\in I}x_i と記述して、いわゆるシグマ記号に下付き添字 i を伴った x というような数式が書けているかが、コンパイル前に知りたいものです。 Nuorium 上で TeX/LaTeX を編集すれば、記述と同時に数式をプレビューすることができます。 これは記述誤りによるコンパイル回数やデバッグ回数を大幅に削減します。 結果として思考を途切らせる事なく、編集作業に集中できることが期待できます。

Markdown プレビュー
TeX/LaTeX のような本格的な文書作成の他に、もっと気軽に文書を作成できる言語の代表格に Markdown があります。 Nuorium ではこれの編集とシンタックスハイライトはもちろんのこと、プレビュー機能も組み込みました。 Markdown の編集と同時にリアルタイムで、そのプレビューを見ることができます。
なお Markdown プレビューでは数式もプレビューできます。 Markdown における数式シンタックスは細かいものまで含めると少なくとも 20 種類以上ありますが、そのうち代表的と思われるもの、そして Pandoc との互換性があるものといった尺度で、プレビュー可能なシンタックスを選択いたしました。 多くの場合に数式プレビューがご利用できるようになっております。
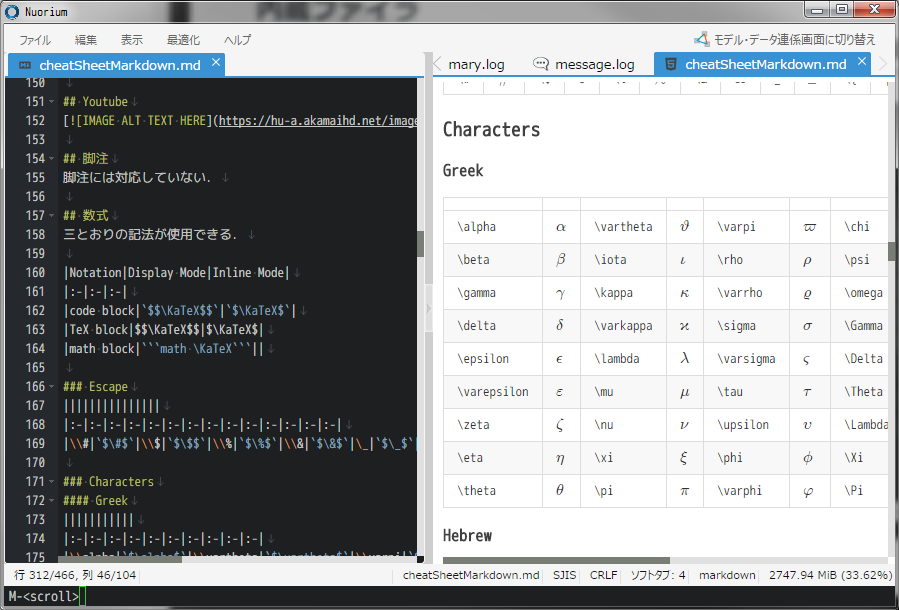
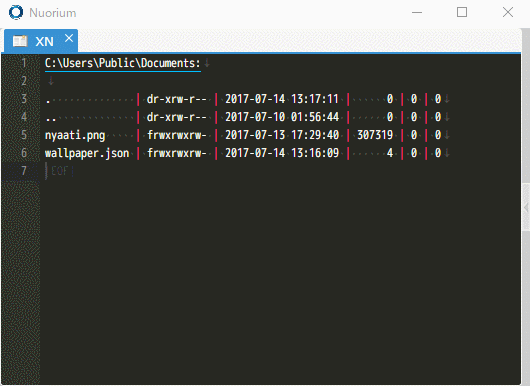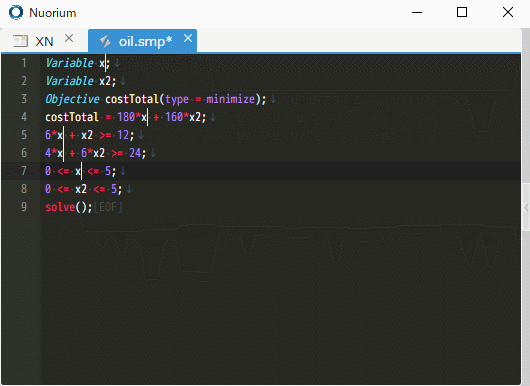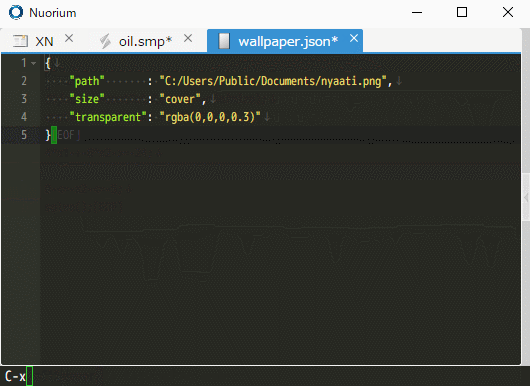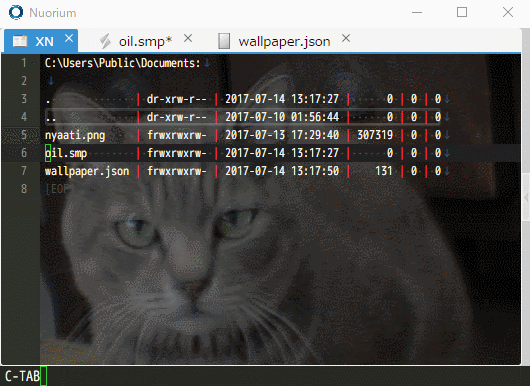
ファイラ
テキストファイルの編集の他に、ファイラ機能がご利用いただけます。 Nuorium 上からファイル自体のコピー・移動・削除やディレクトリの作成といった基本的な作業ができます。 ファイラはマークや削除フラグといった Emacs の dired とよく似た操作感も再現しています。 ファイラ機能により Nuorium を中断することなく、ディレクトリ・ファイル構成を編集いただけます。
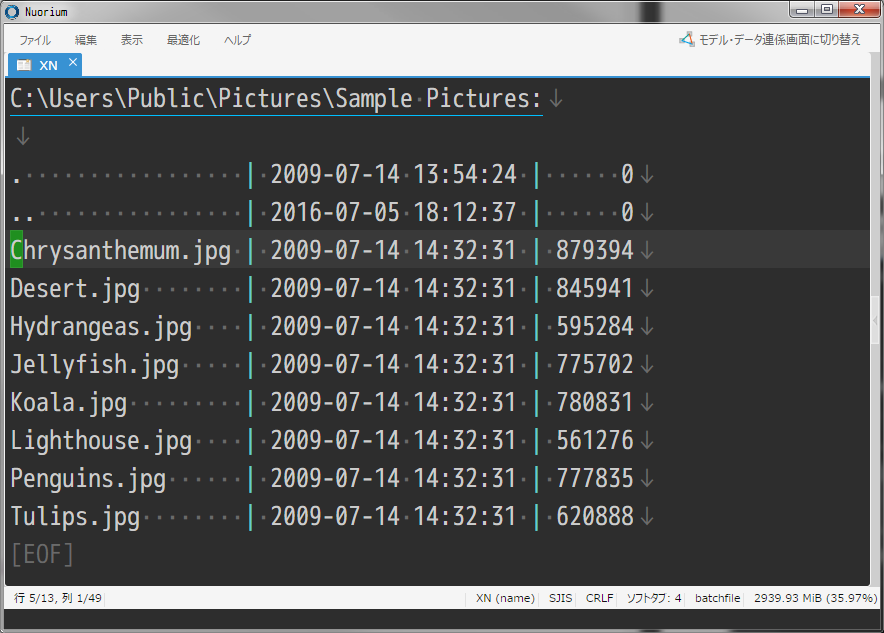
リファレンスマニュアル
Nuorium は version 3.0.0 に至って、実に様々な機能がご利用できるようになりました。 そこですべての機能について詳細に記述した公式のリファレンスマニュアルを作成しました。 上記で説明しきれなかった新機能についても書かれてあります。 お手元にリファレンスマニュアルを置いていただき、お困りの際にぜひともご一読いただければと存じます。
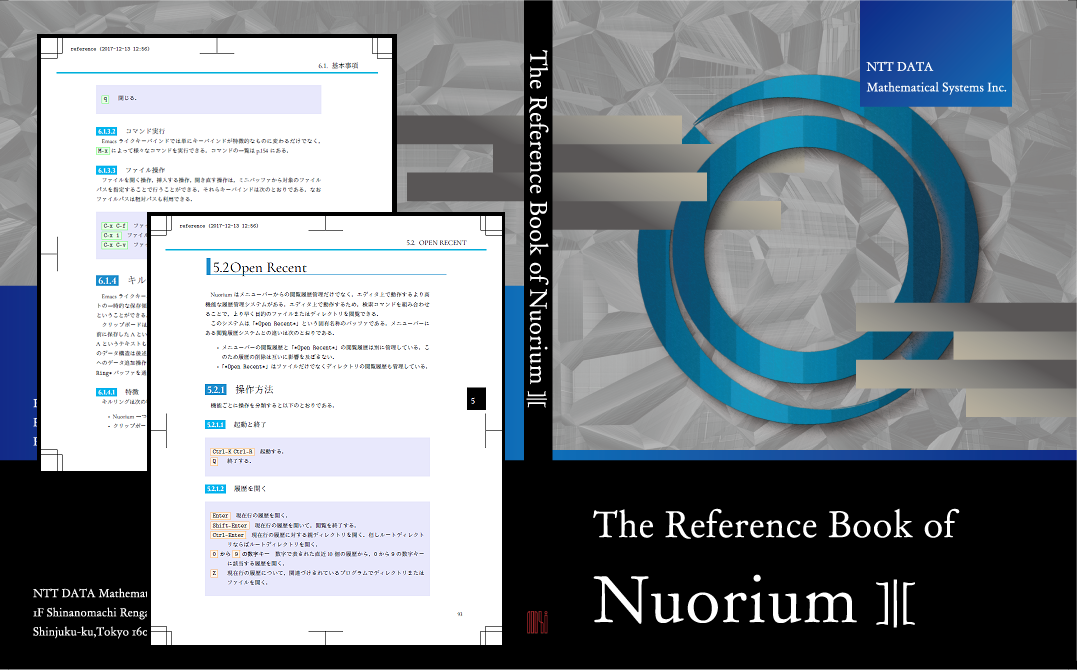
2. Excel 上で手軽に最適化
Excel アドインに最適化モデルのテンプレートが追加され、モデルを記述することなく手軽に最適化ができるようになりました。
テンプレートモデルは制約の追加、目的関数の変更など Nuorium を用いて自由にカスタマイズ可能なので実用的なモデルも手早く記述できます。
3. 強化された分枝限定法
搭載されている最適化アルゴリズムは更に磨かれました。
分枝限定法では新たなヒューリスティクスにより実行可能解が発見しやすくなり、切除平面法の改良によって最適性の証明までの時間が短縮しました。
より高速に、頑健になった最適化アルゴリズムをぜひお試しください。
Numerical Optimizer V19 の更新情報
Numerical Optimizer V19 の新機能等を紹介いたします。
1. Nuorium をブラッシュアップ
Nuorium は、数理最適化のモデリングや計算を強力に支援する Numerical Optimizer のための GUI 環境です。実際の業務で培われたエッセンスを凝縮し、よりプロフェッショナルに磨き上げました。
新たにスタンドアローンでも使えるようになった Nuorium で、軽快なモデリングをお楽しみください。

2. 生まれ変わった Excel アドイン
使いやすさを徹底追求しました。お使いの Excel 上でデータの登録、最適化の実行、結果の表示が、直感的な操作で実現できるようになり、手間が大幅に軽減されます。
3. 性能アップした分枝限定法
発電事業における分散電源の設備計画問題など実務であらわれる様々な問題を解くアルゴリズムである分枝限定法。このメモリ消費量を 1/3 にまで減らすことに成功しました。また高度な前処理技術により、速度も平均 10% アップしています。Numerical Optimizer の分枝限定法は「より速く」「より頑健」なアルゴリズムに進化し続けています。
Numerical Optimizer V18 の更新情報
Numerical Optimizer V18 の新機能等を紹介いたします。
1. Visual Studio 2015、Windows 10 対応
Microsoft Visual Studio 2015 および Windows 10 に対応しました。
2. GUI の刷新
キーワード補完機能等、モデル作成支援機能を強化し、今まで以上にモデルが作りやすくなりました。ワンクリック実行・モデルサマリ表示機能などにより、GUI 自体もより使いやすくなっています。エディタとして Ace を用いてモダンなデザインに仕上げていますので是非お試しください。
3. 線形計画問題のパフォーマンス向上
SIMD 命令を明示的に利用することにより Intel CPU において高次オーダー法の性能が改善されます。またデータ構造の見直し、64bit 整数型への対応により高次オーダー法(Matrix Free 含む)が一億変数を超える超大規模線形計画問題に対応可能となりました。線形計画問題に対して双対単体法が利用可能になりました。数十万変数の大規模問題において効果を発揮します。
4. 混合整数線形計画問題(MILP)のパフォーマンス向上
MILP ヒューリスティクスの強化により実行可能解が見つかりやすくなっています。分枝限定法フレームワーク全体の見直しにより、全体として求解時間が改善されています。
5. 離散最適化ヒューリスティクス WCSP 解の品質向上
モデル化そのものに起因してハード制約の違反が残ってしまう場合にも、ソフト制約違反がより改善される結果が出力されるように措置を施しました。
6. マニュアル刷新
一部マニュアルに関してオンラインマニュアルを公開します。その他のマニュアルに関しても pdf の検索機能強化等行いました。
Numerical Optimizer V17 の更新情報
Numerical Optimizer V17 の新機能等を紹介いたします。
1. 分枝限定法前処理部の増強
常に改良を続けている分枝限定法ですが、今回のリリースでは、論理制約に基いた切除平面の追加と制約式の補強ノウハウの導入、解法エンジンとなる単体法のプライシングの改良が主な眼目となります。「ルート問題で既に最適解」という方向により近づき、大規模問題の対応力が高まっています。
2. 厳密解法と wcsp ヒューリスティクスの融合
Numerical Optimizer にはシフトスケジューリングや時間割などの離散計画問題に大きな強みを発揮する wcsp というヒューリスティクスと分枝限定法による厳密解法を備えておりましたが、解法エンジンとしては独立なもので、ユーザーからの呼び分けが必要でした。V17 からヒューリスティクスアルゴリズム wcsp を、連続変数を含む問題に適用することができるようになりました。その際には分枝限定法ならではの、論理制約に着目した強力な前処理が適用されるので、以前の wcsp が苦手としていた論理制約が解空間を狭くしているケースへの対処が可能です。分枝限定法からも以前の単体法ベースのヒューリスティクスに加えて wcsp が起動されるようになり、大規模問題に対する解の探索力が向上、実務的な難問により強力にアプローチします。
3. 行列表現を用いない内点法
最近の研究で内点法のステップ方向ベクトルを求める際に現れる行列に対する理解が進み、その成果としてソルバーに制約式行列を入力しなくても、制約式行列とベクトルの積を計算するインタフェースがあれば機能する内点法を実装しました。行列がメモリに乗りきらない大規模ネットワークや分布の制御など、数値的な性質よりも規模が問題となる超大規模な線形計画問題に福音となる新技術です。ご期待ください。
4. 入力インタフェース強化
より手軽にお試しになりたい方へ、モデリング言語 SIMPLE を介さずにスタンダードな LP ファイルからの入力インタフェースや、セパレータを半角スペースとする拡張された MPS ファイルからの入力インタフェースを用意しました。 併せて SIMPLE で表現したモデルから LP ファイルを出力する機能も追加しました。
SIMPLE:
Variable x;
IntegerVariable y;
Objective obj(type = minimize);
obj = 180 * x + 160 * y;
6 * x + y >= 12;
4 * x + 6 * y >= 24;
0 <= x <= 5;
0 <= y <= 5;
lpout(); // LP ファイル作成
LP ファイル:
MIN
obj : 180 X1 + 160 X2
SUBJECT TO
F1 : 6 X1 + X2 >= 12
F2 : 4 X1 + 6 X2 >= 24
BOUNDS
X1 <= 5
X2 <= 5
GENERALS
X2
END
Numerical Optimizer V16 の更新情報
Numerical Optimizer V16 の新機能等を紹介いたします。
1. 新スケーリングによる安定化
制約式や変数のオーダーを揃えるスケーリング処置のアルゴリズムを改変、問題の性質が未知の状況でもより安定な数値的性能を発揮します。
2. 分枝限定法の改良
変数の前処理ルーチンを改善し、整数性の強い問題でのパフォーマンスを改善しました。
3. WCSP 高速化
大規模離散最適化のためのアルゴリズム WCSP が実務的な大規模問題で 2 倍以上高速化しました。 同じ時間内でより広範囲な探索を行う、より最適性を追求することが可能です。
4. プラットフォーム増強
Windows8 と VisualStudio2012 に対応し、Numerical Optimizer を最新のプラットフォームで動作させることができます。 R 接続した派生製品である RNUOPT は R の V3.0 に対応しています。
※ 対応したのは Windows8 であり、Windows8.1 には対応しておりません。
NUOPT V15 の更新情報
1. wcsp の並列化
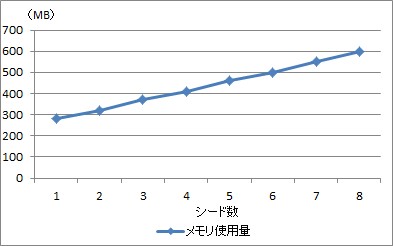
シード毎にコアを割りあてて計算し、最良のものを出力します。 複数シードによる実行が必要な問題については、コア数によってパフォーマンスが向上します。
次のグラフは、ある問題を wcsp でコア数 4(ハイパースレッディングにより 8 に見える)マシンを用いて解いた結果を表しています。 実行するシード数を増やした際の実時間の増加やメモリ使用量の増加率が抑えられていることがわかります。
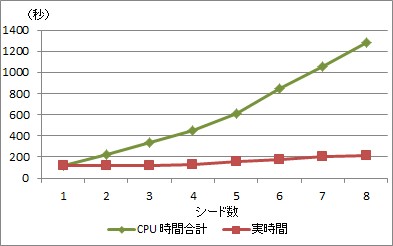
2. python との接続
python から LP/QP/MILP/MIQP を解くインタフェースを用意しました。 NUOPT のライセンスをお持ちの方は、python インタプリタ環境から手軽に NUOPT を実行頂けます。
3. Web アプリ作成
ブラウザを通じて最適化モデルを実行する Web アプリケーションが、GUI 操作のみで手軽に作成できるようになります。
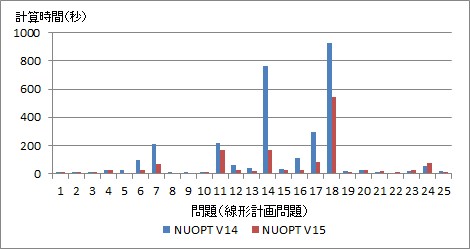
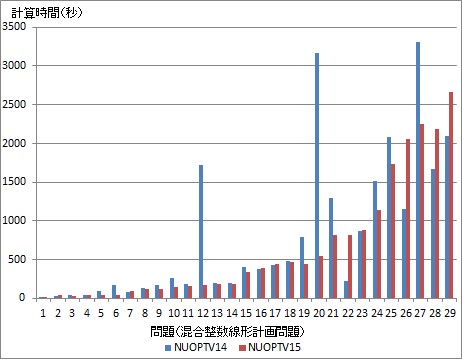
4. 内点法、分枝限定法のスピードアップ
内点法は高速なライブラリの利用、分枝限定法は計算手順の工夫により、問題によっては 30% ~ 50% 以上の高速化が実現できました。 次の図は、線形計画問題・混合整数線形計画問題のベンチマーク問題を NUOPT V14 と NUOPT V15 それぞれで解いた際の計算時間の比較となります。
5. SIMPLE の改良
モデリング言語 SIMPLE の機能をユーザー様の声に従って、一部増強し使い勝手を向上しています。
NUOPT V14 の更新情報
1. マルチコア環境を活かした分枝限定法の並列化
整数計画問題に対する分枝限定法エンジンに、マルチコア環境を活かした並列化オプションを導入しました。
2. 新しい非線形最適化アルゴリズムの実装
ペナルティ関数を用いない、新しい非線形最適化のアルゴリズム SLPSQP が導入されました。 有効な制約を仮定して計算を進めるという性質上、問題によっては NUOPT の内点法よりも高精度で解が求まります。 内点法の解と結果を比較して解の一意性を確認するなどのご利用も可能です。
3. モデリング言語 SIMPLE の機能追加
for 文を使わず、漸化式を用いた値の定義が可能になりました。 値を評価する部分の省メモリ化・高速化もあわせて達成されています。
4. GUI の刷新
Excel との連携機能など操作感はそのまま、実装を刷新し、 (株)数理システムのマイニングツール Visual Mining Studio や金融工学支援ツール FIOPT と共通のプラットフォーム Visual Analytics Platform(略称 VAP)上で動作するようになりました。 グラフ描画が強化、データハンドリングのための機能も追加されています。
NUOPT V13 の更新情報
1. Matrix/Vector クラスの導入
モデリング言語 SIMPLE のクラスとして行列・ベクトルを直接記述するための Matrix/Vector クラスを導入します。 標準形の LP やその双対表現をコンパクトに記述、操作することが可能になります。 例題集にも、二次割当問題や MAX-CUT 問題など、行列・ベクトルを利用する例を追加します。
標準形の LP とその双対問題の記述
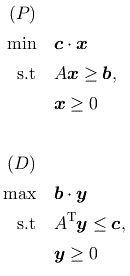
Set M, N;
Element m( set = M ), n( set = N );
Matrix A(( m, n ));
Vector b( m ), c( n );
Variable x_var( index = n ), y_var( index = m );
Vector x( n ), y( m );
x[n] = x_var[n]; // 変数 x をベクトルに詰める
y[m] = y_var[m]; // 変数 y をベクトルに詰める
// Primal
Objective f( type = minimize );
f = inprod( c, x );
A*x >= b;
x >= 0;
// Dual
Objective g( type = maximize );
g = inprod( b, y );
trans(A)*y <= c;
y >= 0;
2. SIMPLE の速度向上
モデリング言語 SIMPLE の一部実装の刷新により、大規模な数式の解釈の速度が飛躍的に向上します。以下のテーブルは、大きさ n の集合の要素 5 個を添字として持つパラメータの和の計算時間を V12、V13 で比較したものです。
| n (n5) | 8 (32,768) | 10 (100,000) | 12 (248,832) |
|---|---|---|---|
| V12 | 2.9 秒 | 22.3 秒 | 212.3 秒 |
| V13 | 0.7 秒 | 2.2 秒 | 4.9 秒 |
3. 混合整数計画問題の速度向上
混合整数線形・二次計画問題における分枝限定法が、V12 での進化に留まらず、さらに改善します。最適化計算の前処理ルーチンの強化により、問題全体で見て速度が向上しています。
4. マニュアルの充実
Excel 連係に関連するマニュアルを一本化致します。以前は「Excel 連係チュートリアル」と「Excel 連係マニュアル」の二種類のマニュアルが存在しましたが、これらを「NUOPT/SIMPLE/Excel 連係マニュアル」として一本化し、解説を充実致します。
また、好評をいただいておりますチュートリアル内の「例題集」部分を独立させ、新たに「NUOPT/SIMPLE 例題集」と致します。新たな数理計画問題の例題として「包絡分析法(DEA) モデル」「巡回セールスマン問題」「ロジスティック回帰モデル」、さらに NUOPT V13 より新たに導入される Vector/Matrix クラスを利用した「最大カット問題」「二次割当問題」を追加いたします。
5. マニュアル参照・検索機能の向上
NUOPT V13 では、各マニュアルの内容をスタートメニューから参照する事が可能になります。用語をキーワード検索する事も可能です。ユーザー様の利便性向上の一助となれば幸いです。
6. 外部 CLAPACK のリンク機能
ユーザー様がお持ちの CLAPACK を NUOPT ライブラリへリンクすることができるようになります。これにより大規模な線形計画問題において内点法を用いる場合の求解速度が速くなる場合があります。 例えば、Intel 社の MKL を使用することで、CPU が Core2 Quad 3GHz(Q9650)で求解時間が 1/3 となった問題がありました(*1)。
(*1)これは結果の一例であり、全ての問題で必ず同程度速度が速くなることを保証できるわけではありません。しかしながら、MKLの場合はスレッド化されるため、Many Coreの環境では多くの問題でより高パフォーマンスとなることが期待できます。
NUOPT V12 の更新情報
<<お知らせ>>
- NUOPT V12 の価格・製品ラインナップにつきましては 資料請求・お問い合わせ よりお問い合わせください。
- NUOPT V11 をもちまして Borland C++ 5.5 への対応を終了させていただきます。 御案内につきましては Nuorium Optimizer 対応機種/OS に掲載しております。
- NUOPT V12.1.0 をお持ちで Microsoft Visual Studio 2010 をコンパイラとしてご利用になりたいお客様は 資料請求・お問い合わせ よりお問い合わせください。
1. 非線形計画問題におけるパフォーマンスの向上
一般の非線形最適化問題に対するアルゴリズムである、信頼領域に基づく 内点法 / 外点法 の性能を向上させました。 信頼領域法 では、解近傍で超一次収束させるためのニュートン方向と、 解から離れている場合にも 大域的な収束性 を保証するための降下方向の二つの方向を適宜用いて反復計算を行いますが、 降下方向に ヘッセ行列 の固有値などの、より現実的な問題の情報を反映させることで 特に難しい問題に対するパフォーマンスを向上しました。 さらに、一般に有効なスケーリングが難しいと言われている一般の非線形最適化問題に対する スケーリング手法 を開発、チューニングの結果、産業界で現れる実際的な問題に対する全般的な性能を向上させました。 特に良い初期解が得られないケースで、その効果は顕著に現れます。 その結果、反復の停止条件を 1.0e-8 と以前に比べて 2 桁程度厳しくしているにもかかわらず、 非線形計画問題に関する ベンチマーク問題 CUTE 459問について、 ほぼ 9割の404 問について全くチューニングせずに 局所的な最適解 を得ることに成功しています。
2. メモリマネジメントの機能増強
権限の低いユーザ環境においても最大使用メモリ量の設定を行えるようになりました。
3. 整数計画問題に対する分枝限定法の改善
最新のヒューリスティクス ( diving、feasibility pump、etc..)及び 切除平面 (Gomory Mixed Integer cut、 Mixed Integer Rounding cut)の技術を導入することにより、 整数計画問題に対する 分枝限定法 の性能が改善されました。 特に 実行可能解 を見つける速度が向上し、得られる 実行可能解 の質も大幅に改善されています。 V12 では MIPLIB3 の問題で、65 問中 17 問の問題で速度の改善がされました。 次のグラフは、MIPLIB3 の一部(arki001、danoint、mkc、swath、dano3mip、fast0507、set1ch)を除いた問題に対する NUOPT V11 と V12 の計算時間の速度比較です。縦軸が各問題、横軸が計算時間(秒)になっています。
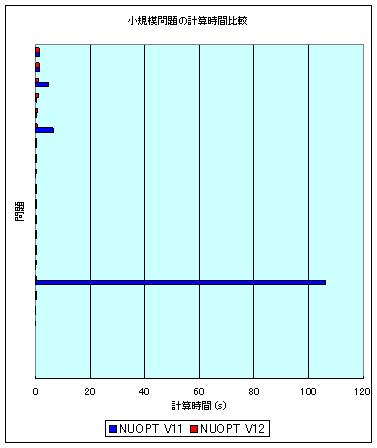
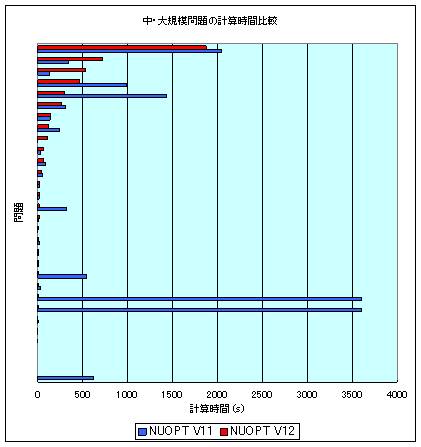
また今回導入される技術は、発電計画から広告配信まで幅広いジャンルに対して威力を発揮します。是非ご利用ください。
4. Mac 版発売
兼ねてからご要望が多数ありました Mac 版 NUOPT を新発売いたします。 対応の環境は Intel プロセッサ搭載の Snow Leopard となっております。 Windows で標準搭載されている GUI は対応予定はございませんが、コアの計算部分については当然 Windows 版 UNIX 版 Linux 版 と等価なものとなります。 ご興味がある方は是非ともお問い合わせください。
5. 最新の開発環境への対応
NUOPT V12 より Windows 7 に対応いたしました【注】。 また、Windows 版において最新の開発環境である、Microsoft Visual Studio 2010 に NUOPT V12.1.5 より対応いたしました。 なお過去のコンパイラ(.NET2003、VS2005、VC6)もサポートしておりますので過去の資源も無駄になりません。 【注】一部機能(GUI のプロジェクトボードにドラッグされた .csv ファイルのビュー)をご利用頂けません。
NUOPT V11 の更新情報
<<お知らせ>> NUOPT V11 の価格・製品ラインナップにつきましては 資料請求・お問い合わせ よりお問い合わせください。
1. DFO による求解アルゴリズムの導入(アドオン機能)
DFO(derivative free optimization)の手法を用いた求解アルゴリズムを導入致します。 このアルゴリズムはシミュレーション等によって求まるような、数式では記述できないシステムに対して最適化計算を行うことが出来るようになります。 また、通常の制約式と合わせて用いることができ、幅広い問題をサポートします。
(注意)現段階では以下の問題には対応しておりませんのでご了承ください。
- 整数変数・離散変数を含む問題
- 微分不可能である制約条件を含む問題
また、本機能は NUOPT 本体 NLP モジュールもしくはフルセットをお持ちの方向けの有償アドオンとして提供致します。 なお、MP.doc は本機能に対応しておりませんのでご了承ください。
2. 内点法/外点法機能増強
NUOPT の内点法/外点法アルゴリズムはメリット関数を用いた大域的収束の保証、二階微係数の情報を活かした優れた局所的収束性を備えています。 V11 では大規模な非線形計画問題で特に数値的な性質の悪い問題に対する頑健性を増す方策を実装しました。 ベンチマークの結果から見ても安定性、高速性は世界最高レベルです。
3. 制約充足アルゴリズム(WCSP)用の関数のさらなる追加
V10 で導入した max/min 関数に加え、V11 ではさらに argmax/argmin、count 関数を追加します。 最大値をとる式番号を取得したり、線形の制約式を充足している個数を取ったりするような定式化困難な問題に対し、中間変数の導入なしで簡便なモデル記述と性能の大幅な向上を可能にします。 今回導入された関数は設備計画・エネルギー問題・金融・広告配信等様々なジャンルに対して威力を発揮できるものです。
4. 信頼領域法を利用した、非線形半正定値計画問題に対する内点法
非線形半正定値計画問題に対して、信頼領域法のアイデアを利用した内点法が導入されます。 V10 で導入された準ニュートン法を用いる方法に比べて安定性が向上し、より規模の大きな問題が取り扱えます。
「通常の非線形制約 + 線形の行列制約」というタイプの問題に対して一定のパフォーマンスが得られる事が確認されています。 半正定値制約を課す行列の成分に、非線形項が出現する問題も取り扱う事ができます。しかしながら、このタイプの問題群に対してはパラメータチューニングが必要で、性能は問題に依存します。
具体的な問題をお持ちの方は、資料請求・お問い合わせ までご相談ください。
5. 最新の開発環境への対応
Windows 版において最新の開発環境である Microsoft Visual Studio 2008 に対応します。 Microsoft より無償で提供されている Express Edition にも対応しているため安価に最新の コンパイラの性能を享受することができます。 なお、過去のコンパイラ(VC++6、.NET2003、VS2005、BorlandC++5.5)も変わらずサポート する予定ですので、過去の資産も無駄になりません。
NUOPT V10 の更新情報
<<お知らせ>>
旧バージョンをご利用で保守に加入されている方につきましてはバージョンアップのお取り扱いは 以下のようになります。
- 旧バージョンの LP/IP モジュールをお使いの方
NUOPT V10 では LP/IP Lite モジュール・LP/IP モジュールのいずれかをお選び頂きます。(次年度以降の保守料金はお選び頂いたモジュールの料金が適用されます。) - 旧バージョンの NLP モジュールをお使いの方
NUOPT V10 では NLP モジュール・フルセットのいずれかをお選び頂きます。(次年度以降の保守料金はお選び頂いたモジュールの料金が適用されます。)
1. 非線形半正定値計画問題 (SDP) 用の求解アルゴリズムの導入
一般の非線形最適化問題に半正定値性制約を導入した問題を扱うことができます。半正定値性制約の対象となる行列の要素や、目的関数・制約式に非線形関数を用いることができるのが大きな特徴です。モデリング言語 SIMPLE に新しく導入された SymmetricMatrix クラスを用いて半正定値制約を記述することによって、問題を簡便かつ汎用的に記述することができます。この記述を利用することにより、相関行列取得問題、ロバストポートフォリオ最適化、二次ロジット関数のフィッティングなど、半正定値性制約付きのアプリケーションへの導入が容易です。
次は、与えられた行列と最も近い正定値な(最小固有値は minEig )相関行列を取得する 問題(nearest correlation matrix problem と呼ばれています)をモデリング言語 SIMPLE に よって記述したものです。
<< 相関行列取得問題の SIMPLE での記述例 >>
Set N; // 行列の各要素
Element i(set=N),j(set=N);
Variable x(index=(i,j));
Parameter a(index=(i,j)); // 与えられた行列の要素
SymmetricMatrix m((i,j));
Parameter minEig; // 出力される相関行列の最小固有値
m[i,i] = 1; // 対角は 1 とする
m[i,j] = x[i,j], i > j; // 下三角部分の定義
m >= minEig; // 半正定値制約
Objective diffnrm(type=minimize); // 差の行列のフロベニウスノルム
diffnrm = sum(pow(x[i,j]-a[i,j],2),(i,j,i < j));
2. 制約充足アルゴリズム(wcsp)用の微分不可能な関数の追加
関数群の最大、最小を求める max/min 関数など、一般の数理計画問題の記述には微分不可能な関数が現れます。例えば max 関数は設備計画問題(最大負荷に耐える機器を選定する)などに頻出します。
通常の定式化では、数理計画法アルゴリズムが微分不可能な関数と整合しないために中間変数を導入して通常の微分可能な形に変換するなどの措置を行っていましたが、問題規模の増大を招く一因となっています。一方メタヒューリスティクスアルゴリズム(wcsp)は微分不可能性を仮定していないので、近傍探索ルーチンの工夫を行えば定式化の変形を行うことなく、効率的な求解が可能です。
V10 では、まず線形な関数群の max/min 関数を自動判別して、メタヒューリスティクスアルゴリズム wcsp での求解を高速化する機能を導入します。この機能の組み込みによって、直観に近い形での簡便なモデル記述と性能の大幅な向上を可能にします。
3. 非線形最適化アルゴリズムの改良
V8 で導入された主双対外点法(lepm,tepm)に関する初期値推定法、パラメータコントロールの最新の研究成果を反映させ、安定化・高速化がなされています。外点法は良い初期値が存在する問題に対して、内点法よりも高速に収束することがいくつかの実験において確かめられています。
4. GUI の改良
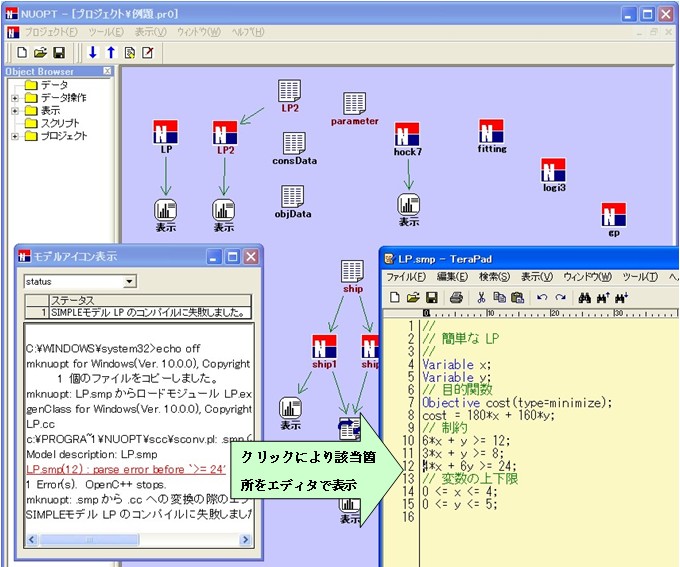
お客様から頂いた声に対応し、NUOPT Windows 版の GUI の操作性を向上させました。メッセージウインドウと経過表示が一体化、エラーメッセージおよびアルゴリズムの実行経過の管理・確認が容易になります。また、エラーメッセージをタグ化、クリックによりモデルの該当箇所がエディタで表示される機能によってモデルのエラー修正も容易になります。
<< NUOPT Windows 版 GUI の新機能 >>
5. チュートリアルの改訂
パッケージに付加している数理計画モデルのサンプル例題集(NUOPT/SIMPLE チュートリアル)を一部改訂、より分かりやすい表現にするほか、以下の例題を増強します。テンプレートや授業等にご活用ください。
<<NUOPT/SIMPLE チュートリアルに追加されるサンプル例題一覧>>
- 格付け推移行列推定問題
- イールドカーブ推定問題
- 相関行列取得問題
- ロバストポートフォリオ最適化問題
- 設備計画問題
6. 商品ラインアップの変更
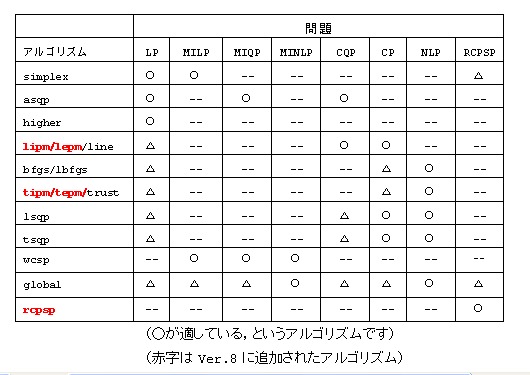
お客様の様々なご利用形態に対応できるよう 4 種類のモジュールをご用意致しました。
<<NUOPT V10 の機能比較表>>
| 問題の種類\ モジュール名 |
LP/IP【1】 | wcsp/rcpsp【2】 | NLP【3】 | Global【4】 |
|---|---|---|---|---|
| LP/IP Liteモジュール | ○ | × | × | × |
| LP/IPモジュール | ○ | ○ | × | × |
| NLPモジュール | ○ | × | ○ | △【5】 |
| フルセット | ○ | ○ | ○ | △【5】 |
【1】(混合整数)線形計画問題の求解に NUOPT を利用する場合
【2】求解の際にメタヒューリスティクス解法(制約充足アルゴリズム・資源制約付きスケジューリングアルゴリズム)を利用する場合
【3】非線形計画問題の求解に NUOPT を利用する場合(NUOPT V10 で導入される半正定値計画問題用の求解アルゴリズムを利用される場合を含みます)
【4】求解の際に大域的最適化アルゴリズムを利用する場合
【5】ご利用の際にはアドオンの NUOPT/Global が必要です
NUOPT 9.2.0 の更新情報
<<お知らせ>>
既に NUOPT9 の正規ライセンスをお持ちの方には、NUOPT9.2.0 を無償でご提供します。 具体的な取得方法は、資料請求・お問い合わせ よりお問い合わせください。
その際は、
- 正規ライセンスのご登録者名
- シリアル番号
- 正規ライセンスのご登録者のご連絡先(電話番号またはメールアドレス)
を必ずお伝えください。これらの情報がない場合、ご提供にお時間を頂く場合がございます。 インストール方法の詳細は NUOPT9.2.0 に付属のインストールマニュアルをご覧ください。
1. 対応 OS に Windows Vista を追加
Windows2000、XP に加え、Windows Vista 上でも動作するようになりました。
2. デフォルトのプロジェクト領域のフォルダを変更
プロジェクト領域のフォルダーを NUOPT のインストールフォルダー以下から APPDATA(*1) フォルダー以下に移動しました。
(*1) APPDATAフォルダーとは、Windows の各バージョンにより次の場所を指します。
- 2000 : C:\Documents and Settings[ログオン名]\Application Data
- XP : C:\Documents and Settings[ログオン名]\Application Data
- Vista : C:\Users[ログオン名]\AppData
3. NUOPT のインストールフォルダー以下の書き込み権限が不要
NUOPT9 以前では、NUOPT のインストールフォルダー以下に書き込み権限が必要でした。 NUOPT9.2.0 からはインストールフォルダー以下に書き込み権限が不要になりました (*2)。
(*2) NUOPT9.2.0 を新規にインストールした場合に限ります。 古い NUOPT から NUOPT9.2.0 へのアップグレードのインストールでは、インストールフォルダー以下に書き込み権限が必要となりますのでご注意ください。 この場合は、古い NUOPT をアンインストール後に NUOPT9.2.0 をインストールすることで、 書き込み権限が不要になります。
4. GUI から起動されるデフォルトのテキストエディタを TeraPad に変更
NUOPT9 以前では、デフォルトのテキストエディタは Windows に付属の「メモ帳」でした。 NUOPT9.2.0 からは、「TeraPad」というフリーなテキストエディタを同梱し、これをデフォルトの テキストエディタとしています(*3)。
(*3) TeraPad は、作者である 寺尾 進 氏のご好意により、同梱することが できました。 TeraPad の詳細は、寺尾氏のホームページをご覧ください。
5. 「グラフ表示」アイコンの削除
NUOPT9 以前には「グラフ表示」アイコンにより結果をグラフ表示することができましたが、 NUOPT9.2.0 以降はこの機能をサポートしなくなりました。 古い NUOPT で「グラフ表示」アイコンを使用していたプロジェクトを NUOPT9.2.0 でインポート することはできますが、グラフ表示はできないようになっています。
6. 共通フォルダーの削除
NUOPT9 以前にはプロジェクトを共通フォルダーに格納することで、全ユーザでプロジェクトを 共有できました。 NUOPT9.2.0 以降はこの機能をサポートしなくなりました。
7. 最新の NUOPT ライブラリの同梱
NUOPT9 に同梱されていた NUOPT のライブラリ(9.1.0)より、いくつかのバグフィックスを 施しております。なお、バグフィックスの詳細につきましては Nuorium Optimizer 累積修正パッチ をご覧ください。
NUOPT 9 の更新情報
<<お知らせ>>
- 2007 年 9 月 18 日より NUOPT 9.2.0 (Windows Vista 対応版) の提供を開始いたしました。
- 2007 年 1 月以降に
- 新規に NUOPT 8 をご購入頂いた方
- 旧バージョンからの有償バージョンアップのお申し込みを頂いた方
は NUOPT 9 へ無償でバージョンアップ致します。
1. 資源制約付きスケジューリングアルゴリズム(rcpsp)にリスケジューリング機能搭載
メタヒューリスティクス解法の一つであるタブー・サーチを用いたエンジン rcpsp に新機能を搭載します。
それは「ある日突然人が来られなくなった」「機械が故障してしまった」などの突発的な 出来事にも対応出来る、リスケジューリング機能です。 また、初期値設定や、リスタート機能、ガントチャートのリスケジューリング対応等 の従来の機能もより増強致しました。より現実的なスケジューリングを お考えの方、これを機に導入を考えてみてはいかがでしょうか。
<<リスケジューリングイメージ図>>
2. 制約充足アルゴリズム(wcsp)の新機能 ペナルティの表示・「セミ・ハード」制約の追加
wcsp による制約充足問題の求解結果において、解におけるペナルティ値を一覧表示する機能を搭載します。適切に定式化したつもりなのにハード制約が残ってしまう場合の強力なデバッグ手段となるほか、ソフト制約の重みの設定の調整においても役立ちます(出力例をご参照ください)。
また、制約種別に「セミ・ハード」が追加されました。これまではハード制約はすべて等価であったため、問題が実行不可能な場合には問題の根本的な制約を満たせない解が出力されてしまいました。 Ver.9 からは、実行不可能性を「押しつける」先を「セミ・ハード」制約として定義すれば、問題が実行不可能な場合でも、出力から有効な情報を得ることができます。
<<出力例>>
%%
%% WCSP_PENALTY
%%
NAME TYPE VALUE BOUND AMOUNT WEIGHT PENALTY
F# 245 nurse.smp:314[6] HARD 0 >= 1 1
F# 432 nurse.smp:321[13] HARD 0 >= 1 1
F# 5281 nurse.smp:348[26,18] HARD 3 <= 2 1
F# 9728 nurse.smp:366[18,28] S.HARD 2 <= 1 1
F# 10161 nurse.smp:368[1,17] S.HARD 2 <= 1 1
F# 3 dayCons0[4] SOFT 9 >= 10 1 1 1
F# 8 dayCons0[9] SOFT 9 >= 10 1 1 1
F# 11 dayCons0[12] SOFT 9 >= 10 1 1 1
F# 17 dayCons0[18] SOFT 9 >= 10 1 1 1
F# 8170 nurse.smp:358[16,26] SOFT 3 <= 2 1 10 10
F# 8231 nurse.smp:361[2,13] SOFT 0 == 10 10 1 10
F# 8235 nurse.smp:361[10,16] SOFT 0 == 10 10 1 10
F# 8305 nurse.smp:362[24,26] SOFT 0 == 10 10 1 10
3. 誤差関数の組み込み
かねてからご要望の多かったガウスの誤差関数 erf(x) を SIMPLE で扱えるよ うになりました。分布を仮定した判別分析や確率計画などの用途に役立ちます。
4. マニュアルの全面改訂
マニュアルの全面改訂を行います。
NUOPT/SIMPLE マニュアルは、ユーザー様からいただいた様々なご意見・ご要望を反映させ、 よりコンパクトで実用的なものに改訂します。また、 NUOPT/SIMPLE チュートリアル には、様々な数理計画モデルのサンプル例題を追加します。テンプレートや授業等に ご活用ください。
<<NUOPT/SIMPLE チュートリアルに含まれるサンプル例題一覧>>
- 配合問題
- 輸送問題
- 多期間計画問題
- ナップサック問題
- 集合被覆問題
- 最大流問題
- 最小費用流問題
- 多品種流問題
- pメディアン問題
- pセンター問題
- 割り当て問題
- 最小二乗問題
- ポートフォリオ最適化問題
- ジョブショップスケジューリング問題
5. 最新の開発環境への対応
最新の開発環境である Microsoft Visual Studio 2005(以下、VS2005)に対応します。 また、Windows XP x64 と VS2005 の組み合わせでは、64bit での開発が可能となり、 より大規模な問題にも対応できます。
NUOPT 8 の更新情報
1. 資源制約付きスケジューリングアルゴリズム(rcpsp)
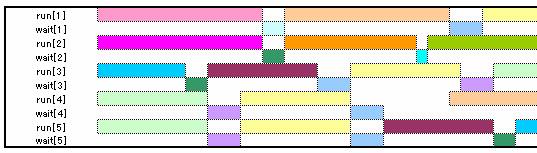
メタヒューリスティクス解法の一つであるタブー・サーチを用いて資源制約付きスケジューリング問題を解くエンジンです。人・予算・資金などの枠の中で与えられたタスクを処理するタイミングを決定するスケジューリング問題にあまねく適用可能です。ジョブショップスケジューリングはもちろん、複数要員へのタスクのアサイン、納期遅れの最小化などに、高速に良質の実行可能解を与えます。
問題記述はすべてモデリング言語SIMPLEより与えることができますので現場で現れるような一種複雑な制約も柔軟に記述できます。SIMPLEによる記述方法のチュートリアルが付属していますので初めての方でも容易にお使いになることができます。
Excel連係と rcpsp を併用すると、ガントチャートを出力させる事ができます。以下は、ガントチャートの一例です。
2. 非線形最適化アルゴリズムの改良
非線形最適化に適した内点法アルゴリズム(lipm,tipm)を変更し、実装のチューニングによって、数値的に難しい(非凸性が強い)問題に対する安定性がVer.7に比べて向上しました。また、良い初期値が存在する問題について、高速に収束するなどの好ましい性質を持つ主双対外点法(lepm,tepm)が追加されました。
3. 実行不可能性検出機能
数理計画問題の作成において困難なことのひとつが実行不可能エラーの回避です。Ver.8からは、ユーザ支援機能として、実行不可能性の原因抽出機能(iisDetect)を標準実装しました。iisDetectは
Variable x,y,z;
Objective f(type=minimize);
f = x + y + z;
x >= y ; // IIS
1 + z >= x ; // IIS
y >= 2 + z; // IIS
x + y + z >= 0;
のように互いに矛盾をはらんだ問題の制約式の組(Irreducible Infeasible Set:IIS)を発見し、解ファイルに次のようにレポートします。
%%
%% IIS
%%
-----------------------------------------------------------------------------
#2 lp.smp:4 : y - x
<= 0 ( 0)
-----------------------------------------------------------------------------
#3 lp.smp:5 : -1 + x - z
<= 0 ( 0)
-----------------------------------------------------------------------------
#4 lp.smp:6 INFS : 2 + z - y
<= 0 ( 1)
実行不可能性の原因はこのようにレポートされたIISの組に集約されているのでユーザーは実行不可能性の原因をたどりやすくなります。ここで、実行不可能性に無関係な7行目の制約式はレポートに現れていないことにご注意ください。
4. 大域的最適化機能の改良
緩和問題を二次計画問題に改良することによりさらに安定化、高速化しました。実行可能解は得られているが、最適性の保証ができていないケースの解析、ローカルな最適解に落ちてしまいやすい問題に威力を発揮します。
5. その他コンサルティングサービス、パッケージアプリケーションのご紹介
(株)数理システムは導入と応用例についてのノウハウをあわせたサービスも提供いたします。数理計画の実務経験豊富なスタッフがあなたの問題にアプローチし、コンサルテーションからインタフェース作成まで総合的にサポートします。
NUOPT を用いたソリューション・コンサルテーションをあわせて提供する、次のようなパッケージ製品もご用意しております。
- Visio とExcelを用いた運転計画モデラー(SCHOpt)
- WordとExcelを用いたモデル化ツール(MP.doc)
- (NEW!)資産リスクシミュレーション・最適化ツール(Risk PRIMER)
- (NEW!)シフトスケジュール作成ツール
NUOPT 7 の更新情報
1. 制約充足アルゴリズム(wcsp)
配車スケジューリング、人員配置、作業分担表作成、時間割作成など、現実の場面において何らかの「マス目を埋める」というタイプの計画を立てねばならないという機会は数多くあります。我々は安価で高性能な計算機環境を手にしていますが、計算機の力を十分に活かして計画業務を行うことができているでしょうか。計算機を利用しているといっても多くの場合、計画そのものは手作業や勘で行って、計算機はその作業の過程や結果を記録、印刷、あるいは送付するのみとなってしまうのが殆どではないでしょうか。
膨大なパワーを持つ計算機をより活用して、計画そのものを改善してみませんか。NUOPTの新機能である制約充足アルゴリズム(wcsp)を使えばそのような計画業務を計算機によって比較的簡便にかつ高速に行わせることができます。
この制約充足アルゴリズムは、実務的な要件を入れることによって複雑化した式にも適用することができます。整数変数のみからなる問題であれば制約式や目的関数の記述に制限はありません。NUOPT付属のモデリング言語SIMPLEの柔軟な記述性の良さを十分に活かすことができます。適当に制約式を並べてゆくと、相反して両立しない制約が現れるものですが、そのような場合でもこのアルゴリズムは制約をできるだけ満たす解を求めてくれます。レスポンスも早いので、制約式の追加や消去などを対話的、かつ柔軟にモデリングしてゆくという、ある意味贅沢な使い方も可能です。このアルゴリズムは京都大学「問題解決エンジン」グループの開発によるもので、汎用性と高速性において世界でもトップレベルにあります。
NUOPTを用いて、より高度な計画業務を行ってみませんか。具体的なアプリケーションへの適用やモデル記述についてもご相談ください。
2. 大域的最適化機能(NUOPT/Global)
NUOPTには既に非線形最適化機能が備わっておりますが、解析的な性質が明らかでない非線形最適化問題に適用した場合、その出力は局所的最適解ではあっても大域的最適解であるという保証はありません。従って、例えば初期値を変更すると異なる解が出力されるなどの現象が起きます。また、整数変数を含む非線形最適化は行うことができません。
NUOPT/Globalは非線形計画問題を大域的に(厳密に)解きたいという要請に応えます。非線形計画問題が整数変数を含んでいても大丈夫。モデリング言語によって記述された式を解釈し、自動的に凸緩和法を適用するので、最適解の上下限を知ることも可能です。
※ 大域的最適化アルゴリズムは LP/IP モジュール並びに NLP モジュールには対応しておりません。実行に際しては有償アドオン NUOPT/Global の別途購入が必要となります。 価格については 資料請求・お問い合わせ よりお問い合わせください。
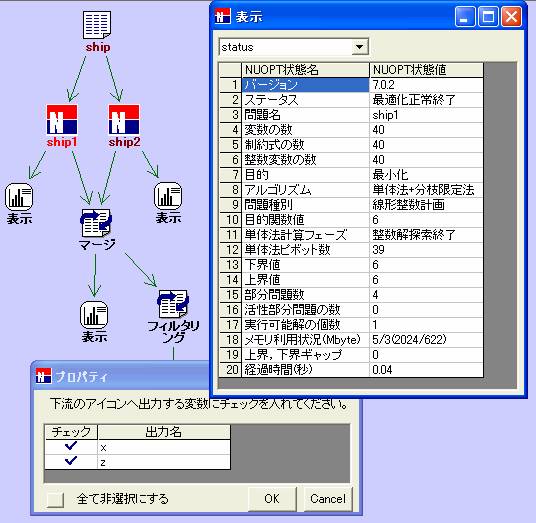
3. GUI機能およびマニュアルの充実
モデルとデータの結合を示すのみならず、入出力データの加工もビジュアルに示すことができるNUOPT GUIがブラッシュアップし、より高速で快適な操作感を実現しました。マニュアルのラインアップも刷新、PDFフォーマットにより配布しますので、検索も容易です。
NUOPT 6 の更新情報
1. GUI 部分(Windows版のみ)
Ver.6ではユーザの方々の声を取り入れ、より使いやすく機能アップしました。 GUI を通してしかアクセスできなかったファイルを外で編集したり閲覧したりできるようになったことが大きな変更です。
1.1. モデル、データファイルの扱い(外部のエディタの起動)
モデル(.smp)とデータ(.dat/.csv)アイコンの実体はユーザの管理する任意のディスクスペース上にあるものとし、ユーザの編集がその都度反映されるようになりました。Ver.5ではモデル、データをエクスプローラからGUIのボードにドラッグ&ドロップすると、その都度GUI内にコピーが生成されるので、ユーザがエクスプローラ上に作成したモデル、データを変更してもその変更がGUIには反映されず、GUIが提供する手段でしかモデルやデータの編集ができませんでした。Ver.6ではモデル、データファイルをドラッグ&ドロップしても、GUIはコピーではなく、ファイルをリンクとして認識します(各アイコンはオリジナルのファイルの絶対パスを記憶します)。そのため、モデルやデータファイルを任意のエディタで編集し、その都度最適化に反映させることができます。
GUIからモデル、データの編集メニューを押した際には外部のエディタプログラム(デフォルトは「メモ帳」)が立ち上がります。これによって、Ver.5で問題となっていたモデルやデータの編集画面がボードに重なって作業がしずらくなることも避けられます。またエディタプログラムをユーザが指定することも可能です。 Ver.5のモデル、データ編集エディタには印刷という機能がありませんでしたが、Ver.6では外部エディタを通じて、印刷が可能になります。
1.2. 外部環境との親和性
Ver.5では最適化の結果を見るにはNUOPTGUIをいったん通す必要がありましたが、Ver.6では、最適化を行うと、その関連付け先のモデルファイルのあるフォルダに result という名前のフォルダを作成してそこに結果がまとめて格納されるようになりました。
さらに、デバッグ用やテスト実行のためにExcel連携を行った場合のExcelからの内容と等価なデータファイル(.dat)がモデルファイルのあるフォルダに excel.dat という名前で作成されるようになりました。また、モデルに対応する実行モジュールもモデルファイルのあるフォルダにコピーされます。
1.3. グラフ機能追加
NUOPTGUI固有のツールとしてグラフを描くアイコンが追加され、Excelを経由せずとも計算結果をグラフ表示することができるようになりました。「NUOPTWindows版マニュアル」の「1.13.7 NUOPTグラフ描画機能によるグラフ描画」にその具体例がございます。
2. モデリング言語部分
数理計画問題を記述する付属のモデリング言語SIMPLEの機能改良です。 特にエラーチェックまわりが充実しました。浮動小数点エラーやデー タファイルのエラー、その他の実行時エラーもモデル記述の行番号で特定でき るようになりましたので、モデルのデバッグが容易になります。ユーザー支援に関する機能が増強されています。
2.1. エラー出力の強化
Ver.6より、モデルやデータファイルにエラーがあった場合、エラーメッセージとともにエラーの検出された行番号を出力するようになり、デバッグが容易になりました。Ver.5では変数やパラメータ利用の場所が宣言の場所よりも先に現れている場合のエラーが別のエラーに見えるという不具合がありましたが、それについても修正しています。
2.2. データの上書き
Ver.5よりパフォーマンスの下落を防ぐため、同一の名前のオブジェクトをデータファイルから複数回定義することを禁止しておりますが、Ver.6ではその扱いを緩め、
options.multDataPolicy = 1;とすると、許すようになりました。詳細は「SIMPLEマニュアル」の「7.3 データ名の重複について」をご覧ください。
2.3. 浮動小数点エラーの検出
非線形最適化の実行時、ゼロ割やオーバーフローが起きた場合に、原因をモデリング言語の行番号単位で追跡して表示する機能が追加されました。
2.4. アンチウイルスソフトとの並存による不具合の解消
Ver.5ではアンチウイルスソフトがリアルタイムディスク保護を行っている場合、大規模な問題においてモデリング言語の解釈速度が低下するという問題がございました。Ver.6ではNUOPT側でこの対策を講じ解決されております。このため、場合によっては数倍程度の実行速度の向上が得られます。
3. 数理計画アルゴリズム本体部分
NUOPT本体のライブラリ部分に対する機能強化について説明します。
3.1. 非線形計画法に対する逐次二次計画法(SQP法)の導入
内点法に加えて逐次二次計画(Sequential Quadratic Programming:SQP)法が組み込まれました。SQP法は非線形計画問題の解法の一つとしてよく知られていますが、今回組み込んだSQP法は、大規模問題におけるパフォーマンスを考慮した数理システム独自のアルゴリズムに基づくものです。その実装においては大規模問題に対する単体法・有効制約法・内点法において弊社が培ったノウハウが注入されております。数値実験の結果、既存の内点法と同等の安定性を備えていることが確認され、一部の問題では内点法よりも安定かつ高速に解を求めることができます。
変数および制約式数がいずれも3000個以下の非線形計画問題421問(ベンチマーク問題集CUTEより選択)中、内点法のみで解けるのは359問(85%)でしたが、SQP法を解法の選択肢として加えると、388問(92%)を解くことができるようになりました。
3.2. 整数計画法の高速化
Ver.6では混合整数計画問題の実行速度が大幅に改善しました。以下は混合整数線形計画問題の実験例です。
| 問題 | #変数 | #制約式 | #整数変数 | Ver.6(秒) | Ver.5(秒) | 倍率 |
|---|---|---|---|---|---|---|
| MIP1 | 124 | 133 | 71 | 38.4 | 89.7 | 2.3 |
| MIP2 | 504 | 1541 | 1417 | 7.1 | 12.2 | 1.7 |
| MIP3 | 1225 | 1152 | 672 | 6.4 | 11.5 | 1.8 |
| MIP4 | 98 | 1989 | 1989 | 11.4 | 13.3 | 1.2 |
| MIP5 | 106 | 117 | 64 | 76.3 | 482.1 | 6.3 |
| MIP6 | 92 | 104 | 58 | 8.6 | 34.8 | 4 |
| MIP7 | 213 | 260 | 259 | 86.6 | 139.8 | 1.6 |
| MIP8 | 292 | 556 | 315 | 200.2 | 642.1 | 3.2 |
| MIP9 | 2055 | 10724 | 10724 | 146.3 | 1027.9 | 7.0 |
| MIP10 | 332 | 45 | 45 | 39.8 | 85.3 | 2.1 |
| MIP11 | 144 | 572 | 572 | 2.5 | 13.7 | 5.5 |
| MIP12 | 1393 | 1224 | 408 | 112 | 251.9 | 2.2 |
| MIP13 | 1369 | 1152 | 384 | 8.2 | 10.8 | 1.3 |
| MIP14 | 37 | 87482 | 87482 | 44.3 | 258.9 | 5.8 |
| MIP15 | 1193 | 840 | 48 | 397.2 | 1566.5 | 3.9 |
| MIP16 | 457 | 1541 | 1417 | 3.6 | 10.8 | 3.0 |
| MIP17 | 364 | 1298 | 1254 | 31.8 | 67.9 | 2.1 |
| MIP18 | 1249 | 1224 | 720 | 88.4 | 284.9 | 3.2 |
| MIP19 | 1855 | 1886 | 192 | 8.6 | 54.9 | 6.4 |
| MIP20 | 235 | 378 | 168 | 120.6 | 267 | 2.2 |
利用マシン:Pentium1.5GHz +1Gバイトメモリ。 以下実験例は同一マシンによるもの。
3.3. 内点法の安定化
一部の大規模問題に見られる性質:
- 変数や制約式の数値的な大きさにばらつきがある
- 解において大量の制約式が縮退している
が引き起こす数値的問題に対する対策を改良して、計算の安定性を向上しました。この改良はすべての内点法による解法(直線探索法・信頼領域法・高次方向を用いる線形計画問題専用内点法)に有効です。この対策の組み込みにより、10万変数以上の大規模問題を含む線形計画問題115問のセットで全問題が正常に最適化できました(以前は3問失敗)。また1つの問題(14万変数、28万制約)では1176秒だった計算時間が404秒に短縮しています。
3.4. 基底からのリスタート機能
単体法・有効制約法によって線形・二次計画問題を解いた際に、その最適解の情報(基底)を利用し、類似の問題の最適化を高速化します。この求解をリスタートと言います。類似の問題とは、制約の上下限値、目的関数の係数、制約式の係数行列の要素、ヘッセ行列の要素(二次計画の場合)のそれぞれ一部が異なる問題を想定しています。次は線形計画問題の単体法による求解について、通常の単体法による求解時間と、類似の問題(違いは数個の制約式上限)の基底情報を利用した場合の求解時間を比較したものです。
| 問題 | 変数 | 制約式 | 単体法 | リスタート |
|---|---|---|---|---|
| LP1 | 3489 | 2325 | 10.4秒 | 1.1秒 |
| LP2 | 946 | 441 | 2.5秒 | 0.9秒 |
| LP3 | 1988 | 941 | 6.9秒 | 1.2秒 |
| LP4 | 2750 | 398 | 3.3秒 | 0.5秒 |
| LP5 | 2031 | 2158 | 7.0秒 | 1.0秒 |
いずれも基底情報を使うと数倍に高速化され、類似の問題を連続して解く場合にリスタート機能が有効であることがわかります。


