4.2. 数独

次の数独の問題を PySIMPLE で記述してみましょう．

数独とは 3×3 のブロックに区切られた 9×9 の正方形の枠内に次を満たすように 1～9 までの数字を入れるパズルです．

• 空いているマスに 1～9 のいずれかの数字を入れる

• 各値は縦の各列に 1 つずつ入る

• 各値は横の各行に 1 つずつ入る

• 各値は太線で囲まれた 3×3 のブロック内に 1 つずつ入る

• 初期条件を満たす

数独の変数は，各マスについて，各値が「入る」もしくは「入らない」という状態を表現できるものとなります． ここでは，入る場合は 1，入らない場合は 0 を取るような変数 \(x_{値, マス}\) を導入します． 値は 1 から 9 を，マスは左上の (1, 1) から右下の (9,9) をとります．

このとき上記の制約はどのように表すことができるでしょうか．各制約について見ていきましょう．

空いているマスに 1～9 のいずれかの数字を入れる

マス (1,1) を例に考えると，このマスには 1 から 9 のいずれかの値が入ります． 言い換えると，\(x_{1, (1,1)}, \cdots, x_{9, (1,1)}\) のうちちょうど 1 つが 1 となっている， すなわち，これらを足すと必ず 1 になると考えることができます．

\[x_{1, (1,1)} + x_{2, (1,1)} + \cdots + x_{9, (1,1)} = 1\]

これを値 \(v \in Val=\{1, .., 9\}\) と \(\sum\) を用いて表現すると次のようになります．

\[\sum_{v \in Val}x_{v, (1,1)} = 1\]

この制約が各マス (r,c) で成立しているので，1 つ目の制約は \(r \in Row=\{1, .., 9\}\), \(c \in Col=\{1, .., 9\}\) を用いて次のように記述できます．

\[\sum_{v \in Val}x_{v, (r,c)} = 1, \quad \forall r \in Row, c \in Col\]

各値は縦の各列に 1 つずつ入る

値 1 と 1 列目を例に考えてみましょう．値 1 は 1 列目のいずれかに入ります． 1 列目は (1,1), .., (9,1) のマスから成っているので，このうちちょうど 1 つが 1 となります．

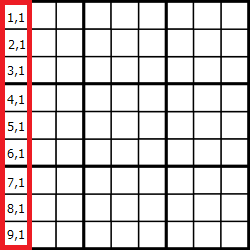
これは次のように表現することができます．

\[x_{1, (1,1)} + x_{1, (2,1)} + \cdots + x_{1, (9,1)} = 1\]

すなわち，

\[\sum_{r \in Row}x_{1, (r,1)} = 1\]

となります． これを任意の値 v と任意の列 c について考えると，次のように記述できます．

\[\sum_{r \in Row}x_{v, (r,c)} = 1, \quad \forall v \in Val, c \in Col\]

各値は横の各行に 1 つずつ入る

列のときと同様に次のように表現することができます．

\[\sum_{c \in Col}x_{v, (r,c)} = 1, \quad \forall v \in Val, r \in Row\]

各値は太線で囲まれた 3×3 のブロック内に 1 つずつ入る

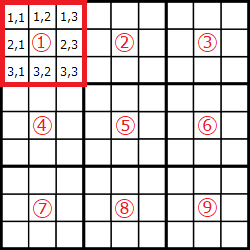
例えば，値 1 が左上のブロック ① に入るという制約は次のように表現することができます．

\[x_{1, (1,1)} + x_{1, (1,2)} + x_{1, (1,3)} + x_{1, (2,1)} + \cdots + x_{1, (3,3)} = 1\]

これは，Block1={(1,1), .., (3,3)} という集合を用意すると，

\[\sum_{(r,c) \in Block1}x_{1,(r,c)} = 1\]

と表現することができます．

他のブロックについても汎用的に記述するにはどうすればよいでしょうか．準備として， Blocks={(①, (1,1)), .., (①, (3,3)), (②, (1,4)), .., (⑨, (9,9))} という集合を用意すると， 先ほどの制約は，

\[\begin{split}\sum_{\begin{smallmatrix}(r,c) \\ (1,r,c) \in Blocks\end{smallmatrix}}x_{1,(r,c)} = 1\end{split}\]

と表現できます． 任意の値 v と任意のブロック \(n \in\) Blocks(0)={①, .., ⑨} について考えると，

\[\begin{split}\sum_{\begin{smallmatrix}(r,c) \\ (n,r,c) \in Blocks\end{smallmatrix}}x_{v,(r,c)} = 1, \quad \forall v \in Val, n \in Blocks(0)\end{split}\]

と記述できます．ここで Blocks(0) は三次元集合 Blocks の一次元目を表します．

初期条件を満たす

初期値集合 Init = {(5,1,1), (6,2,1), .., (9,9,9)} を用意すると，次のように表現することができます．

\[x_{v,(r,c)} = 1, \quad (v,r,c) \in Init\]

以上のことを反映し，汎用化させた結果は以下のようになります．

\[\begin{split}\begin{array}{ll} \bf{集合} \\ \hline Val = \{1, .., 9\} & 値集合 \\ \hline Row = \{1, .., 9\} & 行集合 \\ \hline Col = \{1, .., 9\} & 列集合 \\ \hline Blocks = \{(1,1,1), .., (1,3,3), (2,1,4), .., (9,9,9) \} & ブロック集合 \\ \hline Init = \{(5,1,1), (6,2,1), .., (9,9,9) \} & 初期値集合 \\ \hline \\ \bf{0-1 整数変数} \\ \hline x_{v,r,c} & 値 v がマス (r,c) に入るとき 1，入らないとき 0 をとる変数 \\ \hline \\ \bf{制約} \\ \hline \sum_{v \in Val}x_{v,r,c} = 1, \quad \forall r \in Row, c \in Col & 各マスにはいずれかの値を入れる \\ \hline \sum_{r \in Row}x_{v,r,c} = 1, \quad \forall v \in Val, c \in Col & 各値は縦の各列に 1 つずつ入る \\ \hline \sum_{c \in Col}x_{v,r,c} = 1, \quad \forall v \in Val, r \in Row & 各値は横の各行に 1 つずつ入る \\ \hline \sum_{\begin{smallmatrix}(r,c) \\ (n,r,c) \in Blocks\end{smallmatrix}}x_{v,r,c} = 1, \quad \forall v \in Val, n \in Blocks(0) & 各値は 3 \times 3 のブロック内に 1 つずつ入る \\ \hline x_{v,r,c} = 1, \quad (v,r,c) \in Init & 初期条件を満たす \\ \hline \end{array}\end{split}\]

これを PySIMPLE で記述すると，次のようになります．:

from pysimple import Problem, Set, Element, BinaryVariable, Sum, Parameter

Vals = Rows = Cols = Set(value=range(1, 10))
v = Element(set=Vals)
r = Element(set=Rows)
c = Element(set=Cols)
Blocks = Set(value=[(s+1, s//3*3+t//3+1, s%3*3+t%3+1) for s in range(9) for t in range(9)])
b = Element(set=Blocks)  # b(0) は Block 番号
print(Blocks)

Init = Set(value=[(5, 1, 1), (6, 2, 1), (8, 4, 1), (4, 5, 1), (7, 6, 1), (3, 1, 2), (9, 3, 2), (6, 7, 2), (8, 3, 3), (1, 2, 4), (8, 5, 4), (4, 8, 4), (7, 1, 5), (9, 2, 5), (6, 4, 5), (2, 6, 5), (1, 8, 5), (8, 9, 5), (5, 2, 6), (3, 5, 6), (9, 8, 6), (2, 7, 7), (6, 3, 8), (8, 7, 8), (7, 9, 8), (3, 4, 9), (1, 5, 9), (6, 6, 9), (5, 8, 9), (9, 9, 9)])
init = Element(set=Init)

prob = Problem(name='数独')
x = BinaryVariable(index=(v,r,c))  # 値 v が (r,c) に入るか

prob += Sum(x[v,r,c], v) == 1          # 各マスにはいずれかの値
prob += Sum(x[v,r,c], r) == 1          # 各値は各列のいずれか
prob += Sum(x[v,r,c], c) == 1          # 各値は各行のいずれか
prob += Sum(x[v,b(1,2)], b(1,2)) == 1  # 各値は各ブロックのいずれか
prob += x[init] == 1                   # 初期条件

print(prob)
prob.solve()

print(x[x[v,r,c].val==1])

inittable = Parameter(index=(v,r,c), value=dict.fromkeys(Init, 1))
resulttable = dict(x.val.items())  # dump as dict
showsudoku(Rows, Cols, Vals, inittable)
showsudoku(Rows, Cols, Vals, resulttable)

ここで showsudoku は数独のテーブルを整形して出力するための次のような関数です．:

def showsudoku(Rows, Cols, Vals, table):
    from sys import stdout

    for r, in Rows:
        if r in (1, 4, 7):
            stdout.write("+-------+-------+-------+\n")
        for c, in Cols:
            for v, in Vals:
                if table[v,r,c] == 1:
                    break
            else:
                v = ' '
            if c in (1, 4, 7):
                stdout.write("| ")
            stdout.write(str(v) + " ")
        stdout.write("|\n")
    stdout.write("+-------+-------+-------+\n")

モデルを実行させると，最後に次のような出力が得られ，問題が解けていることが分かります．:

+-------+-------+-------+
| 5 3   |   7   |       |
| 6     | 1 9 5 |       |
|   9 8 |       |   6   |
+-------+-------+-------+
| 8     |   6   |     3 |
| 4     | 8   3 |     1 |
| 7     |   2   |     6 |
+-------+-------+-------+
|   6   |       | 2 8   |
|       | 4 1 9 |     5 |
|       |   8   |   7 9 |
+-------+-------+-------+
+-------+-------+-------+
| 5 3 4 | 6 7 8 | 9 1 2 |
| 6 7 2 | 1 9 5 | 3 4 8 |
| 1 9 8 | 3 4 2 | 5 6 7 |
+-------+-------+-------+
| 8 5 9 | 7 6 1 | 4 2 3 |
| 4 2 6 | 8 5 3 | 7 9 1 |
| 7 1 3 | 9 2 4 | 8 5 6 |
+-------+-------+-------+
| 9 6 1 | 5 3 7 | 2 8 4 |
| 2 8 7 | 4 1 9 | 6 3 5 |
| 3 4 5 | 2 8 6 | 1 7 9 |
+-------+-------+-------+

このモデルを PySIMPLE で記述するためのポイントをいくつか示します．:

Blocks = Set(value=[(s+1, s//3*3+t//3+1, s%3*3+t%3+1) for s in range(9) for t in range(9)])
b = Element(set=Blocks)  # b(0) は Block 番号
prob += Sum(x[v,b(1,2)], b(1,2)) == 1  # 各値は各ブロックのいずれか

ここではまず，三組み Blocks を作成しています． print(Blocks) をすると，上記の要素から成ることが確認できます． b は三組みの任意の 1 つを表す添字です． ブロックの制約 \(\sum_{\begin{smallmatrix}(r,c) \\ (n,r,c) \in Blocks\end{smallmatrix}}x_{v,r,c} = 1\) では三組みの後ろ 2 つについての和をとる必要があります．これは次のように表現することができます．

\[\begin{split}\sum_{\begin{smallmatrix}b(1,2) \\ b \in Blocks\end{smallmatrix}}x_{v,b(1,2)} = 1, \quad \forall v \in Val, b(0) \in Blocks(0)\end{split}\]

ここで b(1,2) は添字 b の 1 番目と 2 番目(0 始まり)を表します．

同様に初期条件も三組を考えて次のように表現します．:

Init = Set(value=[(5, 1, 1), (6, 2, 1), .., (9, 9, 9)])
init = Element(set=Init)
prob += x[init] == 1                   # 初期条件

print(x[x[v,r,c].val==1])

この部分では求解後に値が入った組合せを確認しています． 三組だけを取り出したい場合は (x[v,r,c].val==1).set で OK です．

inittable = Parameter(index=(v,r,c), value=dict.fromkeys(Init, 1))
resulttable = dict(x.val.items())  # dump as dict
showsudoku(Rows, Cols, Vals, inittable)
showsudoku(Rows, Cols, Vals, resulttable)

この部分では数独のテーブルを整形して出力しています． showsudoku はキーが (1,1,1), .., (9,9,9)，値が 0 か 1 である辞書を受け取る関数です．

inittable ではまず，dict.fromkeys(Init, 1) で集合から辞書に変換しています．このままでは定義域が不足しているので， 定義域が (v,r,c) の Parameter に value として渡すことで目的の辞書を作成しています． Parameter は value で渡された部分はその値を，それ以外は値を 0 とする辞書を作成するためです． また，resulttable では求解後の変数の値を辞書に dump しています．

sample.sudoku.showsudoku(Rows, Cols, Vals, table)

sample.sudoku.sudoku(**kwds)

数独