Nuorium Optimizer の派生製品に関しましては以下をご覧ください。
SCHOpt
1. 概要
SCHOpt は、弊社自社開発の運転計画モデリングフレームワークです。
様々な機器が関連しているようなシステムにおいて、運転コストのような指標を最小とする各機器の運転計画を立てることができます。
グラフィカルなインターフェースを持ち、機器や物の流れを表すアイコン(Visio ステンシル)をドラッグ&ドロップするだけで、複雑なネットワークモデルを構築することができます。
さらに、機器オブジェクトを自在にカスタマイズすることができ、様々なモデルを迅速かつ柔軟に構築することができます。
モデル例は以下のようになります。
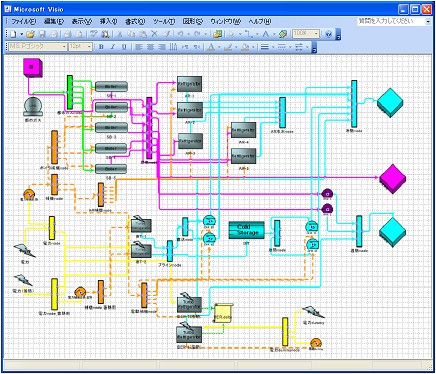
2. 特徴
- SCHOpt フレームワークにより各種モデリングを短期間で実現できます。
- 最適化ソルバーとして弊社 Nuorium Optimizer を使用していますので、厳密解法から近似解法まで Nuorium Optimizer で実装されている様々な解法が使えます。
- Visio を用いてグラフィカルにモデルの構築が可能です。
- 任意の機器間に自由に制約を加えることも可能です。
- 問題毎にカスタマイズを行いますので、柔軟なシステムを構築できます。
- 問題が明確でない場合でも、問題の具体化からシステムの構築までお手伝いします。
3. 操作イメージ
ユーザインタフェースとして、モデル構築に Visio、データ入出力に Excel を使用しています。
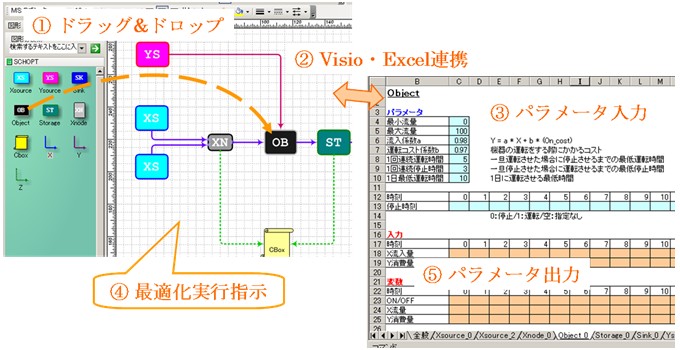
4. 適用例
- プラント運転計画
- 発電計画
- 冷暖房運転計画
- 熱源設備/動力プラント 全体最適化パッケージ/U-OPT ※アズビル株式会社 (クリックするとアズビル株式会社の web ページが開きます。)
5. 動作環境
Microsoft Office Excel、Microsoft Office Visio 及び Nuorium Optimizer が必要になります。 詳細については 資料請求・お問い合わせ よりお問い合わせください。
SNUOPT
SNUOPT リリース終了のご案内
SNUOPT のリリースは終了しています。今後、OS 追従なども含め、メンテナンスの予定はございません。
V24 より R をインターフェースとする RSIMPLE を Nuorium Optimizer に同梱しております。インターフェイスも同様ですので、RSIMPLE のご利用を推奨いたします。


