Ctrl+K

折線関数の線形表現

5. 折線関数の線形表現#

5.1. 説明#

折線関数は区分的に線形であるが，全体としては非線形な関数である． しかし区分的に線形であるために，これらを選択する形で インジケータ変数 を用いると， 折線関数を線形に表現できる．

折線関数 \(f(x)\) が連続で，\(x\) の定義域がその中において \(f(x)\) が線形関数とみなせる \(n\) 個の区間に分割される場合を考える． この時 \(f(x)\) は次のように表される．

(5.2)#\[\begin{split}& y = f(x) = \sum_{i=1}^n S_i\cdot x_i + C, \\ & x = \sum_{i=1}^n x_i, \\ & 0 \leq x_i \leq L_i,~ \forall i\in\{1,\ldots,n\}, \\ & L_i\cdot z_i \leq x_i \leq L_i\cdot z_{i-1},~ \forall i\in\{1,\ldots,n\}\end{split}\]

ここで各定数・変数は次のとおり．

  • \(z_i\) は インジケータ変数

  • \(S_i\) は各折線の傾き

  • \(C\) は \(x=0\) の時の \(y\) の値

  • \(L_i\) は各区間の幅

上記で \(z_0,z_n\) は \(z_0=1\)，\(z_n=0\) と固定しても一般性を失わない． よって必要な インジケータ変数 の実際の総数は \(n-1\) 個である．

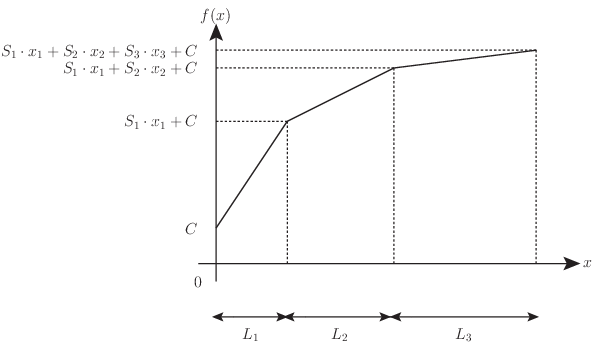
折線関数の例

図 5.1 折線関数の例#

具体的に \(3\) つの区間に分割されている折線関数を定式化してみる (図 5.1 参照)．

(5.3)#\[\begin{split}& y = S_1\cdot x_1 + S_2\cdot x_2 + S_3\cdot x_3 + C, \\ & x = x_1 + x_2 + x_3, \\ & 0 \leq x_1 \leq L_1, \\ & 0 \leq x_2 \leq L_2, \\ & 0 \leq x_3 \leq L_3, \\ & L_1\cdot z_1\leq x_1\leq L_1 ~~ (L_1\cdot z_1\leq x_1\leq L_1\cdot z_0), \\ & L_2\cdot z_2\leq x_2\leq L_2\cdot z_1, \\ & 0\leq x_3\leq L_3\cdot z_2 ~~ (L_3\cdot z_3\leq x_3\leq L_3\cdot z_2)\end{split}\]

本定式化により，インジケータ変数 \(z_1,z_2\) の組み合わせで，各場合を表現できている事になる． 以下，その事を確認してみる．

  • \((z_1,z_2) = (0,0)\) の時

(5.4)#\[\begin{split}& 0 \leq x_1 \leq L_1, \\ & 0 \leq x_2 \leq 0, \\ & 0 \leq x_3 \leq 0\end{split}\]

この時，\((x_2,x_3) = (0,0)\) と固定され，\(x_1\) により \(L_1\) の区間が表現されている．

  • \((z_1,z_2) = (1,0)\) の時

(5.5)#\[\begin{split}& L_1 \leq x_1 \leq L_1, \\ & 0 \leq x_2 \leq L_2, \\ & 0 \leq x_3 \leq 0\end{split}\]

この時，\((x_1,x_3) = (L_1,0)\) と固定され，\(x_2\) により \(L_2\) の区間が表現されている．

  • \((z_1,z_2) = (1,1)\) の時

(5.6)#\[\begin{split}& L_1 \leq x_1 \leq L_1, \\ & L_2 \leq x_2 \leq L_2, \\ & 0 \leq x_3 \leq L_3\end{split}\]

この時，\((x_1,x_2) = (L_1,L_2)\) と固定され，\(x_3\) により \(L_3\) の区間が表現されている．

  • \((z_1,z_2) = (0,1)\) の時

\(L_2\cdot z_2\leq x_2\leq L_2\cdot z_1\) という制約があるため，選ばれることは無い．

5.2. 関連#

目次