Ctrl+K

セパラブル・モデル

7. セパラブル・モデル#

7.1. 説明#

セパラブル・モデルの MIP による近似について説明する． ここにセパラブル・モデルとは，セパラブルな関数 をもつ数理計画モデルの事である．

7.1.1. セパラブル・モデルの MIP による定式化#

セパラブル・モデルを MIP として定式化する為には，セパラブルな関数 の非線形項を線形近似する必要がある． ここでは，例として二次の非線形項がある，凸計画問題のセパラブル・モデルの定式化を以下に示す．

(7.1)#\[\begin{split}& \mathrm{Minimize:}~ x_1^2 - 4x_1 -2x_2, \\ & \mathrm{subject~to:}~ \\ & x_1 + x_2 \leq 4, \\ & 2x_1 + x_2 \leq 5, \\ & -x_1 + 4x_2 \geq 2, \\ & x_1,x_2 \geq 0\end{split}\]

上の例で非線形項 \(x_1^2\) を取り除くことを考える． ここでは区間 \(0\leq x_1\leq 2.5\) を \(0 \leq x_1 \leq 1\)， \(1\leq x_1 \leq 2\)， \(2\leq x_1 \leq 2.5\) の三つの区間に分割し，図 7.1 のように折線で近似する．

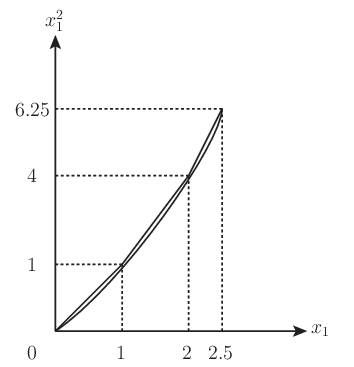
折線による近似の例

図 7.1 折線による近似の例#

定式化は次のとおり．

(7.2)#\[\begin{split}& x_1 = 0\lambda_1 + 1\lambda_2 + 2\lambda_3 + 2.5\lambda_4, \\ & y = 0\lambda_1 + 1\lambda_2 + 4\lambda_3 + 6.25\lambda_4, \\ & \lambda_1 + \lambda_2 + \lambda_3 + \lambda_4 = 1, \\ & \lambda_i \geq 0,~ \forall i\in\{1,\ldots,4\}\end{split}\]

これら制約条件に加えて「\(\lambda_i\) は高々二つの隣り合った \(\lambda_i\) のみがゼロではない．」という制約を課す． この制約は \(y\)，\(x_1\) が折線上の値を取る事を保証するものである． この制約を定式化するには インジケータ変数 \(\delta_i(i=1,\ldots,3)\) を導入して， 次のように定式化すればよい．

(7.3)#\[\begin{split}& \lambda_1 - \delta_1 \leq 0, \\ & \lambda_2 - \delta_1 - \delta_2 \leq 0, \\ & \lambda_3 - \delta_2 - \delta_3 \leq 0, \\ & \lambda_4 - \delta_3 \leq 0, \\ & \delta_1 + \delta_2 + \delta_3 = 1\end{split}\]

この条件全体を \(A(\lambda,\delta)=0\) と書くことにする．

上記を踏まえ，上の例のセパラブル・モデルを MIP として定式化すると，次のようになる．

(7.4)#\[\begin{split}& \mathrm{Minimize:}~ y - 4x_1 - 2x_2, \\ & \mathrm{subject~to:}~ x_1 + 2x_2 \leq 4, \\ & 2x_1 + x_2 \leq 5, \\ & -x_1 + 4x_2 \geq 2, \\ & -x_1 + \lambda_2 + 2 \lambda_3 + 2.5 \lambda_4 = 0, \\ & -y + \lambda_2 + 4 \lambda_3 + 6.25 \lambda_4 = 0, \\ & \lambda_1 + \lambda_2 + \lambda_3 + \lambda_4 = 1, \\ & y, x_1, x_2, \lambda_1, \lambda_2, \lambda_3, \lambda_4 \geq 0, \\ & A(\lambda,\delta)=0\end{split}\]

以上よりセパラブル・モデルは LP として表現できるとわかった． なお今回の問題は次の特徴を持つため，上記定式化から条件 \(A(\lambda,\delta)=0\) をとり除く事ができる．

  • \(y\) は最小化される目的関数に含まれている

  • \(y\) は凸関数である

注釈

以上に述べた定式化には折線近似を用いているので，ある程度の不正確さは伴う． しかし不正確性は近似する直線の数を増やすことによって減らす事ができる． また不正確性を取り除く事が非常に重要であると考えられる場合には， 本定式化で得られた最適解付近の分割を細かくし，再度最適化を行うという方法もある．

7.1.2. 凸関数の線形近似の一般化#

それは非線形項 \(y = f(x)\) を区間 \(i\) に分割する時，新しい変数 \(\lambda_i\) を導入し， 次のように定式化する．

(7.5)#\[\begin{split}& y = \lambda_i\cdot f(x_i), \\ & x = \sum_{i\in I} \lambda_i\cdot x_i, \\ & \sum_{i\in I} \lambda_i = 1\end{split}\]

これは前項で示した凸関数の線形近似を一般化である．

7.2. 関連#

参考文献

[1]

H.P.ウイリアムス. 数理計画モデルの作成法. 産業図書, 1995.

目次