3. 定式化の強弱#
3.1. 説明#
3.1.1. 自明に余分な制約条件#
次の制約条件があったとする.
ここで \(b_t\) は \(0\)-\(1\) 整数変数であり, \(F_t\) は \(0\) または \(1\) をとる定数とする.
この制約は \(F_t=0\) なる \(t\) に対しては \(b_t\) は \(0\) または \(1\) がとれる自由な変数であり, \(F_t=1\) なる \(t\) に対しては \(b_t=0\) と拘束する変数であることを指定する制約条件である.
今考えているこの制約条件は例えば,\(b_t\) が \(t\) 日目に出勤する (\(1\)) かしない (\(0\)) かどうかを表し, \(F_t\) が \(t\) 日目に出勤を禁止する (\(1\)) かしない (\(0\)) かどうかを表すような場合を記述するものである.
3.1.1.1. 記述の効率性#
さてこの制約式は当然ながら集合 \(T\) の要素数 \(|T|\) だけある. しかし \(F_t=0\) の場合は何も制約条件を課していない. つまり余分に制約条件を考えていることになり, もし計算機が数式を解釈しようとすれば,無駄な数式が混じっており,効率が悪い.
また現実の問題でそもそも \(F_t=1\) はイレギュラーな状況を想定してのことで, これを満たす \(t\) はとても少ないことが予想されるならば, この余分さがとても多くなることは珍しいことではなくなってしまう.
以上から単純な記述でありながら,害のある記述とわかる. 無駄のない記述をするためには,\(F_t=1\) のみ記述ができればよい. よって次のような記述がよいとわかる(ラフな記述).
これは「\(F_t=1\) であるような \(t\) について,\(b_t=0\) でありなさい」という制約条件である. カンマ以降で \(t\) の範囲を制限しているが,このことをもっと明示的に述べれば, \(T\) の元のうち,\(F_t=1\) を満たす \(t\) の集合 \(T_F\) を考え, その集合の元で制約条件を記述すればよい.
つまり上記のように集合を定義して,次の制約条件を考えればよい.
3.1.1.2. まとめ#
以上のことを定式化テクニックとしてまとめると次のとおり.
制約条件式の記述のうち, 全く何も課さない制約条件が記述されることがある. このような制約条件をここでは「自明に余分な制約条件」とよぶことにする.
自明に余分な制約条件を認めるおかげで, 定式化に表れる制約条件を単純に記述できるが, その代償として無駄な情報を計算機に与えてしまう.
これを回避するためには全称記号 \(\forall\) が作用する集合を適宜狭める必要がある. つまり新たに部分集合を定義して, その集合の元で添字付けた制約条件を記述する必要がある.
注意
定式化が主眼でないような数理最適化のテキストでは,標準形 で済ませてしまうか, 自明に余分な制約条件で個々の問題の定式化を簡便に図ることが度々ある. このため実際の定式化を行うにあたって, 無駄な制約条件を大量に記述していることに気付かないということが少なくない.
自明に余分な制約条件を取り除くことは良い定式化に欠かせない基本的なテクニックである.
3.1.2. 非自明に余分な制約条件#
自明に余分な制約条件以外の余分な制約条件は非自明な余分さを持っている. このことを以下に述べる.
3.1.2.1. 強い定式化と弱い定式化#
まず「強い定式化」「弱い定式化」を定義する.
与えられた問題に対して二つの定式化 \(\mathcal{M}_1,\mathcal{M}_2\) ができたとする. そしてこれら定式化の 実行可能領域 および線形な 緩和問題 とした 実行可能領域 をそれぞれ \(\mathcal{Z}_1,\mathcal{Z}_2\) および \(\mathcal{R}_1,\mathcal{R}_2\) とする.
このとき \(\mathcal{Z}_1=\mathcal{Z}_2\) 且つ \(\mathcal{R}_1\subset \mathcal{R}_2\) ならば, 定式化 \(\mathcal{M}_1\) は定式化 \(\mathcal{M}_2\) より強い定式化であるという. また同時に,定式化 \(\mathcal{M}_2\) は定式化 \(\mathcal{M}_1\) より弱い定式化であるという.
つまり 実行可能領域 が狭いほど,より厳しいことを定式化できているため, その分だけ 上界値 ・ 下界値 に制限を狭めることになり, 従って定式化に強度を定めえるということである.
3.1.2.2. 定式化の強さと線形緩和問題#
線形な 緩和問題 を議論する際に定式化の強さを論じることがある. それは次のようなものである.
まず 図 3.1 を見よう. 黒点で示しているのが 実行可能解 である.
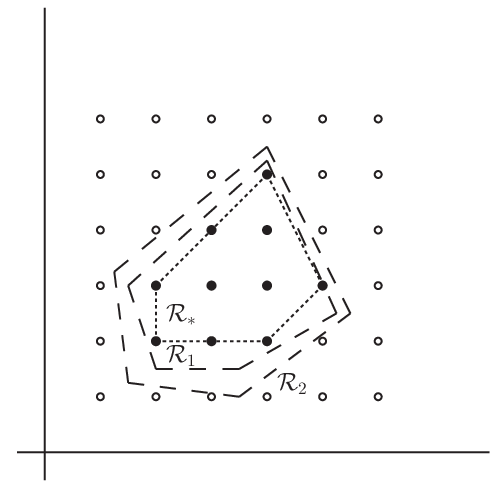
図 3.1 実行可能領域と定式化の強さ#
そして \(\mathcal{R}_1\) と \(\mathcal{R}_2\) がそれぞれ定式化 \(\mathcal{M}_1\) と \(\mathcal{M}_2\) に対する 実行可能領域 を表す. \(\mathcal{R}_1\subset\mathcal{R}_2\) なので \(\mathcal{M}_1\) は \(\mathcal{M}_2\) よりも強い定式化である. 理想的には 実行可能解 の凸包 \(\mathcal{R}_*\) (与えられた集合を含む最小の 凸集合) に等しい定式化 \(\mathcal{M}_*\) が最も強い定式化となる.
図 3.1 は \(2\) 変数に限った場合なので, \(2\) 次元平面で 実行可能領域 について強い弱いなどと,手計算や絵に描いて確かめることができる. しかし現実の問題を相手にする場合には高次元での議論となるので,そういったことが大変難しいものになる.
そこで強い定式化を得るには,とにかく自明に余分でない制約条件を追加するか, 次のような典型的な例が考えている定式化に表れているかどうかで判断していく.
\(0\)-\(1\) 整数変数 \(x_{i,j},y_j\) があったとする. そして与えられた問題に対する定式化 \(\mathcal{M}_1\) と \(\mathcal{M}_2\) の中に次の制約条件があったとし, 違いはこの二つのみだったとする.
\(\mathcal{M}_2\) の定式化は \(i\) で和をとっているので, 個別に制約を課している \(\mathcal{M}_1\) よりも弱い定式化である. つまり総和をとっているかどうかで,強弱を容易に判断できる. 線形な定式化を行う限りは,このような総和が頻出するので, 今のように定式化の強弱の判断が容易にできる場合が珍しくない.
3.1.2.3. まとめ#
以上をまとめると次のとおり.
一般に定式化の強弱は高次元になるほど難しい.しかし,総和をとっていないかどうかで容易に強弱を判断できる場合が典型的にある.
強い定式化ほど制約条件の数が多くなりやすく,緩和問題 に対する求解時間が増大する傾向にある. このことから 分枝限定法 に対する求解時間に比べて,この増大時間が少ない影響であれば,強い定式化を行うことが望ましい傾向がある. つまり 緩和問題 の解の値と 実行可能解 の初期解との差が大きいほど,強い定式化が望ましい傾向がある.
いつでも強い定式化の方が優れているとは断言できない.試行錯誤が必要になる.
制約条件式はいろいろと加えたほうが良い 切除平面 を得る機会が増す.
Tip
切除平面 について理解を深めるゲーミフィケーションに The Cutting Plane Game がある (図 3.3 参照). これは『組合せ最適化ゲーム「The Cutting Plane Game」のご紹介』でも解説しているように, 無限の選択肢の中からソルバーがどんな 気持ち でカットを入れているのか, 制約条件を書き下すときに思いを馳せることができるようになるかもしれない.
図 3.3 The Cutting Plane Game#
