アルゴリズムとは日本語では処理手順のことを言います。 汎用数理計画法パッケージ Nuorium Optimizer が色々な問題を解くことができるのは様々なアルゴリズムがプログラムされているからです。 ここでは数理計画法・最適化の仕組みを理解する上で必要な情報を分かりやすくご説明致します。 あくまで入門的な位置づけですので数学的に厳密な説明を行う訳ではございませんのでご了承ください。
数理計画法で代表的なアルゴリズムについての簡単な解説
アルゴリズムの説明
アルゴリズムの説明を具体例を見ながら行いたいと思います。
例題
8 枚の金貨を袋に入れた金貨セットを 1000 袋販売します。 袋に 8 枚の金貨を入れる作業をある業者に依頼したのですが、 その業者は 1 袋あたり 1 枚の偽造金貨を混入させました。 業者を逮捕し、横領した合計 1000 枚の本物の金貨を押収したのですが、 それぞれの袋の偽金貨を取り出し本物を 1 枚入れるという作業をする羽目になりました。 偽造金貨は本物の金貨よりも微妙に軽いことが調べから分かっています。 道具は天秤 1 つです。8 枚の金貨から偽金貨を特定する方法を考えてください。

アルゴリズムの作成例
この問題の場合にアルゴリズムは "必ず誰がやっても成功するマニュアル" のようなものであると言えます。
<アルゴリズム>
- 金貨を 4 枚ずつに分けて天秤で比較する
- 軽い方の 4 枚を 2 枚ずつに分けて天秤で比較する
- さらに軽いほうの 2 枚を 1 枚ずつに分けて天秤で比較する
- 最後に軽いほうが偽物の金貨!
アルゴリズムの工夫
上で作成したマニュアル(アルゴリズム)に沿って金貨の詰め替え作業を行っているが、締め切りが迫ってきてしまいました。 作業員を追加で投入しても、結局天秤が一つしかないので作業ははかどりません。そこでマニュアル(アルゴリズム)を見直すことにしました。
<新アルゴリズム1>
- 金貨を 3 枚ずつ天秤で比較する
- 天秤が釣り合えば <CASE A> へ、釣り合わなければ <CASE B> へ
・CASE A
天秤に乗せなかった 2 枚のうち 1 枚が偽物であるのでもう一度天秤にかけて終了
・CASE B
軽かった 3 枚から 1 枚ずつを天秤にかける。釣り合った場合は残りが偽物、釣り合わなければ軽い方が偽物
なんとこの新アルゴリズムでは一袋あたりの天秤の利用回数を 1 回減らすことが出来、 2 回使うのみで判別できるようになります。 これで全体の処理スピードが 1.5 倍に上がり、締め切りまでになんとかなりそうです。 ここで以下の新たなアルゴリズムを提案する者が現れました。
<新アルゴリズム2>
- 金貨を 1 枚ずつ天秤で比較する
- 天秤が釣り合わなければ即終了、釣り合った場合は両方本物
- 釣り合わなかった場合は残りの金貨から 1 枚ずつ天秤で比較する
- 天秤が釣り合わなければ終了、釣り合った場合は両方本物
- 。。。
このアルゴリズムを提案した者はこのように主張しました。
「運が良ければ 1 度の試行で終了だから新アルゴリズム1より性能がよいのではないか!?」
この者の主張はそういう場合もあるし、そうでない場合もあるということになります。 アルゴリズムとして安定していないわけですので、ひとつの賭けです。 アルゴリズムを構築するときには "ある条件(この場合勘が冴えている)のときにだけ速い" というのは好ましくありません。 平均的な速度 や 最悪のケースの速度 を見積りながらアルゴリズムは構築するものです。

おまけ
問題の条件を少し変えて考えてみましょう。これまでは天秤は一台しかありませんでしたので、 その一台をどのように効率的に利用できるかという点がアルゴリズムの評価そのものでした。 では、天秤が無限(コインが 8000 枚なので 4000 台あれば十分)で作業する人間も十分にいたとします。 この場合の一番最速なアルゴリズムはどうなるでしょう。 4000 人の作業員が、それぞれコインを 2 枚ずつ手に取り、皆で一斉に天秤で重さを比較すればそれで終了です。 当然 4000 人が一気に作業するスペースが必要ですので、込み合って時間がかかる可能性もありますし、 そもそも 4000 台の天秤を並べるだけでも大変そうです。 これは実際のプログラムのアルゴリズムに例えると、利用してよいメモリ領域の大きさや、 同時に利用できるプロセス数にあたります。そういった条件によってもアルゴリズムの評価は変わっていくものなのです。

線形計画法
ここでは数理計画法の中の線形計画法についてご紹介します。 線形計画法とは線形計画問題を解く解法・アルゴリズムを総称したものです。
線形計画問題とは
決定変数が連続変数で、制約条件や目的関数が全て線形の式で表現された数理計画問題を線形計画問題と呼びます。 線形の式とは、変数の 1 次式で記述してある式を指します。
例えば下のグラフのようなイメージになります。 下のグラフは 2 変数( x ,y )で制約式が 3 つの最適化問題をグラフ化したものになります。 3 つの制約式を満たす範囲は水色部分(実行可能領域)になり、そのどこかが最適解ということになります。 線形計画問題は実行可能領域が凸多面体になり、最適解はその頂点のいずれかになることが知られています。 下の例では目的関数に触れていませんが、目的関数がどんな形状であっても(線形である必要はありますが)赤い○で囲った頂点のいずれかになります。
アルゴリズムイメージ
単体法
単体法はイメージとしては凸多面体である実行可能領域の頂点を探索するアルゴリズムになります。 単体法は数理計画法の歴史の中で最も古いアルゴリズムで、数理計画法の誕生と共に産声を上げました。 単体法についてはメールマガジンのバックナンバー「数理計画法の誕生と発展」をご覧ください。
内点法
内点法は凸多面体である実行可能領域の内部を探索するアルゴリズムになります。 直感的には表面を探索するよりは近道が出来そうですので、単体法に比べて高速なアルゴリズムのように感じられるかも知れませんが、 実際のところは問題によってそうとは言い切れません。 詳しくはメールマガジンのバックナンバー「新・線形計画法 内点法 VS 単体法」をご覧ください。
線形計画法で取り扱うことのできる応用問題
- 輸送・配送問題
- 配合問題(肥料や化学製品、軽重金属)
- 最大流問題
- ダイエット問題
- ナップサック問題
- 大規模な離散問題の連続緩和問題
Nuorium Optimizer におけるアルゴリズムの工夫
単体法
単体法アルゴリズムの理論は既に成熟しておりますが、プログラムとして実装するに当たり性能を左右する工夫が数多くある事は、実はあまり知られていません。
代表的なものを幾つか紹介しましょう。
例えば一般の数理計画法の教科書では、最初の実行可能基底解を得るためにビッグ M 法がよく紹介されますが、 この方法では高速・安定に実行可能基底解を得る事はできません。 また、実行可能基底解から別の実行可能基底解に移動する際には、相対コスト係数を見る流儀・実際の減少量を見る流儀など複数のアイデアが存在し、 これらをうまく調整する必要があります。さらに、内部の行列データの保持方法を工夫する事により、計算量を格段に圧縮する事ができます。
この他にも様々な工夫がありますが、これら一つ一つを丁寧に組み込む事で、 Nuorium Optimizer の単体法は高い性能を誇っています。
内点法
線形計画問題に対する内点法は、大きく分けて「主内点法」「主双対内点法」の二種類が存在します。 前者の方が歴史がありますが、実用上優れているのは後者の「主双対内点法」だとの見方が一般的です。 「主双対内点法」の中にも様々な流派がありますが Nuorium Optimizer で採用しているアルゴリズムの大枠は「予測子・修正子法」と呼ばれる方法です。
ただし Nuorium Optimizer では単に「予測子・修正子法」をそのまま適用している訳ではありません。 主双対内点法の理論において、収束性を保証する生命線とも言える、バリアパラメータの更新ルールは独自の方法を採用しています。 理論上優れた更新ルールは、求解速度の観点からは必ずしもベストな選択肢ではありません。
また、内点法において最も計算時間を要する、疎対称連立一次方程式の計算ロジックに関しては多数の独自工夫が凝らされています。 例えば Bunch-Parlett 分解と呼ばれる方法を適用する事により、内部で自由変数を分解する事無く、そのまま取り扱う事ができます。
さらに、問題のスケーリング変換や、初期値の設定も高速性・安定性に大きく影響します。 スケール差が大きな問題や、境界領域近くの初期値設定がまずい事は良く知られていますが、 それ以外の性質に関しては殆ど公には知られていないと言って良いでしょう。 これらの問題についても、 Nuorium Optimizer の内点法には現実の問題に対して培ったノウハウが凝縮されています。
混合整数線形計画法
ここでは数理計画法の中の混合整数線形計画法についてご紹介します。 混合整数線形計画法とは混合整数線形計画問題を解く解法・アルゴリズムを総称したものです。
混合整数線形計画問題とは
決定変数の一部が整数変数でなければならないという制約を持つ、線形計画問題を混合整数線形計画問題と呼びます。
線形計画問題 の例に対して変数 x が整数変数だとすると、 実行可能領域(制約条件を満たす領域)は下の図のイメージになります。 x は連続的に全ての値を取れるわけではないので、 下の図の濃い青の部分(厳密には横幅はありませんが)になっています。
小さな例でこのように見ると、実行可能領域自体は小さくなりそうなので探索が楽なように感じるかもしれませんが、 問題は非常に難しくなります。
アルゴリズムイメージ
線形計画問題に対して難しくなる理由は 2 つです。 一つは凸多面体の頂点を探せばよいわけではなくなるので、単体法のようなアプローチができなくなることです。 もう一つは離散変数が現れるので、内点法のように「解に近い方向」を微分によって求めるということもできなくなることです。
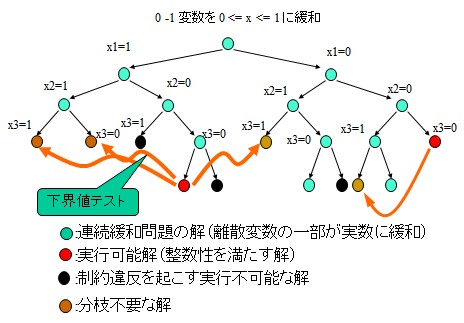
そんなわけでアルゴリズムの発想の出発点としては非常に素朴な方法である、全探索から出発せざるを得ません。 上記の問題であれば、x が 0, 1, 2, 3, 4, 5 のときの最適解(x を固定して連続変数 y のみに関して解いた結果)を全て求めて比較するというものです。
容易に想像できることですが、この方法だと、結局離散変数の全通り探索が必要になるので大規模問題を現実的な速度で解くことができません。 そこで下のイメージ図のように、全通り探索しなくてよいように、探索の途中で得られる情報を使いながらツリー構造の途中のノード以下を計算の対象から除外(限定)する手法、分枝限定法が主流になっています。
混合整数線形計画法で取り扱うことのできる応用問題
- 施設配置問題+輸送・配送問題
- 発電設備運転計画問題
- ネットワーク設計問題
Nuorium Optimizer におけるアルゴリズムの工夫
分枝限定法において計算するノードを限定する際、具体的には二つの情報を使っています。 一つは得られている実行可能解の情報、もう一つは連続緩和問題の解の情報です。
実行可能解とは、最適解かどうかは分からないが、とりあえず制約条件は(整数性の条件も!)満たしている解のことです。 連続緩和問題の解は整数性の条件を外した問題の解で、目的関数値は必ず元の問題より良くて当り前です。 ある探索ノードで連続緩和問題の解が実行可能解に負けてしまっていれば、 そのノードから派生するノードを調べても最適解は得られないことが明らかなので、探索の範囲から外してもよい。 これが限定操作です。
分枝限定法の高速化の鍵の一つは、良い実行可能解をできるだけ早く見つけることにあります。 しかしながら、連続緩和問題の解は単体法を使えば必ず得られる一方で、 良い実行可能解を得る方法には定まったやり方がありません。 Nuorium Optimizer は、丸め・局所探索などのヒューリスティクスを独自の方法で行い、 良い実行可能解を速く求める工夫を行っています。
この実行可能解探索に特化した方法が 整数計画法 で解説しているメタヒューリスティクスアルゴリズムです。
連続緩和問題の作り方にも工夫の余地があって、ただ整数性の条件を外すだけでは緩和問題の解が元の問題の性質を失って、 全く限定操作の役に立たない場合があります。
Nuorium Optimizer は、与えられた問題から「妥当不等式」という人工的な制約条件を推定し、 これを加えることによって緩和問題の解を改善しています。 この妥当不等式は、Gomory カットなどが知られていますが、教科書通りに実装しても往々にして高速化は望めません。 例えば、Gomory カットは理論的には常に緩和問題の解を良くすることが知られていますが、 数値的性質が悪く単純に加えると元の問題を解きづらい形にしてしまいます。 Nuorium Optimizer は実務的な問題で効果がでるよう、こうした妥当不等式に工夫を施しております。
高速化のもう一つの鍵は分枝限定法にかける前の定式化の前処理です。 整数変数の値の設定の組みあわせを実地にチェックしてみると、論理的帰結によりすべての値の組みあわせが許されるわけではなく、 特定の組みあわせしか許されないことがわかります。 この操作を probing と呼び、ここから新たな制約を推論して、変数の固定や、「妥当不等式」の作成といったことが可能です。 極端なケースでは、probing だけで解が一意に決定してしまう場合も存在します。 Nuorium Optimizer ではこの probing を始めとする前処理の工夫を行って、分枝限定法の負担を軽減しています。
整数計画法
ここでは数理計画法の中の整数計画法についてご紹介します。 整数計画法とは整数計画問題を解く解法・アルゴリズムを総称したものです。
整数計画問題とは
一般に整数計画問題といった場合に、連続変数を含むこともありますがここでは全て離散変数であるような問題のこととして取り扱います。 連続変数を含む問題は 混合整数線形計画問題 を参照ください。
線形計画問題 のところで上げた例題に対して、x と y が共に整数変数という制限を加えたものが、 整数計画問題になります。右のイメージ図で濃い青色の格子点が実行可能な解候補になり、 この中のどれかが最適解ということになります。
アルゴリズムイメージ
混合整数線形計画問題 で紹介した分枝限定法もこの問題に適応することは可能です。 ここでは、全て離散変数の問題に適応できるメタヒューリスティクスアルゴリズム WCSP についてご紹介します。
アルゴリズムはシンプルで、上の図のようにまず初期点から出発しその周辺(近傍)の中で一番よい解を次の解に選択します(改善解)。 これを徹底的に繰り返すことによって、解を更新していくという手法です。 この方法は近似解法と呼ばれており、最適性の保証が無いながら大規模な問題に対して、非常に有効なアルゴリズムです。
整数計画法で取り扱うことのできる応用問題
- 勤務表作成・シフトスケジューリング
- 生産計画・プロジェクトスケジューリング
- 広告配信計画・レコメンデーション
- 施設配置問題
Nuorium Optimizer におけるアルゴリズムの工夫
メタヒューリスティクスアルゴリズムの長所として、大規模問題に対し高速に解が得られることがあげられます。 一方、必ずしも大域的最適性を保証できない、という短所があります。
そのため、Nuorium Optimizer に搭載されている WCSP アルゴリズムは汎用性を考慮して タブーサーチ を採用し、 その短所を補っています。 また、制約に対する重みを動的に変更し、探索方向を効率良くする工夫や、局所解から出られない場合に近傍を動的に拡大する等、 多くの実装上の工夫が組み込まれています。
Nuorium Optimizer が搭載している WCSP アルゴリズムは「京都大学・問題解決エンジンプロジェクト」により生み出されたものです。 Nuorium Optimizer には独自の差分評価テクニックが導入され、さらなる高速化を実現しています。
当然この WCSP アルゴリズムも Nuorium Optimizer に付属の モデリング言語 C++SIMPLE を用いて利用することができ、 一つのモデルファイルで分枝限定法と切り替えて利用することも可能です。 また、様々な組み込み関数(Selection/min/max…)を用意しておりモデリングの自由度とパフォーマンスの向上を実現しています。
その他にも求解設定(初期解生成の乱数やイテレーションを制限)に関する wcsp 特有のオプションが備わっています。 オプションの指定によりシフトスケジューリングなど複数のシフト提案が必要な場合にも対応することができます。
凸二次計画法
ここでは数理計画法の中の凸二次計画法についてご紹介します。 凸二次計画法とは凸二次計画問題を解く解法・アルゴリズムを総称したものです。
凸二次計画問題とは
目的関数が凸な二次式で制約条件が線形で表現できる問題を凸二次計画問題と呼びます。 目的関数が凸の場合にはさらに有効なアルゴリズムを適用することが可能なります。 ここではそういった問題を前提として説明を致します。右のイメージ図は 2 変数の二次で凸な関数の例です。
アルゴリズムイメージ
数理計画法を解く上で最も扱いに注意を要するのは不等式。いくつかの不等式は、 等式として満たされていて、最適解を形成するのに貢献していますが、 いくつかの不等式は最適解の存在する領域を定義しているだけの働きしかしていません。 もちろん、どの不等式が最適解を形成するのに直接貢献しているか (「アクティブ」になっているか)は問題を見ただけではわかりません。 あれかこれかと推定しながら計算を進めます。特に線形計画・凸二次計画の場合には、 このアクティブな不等式群の決定が最適解の探索とほぼ同じであることが知られており、 Nuorium Optimizer に組み込まれている単体法・有効制約法はこの性質を活用した手法です。
凸二次計画法で取り扱うことのできる応用問題
- ポートフォリオ最適化
- 電力潮流計算
Nuorium Optimizer におけるアルゴリズムの工夫
アクティブになった不等式は以降の計算では等式として扱います。例えば x >= 0 という式がアクティブになったら x を 0 に固定してよく、 変数を実質減らして効率良く計算を行うことができます。 例えばポートフォリオ最適化問題などは、x >= 0 という不等式が数多くアクティブになる (0 に固定される変数が多い)ので、 有効制約法に向いた問題であることが知られています。
また、有効制約法はその性質上、アクティブになる不等式制約がおおまかにでも見積もれていれば高速に解を求めることができます。 そのため、似通った CQP を繰り返し解く場合には、アクティブになる不等式制約の情報を引き継ぐことで高速化が図れます。 Nuorium Optimizer の有効制約法には、この機能が実装されており、連続して CQP を解く局面や逐次二次計画法において活用されています。
非線形計画法
ここでは数理計画法の中の非線形計画法についてご紹介します。 非線形計画法とは非線形計画問題を解く解法・アルゴリズムを総称したものです。
非線形計画問題とは
線形計画問題では制約式や目的関数が全て線形の式( 1 次式 )で表すことができる問題とご説明しました。 非線形計画問題は制約式や目的関数が線形でない任意の連続関数として表現される問題ということになります。 例えば sin や cos を用いたり、変数の 2 乗 3 乗、変数同士の積がそれにあたります。 また、離散変数を含む非線形計画問題のアルゴリズムも研究されておりますが、 ここでは離散変数を考慮しない連続変数のみで構成されている問題を考えます。 下の図が 2 変数の問題のイメージです。最大化問題ですと、赤い○が最適解の候補になります。
アルゴリズムイメージ
我々が実は丸い地球を、普段平らだと思って暮しているように、どんなに折れ曲がった曲面でも大抵のものは近寄ってみると、平面に見えます。 非線形最適化とは遠目で見ると曲面上のどこかの点を探しているのですが、 思いきってある点のまわりをぐっとクローズアップすると(線形近似すると)平面に見えてきます。 平面としての「見たて」に従えば例えば線形計画法の方法を使って、解の存在する方角を導くことができます。 もちろん平面としての見立ては完全ではないので、導いた方角はちょっとずれてきますが、大丈夫。 ずれが深刻にならない程度まで進んで、またクローズアップを繰り返せばよいのです。 そうしていつかクローズアップした領域の中に解が含まれるところまで来ればこちらのもの。 解のまわりを今度は顕微鏡的に拡大することを繰り返せば、平面としての「見立て」の精度はどんどん正確になり、 好きなだけ精度良く真の解を求めることができるのです。
非線形計画法で取り扱うことのできる応用問題
- 非線形モデルパラメータのデータへの合わせ込み
- イールドカーブフィッティング
- ロジスティック回帰による判別分析
- 化学プラントの収率最適化
- 蒸気表タービン効率運転モデル
Nuorium Optimizer におけるアルゴリズムの工夫
クローズアップを繰り返して解にのそばに迫る局面では、できるだけ少ないクローズアップでおおまかに解のありそうな場所を特定することが必要。 そのために「メリット関数」という、解への肉迫度合を計測する関数を定義して得られる大局的な情報を活用しています。 Nuorium Optimizer に利用されているアルゴリズムはどこから出発しても必ずいずれかの局所解に辿りつくことができるという理論的な保証(大域的収束性)を備えたものです。
また、クローズアップした領域に解が入ってからの局面では Nuorium Optimizer では解を素早く収束させるために複数のパラメータを同時かつ動的に調整します。 この調整方法も理論的な保証(超一次収束性)があります。 探索方向を導く部分は 線形計画法 の内点法と同一ですので、線形計画法の実装で培った数値的工夫の積み上げによって高速性と安定性が実現されています。


