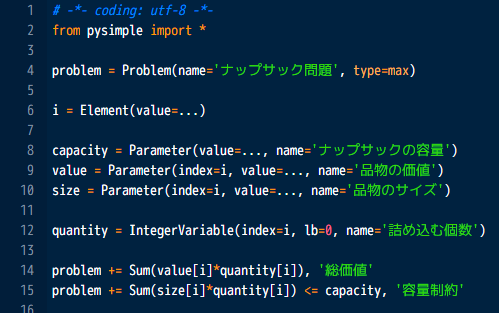
Nuorium Optimizer は「数式ベースの自然で簡潔な記述ができるモデリング言語」「様々な実用的な求解アルゴリズム」「高機能なテキストエディタを備えた GUI 開発環境」を完備し、約 30 年にわたって洗練させ、また発展させている汎用数理最適化パッケージです。

お知らせ
概要
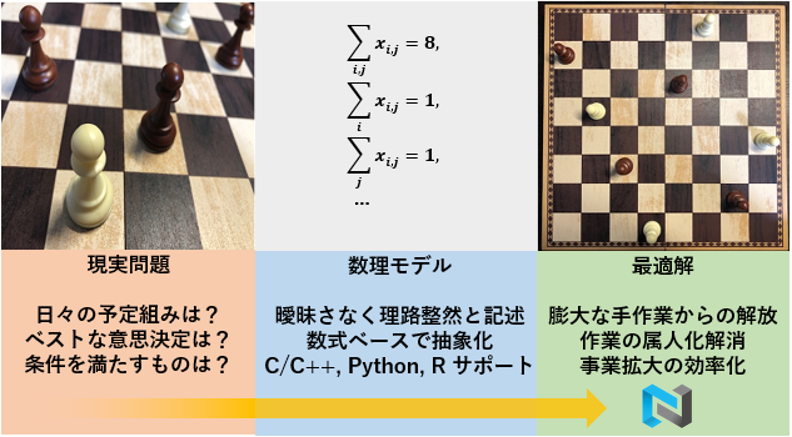
数理最適化とは
汎用数理最適化パッケージ「Nuorium Optimizer」は、“データ”と“やり方(ルール)”がわかっていながら、 解決策が導き出せない現実の問題に対し、最適解を提供するツールです。 最適化ソリューションは様々な分野で広く利用されています。 数理計画法と呼ばれる様々な解法(アルゴリズム)を駆使して現実の問題を解決するというアプローチです。
主な特徴
モデリング言語
求解アルゴリズム
様々な大規模問題を安定かつ高速に求解することを目的に開発しています。最新の実装技術と豊富な求解アルゴリズムにより、Nuorium Optimizer 一つで様々な問題を扱うことができます。
詳しく知りたいかたは 数理最適化アルゴリズム入門 へ
開発環境
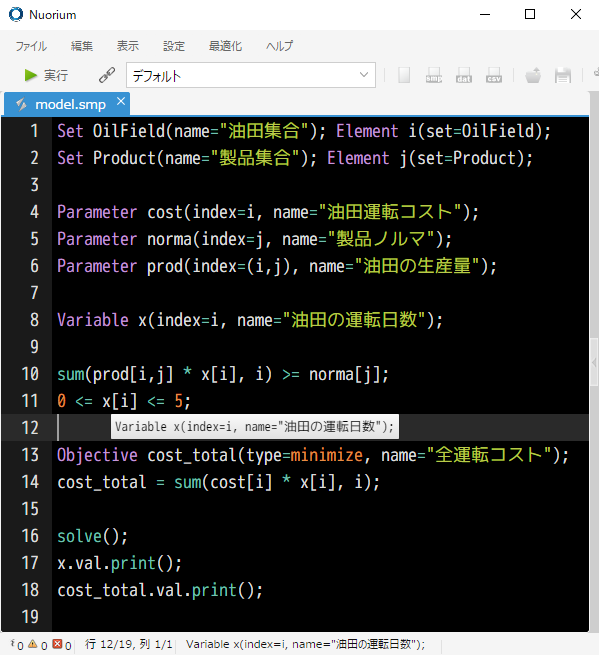
GUI 開発環境 Nuorium がモデル開発を強力に支援します。キーワード自動補完機能やタグジャンプ機能、ファイラや Emacs キーバインドなど、初心者から上級者までが必要とする機能を備えた GUI 開発環境です。

Excel アドインを用いると Excel データと最適化モデルとのやり取りが簡単なマウス操作で可能です。データを Excel で管理することの多い実務家をサポートします。
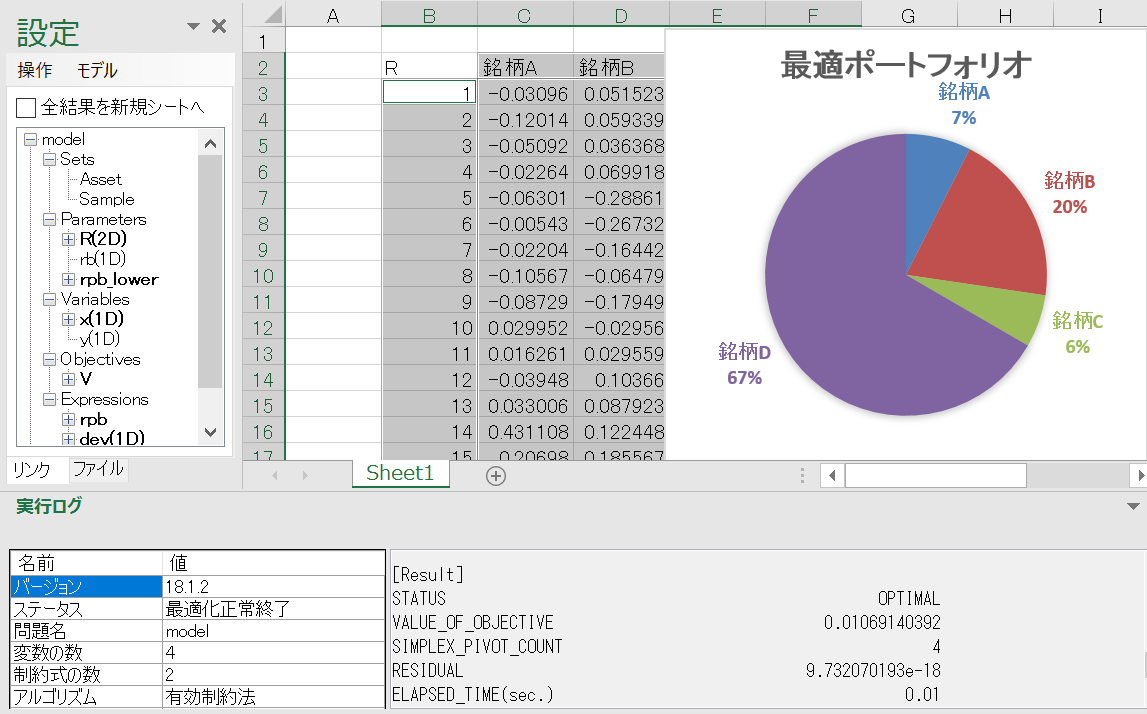
運用・サポート
Web ページにはオンラインマニュアルと数理最適化の応用を網羅した例題集があります。無料のセミナーを毎月開催しているので、初心者の方でも安心して Nuorium Optimizer の使い方を学習できます。
Nuorium Optimizer 及び付属の GUI やモデリング言語はすべて自社開発したものです。Nuorium Optimizer を使ったモデリングや解法の構築といったコンサルティングや特別セミナー、周辺ソフトウェア開発といった受託開発まで可能です。
機能概要
詳細な機能・仕様は パンフレット もご覧ください。
適用範囲
- 線形計画問題 (LP)
- 混合整数線形計画問題 (MILP)
- 凸混合整数二次計画問題 (CMIQP)
- 凸二次計画問題 (CQP)
- 凸計画問題 (CP)
- 非線形計画問題 (NLP)
- 半正定値計画問題 (SDP)
- 非線形半正定値計画問題 (NLSDP)
- 重み付き制約充足問題 (WCSP)
- 資源制約付きスケジューリング問題 (RCPSP)
アルゴリズム
利用できるアルゴリズムはモデリング言語によって異なります。
- 単体法
- 双対単体法
- 有効制約法
- 線形計画問題専用内点法
- 直線探索法
- 準ニュートン法
- 信頼領域内点法
- 直線探索法に基づく逐次二次計画法
- 信頼領域法に基づく逐次二次計画法
- 線形半正定値計画問題に対する主双対内点法
- 信頼領域法を用いた非線形半正定値計画問題に対する主双対内点法
- 制約充足問題ソルバ
- 重み付き局所探索法
- 資源制約付きスケジューリング問題ソルバ
数理最適化問題の記述に特化した独自のモデリング言語を搭載しています。 添字を用いた独自の書式で限界まで簡潔な記述ができます。 C++ ベースの C++SIMPLE、Python ベースの PySIMPLE、Rベースの RSIMPLE をご利用いただけます。 内部の計算エンジンはいずれも同じものです。
C++SIMPLE
(混合整数)線形計画問題、凸(混合整数)二次計画問題、非線形計画問題をシームレスにモデリングし、求解する環境を提供します。
詳細は モデリング言語 C++SIMPLE をご確認ください。
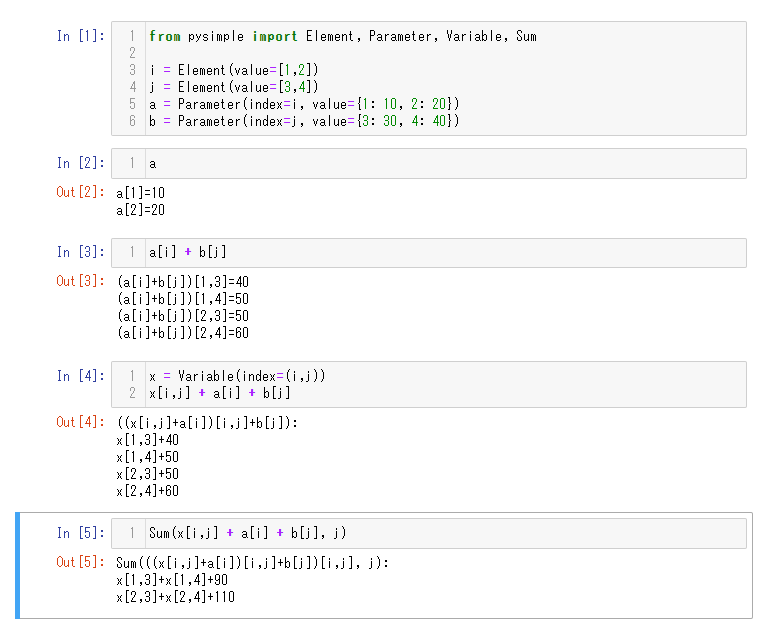
PySIMPLE
PySIMPLE は Nuorium Optimizer の求解ライブラリのうち(混合整数)線形計画問題、凸(混合整数)二次計画問題、二次制約付き二次計画問題、および制約充足問題に対して Nuorium Optimizer への接続インターフェースを提供します。他の問題クラスに対しては C++SIMPLE や RSIMPLE をご利用ください。
詳細は以下をご確認ください。
RSIMPLE
RSIMPLE は統計解析ソフトウェア R をインターフェースとするモデリング言語です。
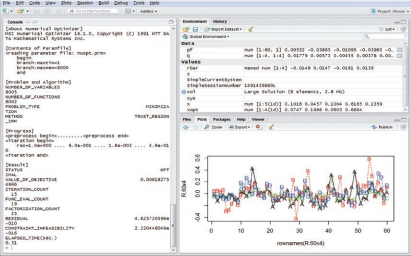
詳細は以下をご確認ください。

詳細は Nuorium Optimizer Excelアドインマニュアル をご確認ください。
FAQ
一覧は Nuorium Optimizer FAQ をご覧ください。
- 純国産の自社開発製品ですのでソルバー内部を熟知しており、開発者自身がコンサルティングやサポート対応いたします。
- 他社製品と比較して幅広い問題クラスに対応し、非常に多彩な求解アルゴリズムを備えています。
- 添字を用いる独自のモデリング言語により限界まで簡潔な記述でモデリングが可能です。
- 統合開発環境 や Excel アドインなど GUI 上からも直感的な操作が可能です。
Nuorium Optimizer をご利用いただくためには次の環境が必要です。
- OS:Windows、macOS、Linux
- CPU:2.0GHz 以上
- メモリ:空きメモリ 1GB 以上(2GB 以上推奨)
- ディスク:空き容量 6GB 以上(11GB 以上推奨)
- CPU アーキテクチャ:x86_64
- パブリッククラウド:AWS、Microsoft Azure など
また、開発に利用するモデリング言語に応じて、対応するプログラミング言語をインストールする必要があります。
詳細は 動作環境 をご確認ください。
資料請求・お問い合わせ
Nuorium Optimizer に関して価格・試用版等の詳しい情報や、お尋ねになりたい点は、お気軽にお問い合わせください。
なお、FAQ にお客様からよく寄せられるご質問をまとめました。お問い合わせの前に、是非一度ご確認ください。