2.12 巡回セールスマン問題
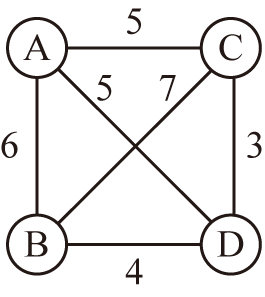
巡回セールスマン問題とは,セールスマンがある都市から出発し,全ての都市を訪問して,出発地点に帰還する場合,どのような順番で都市を回るのが最短経路であるか,という問題です.この問題は最後に訪れる都市が出発地点でなくてもよいという設定もありますが,ここでは,最後に訪れる都市は出発地点であるという設定の問題を紹介します.また,一度訪れた都市を経由して別の都市に移動するような場合は考えないこととします.
この問題をNuorium Optimizerで解くために定式化を行います.本例題の定式化は文献[4]からの引用です.“すべての都市を訪問して出発地点に帰還する”ということは,一筆書きの経路を考えるため,経路のどの都市を出発地点に解釈してもよいことになります.ここでは仮に都市Aを出発地点と解釈することにします.
変数について考えましょう.どの都市からどの都市に移っていくかを決定する問題ですので,ある都市から別のある都市に移動する場合に1をとり,移動しない場合に0をとるような0-1変数,
,
,
,
,
,
,
,
,
,
,
を導入します.例えば,
は都市Aから都市Bに移動する場合に1をとり,移動しない場合には0をとります.
次に,最小化すべき目的関数は経路長になりますので,各都市間の距離を用いて,
と表現することができます.
最後に制約条件です.巡回セールマン問題特有の制約,“すべての都市を訪問して帰還する”を定式化する必要があります.この制約は,“各都市から別都市の1つに移動する”,“各都市に別都市の1つから移動する”という制約を含みます.例えば,都市Aについては,
という制約が必要です.
上記の制約だけでは不十分であり,もう少し制約を加える必要があります.なぜならば,上記の場合には,,
となるような解,つまり一筆書きで全都市を訪問することができないような経路が許されてしまうからです.巡回セールスマン問題では,一筆書きの閉路をツアーと呼び,「都市A→都市B→都市A」のような,すべての都市を訪問していないツアーを特にサブツアーと呼びます.巡回セールスマン問題では,上記制約に加えて“すべてのサブツアーを排除する”という制約が必要になります.この制約を表現するために,中間変数と呼ばれる変数
,
,
を導入し,都市B,都市C,都市Dが関わるツアーを排除するという制約を導入します.この制約は,
と表現することができます.上記制約から,例えば,(1),(3)の制約の両辺を足し合わせると,
となり,,すなわち「都市B→都市C→都市B」のようなサブツアーを排除し,また,(1),(4),(5)の制約の両辺を足し合わせると,
となり,,すなわち,「都市B→都市C→都市D→都市B」のようなサブツアーを排除することができます.都市Aに関する情報が式に現れないのは,解となるツアーまでをも排除しないようにするためです.つまり,都市Aを含むツアーの内,都市A以外で構成されるツアーをすべて排除することを表現しています.
ところで中間変数,
,
は,訪れる都市の順番と考えられます.例えば,都市B→都市Cなる経路を持つ,すなわち
と仮定します.制約式(1)は
を示します.また,(1)~(6)がすべて同一の形をしていることから,
もわかるため,等号
が成立することが導かれます.このようにして,
(
はB, C, Dのいずれか)はステップ幅1をもって全順序が与えられます.次の制約式(7),(8),(9)を導入することで,
は1から始まるように調整できます.このようにして全順序と,都市Aを出発してから再び都市Aに戻ってくるまでの巡回順を一致させることが可能です.
以上のことから,次のように定式化することができます.
| 0-1変数 | |
| 都市Aから都市Bへ移動するか否か | |
| 都市Aから都市Cへ移動するか否か | |
| 都市Aから都市Dへ移動するか否か | |
| 都市Bから都市Cへ移動するか否か | |
| 都市Bから都市Dへ移動するか否か | |
| 都市Cから都市Dへ移動するか否か | |
| 都市Bから都市Aへ移動するか否か | |
| 都市Cから都市Aへ移動するか否か | |
| 都市Dから都市Aへ移動するか否か | |
| 都市Cから都市Bへ移動するか否か | |
| 都市Dから都市Bへ移動するか否か | |
| 都市Dから都市Cへ移動するか否か | |
| 中間変数 | |
| 都市Bを巡回する順番 | |
| 都市Cを巡回する順番 | |
| 都市Dを巡回する順番 | |
| 目的関数(最小化) | |
| 経路長 | |
| 制約 | |
| 都市Aから別都市の1つに移動する | |
| 都市Bから別都市の1つに移動する | |
| 都市Cから別都市の1つに移動する | |
| 都市Dから別都市の1つに移動する | |
| 都市Aに別都市の1つから移動する | |
| 都市Bに別都市の1つから移動する | |
| 都市Cに別都市の1つから移動する | |
| 都市Dに別都市の1つから移動する | |
| サブツアー排除制約 | |
| サブツアー排除制約 | |
| サブツアー排除制約 | |
| サブツアー排除制約 | |
| サブツアー排除制約 | |
| サブツアー排除制約 | |
| 都市Bを訪れる順番の上下限 | |
| 都市Cを訪れる順番の上下限 | |
| 都市Dを訪れる順番の上下限 | |
この問題は,変数に0-1変数と連続変数が混ざっており,目的関数,制約式全てが線形なので,混合整数線形計画問題となります.定式化した結果をC++SIMPLEで記述すると以下のようになります.
// 変数
IntegerVariable x_AB(name = "AtoB", type = binary);
IntegerVariable x_AC(name = "AtoC", type = binary);
IntegerVariable x_AD(name = "AtoD", type = binary);
IntegerVariable x_BC(name = "BtoC", type = binary);
IntegerVariable x_BD(name = "BtoD", type = binary);
IntegerVariable x_CD(name = "CtoD", type = binary);
IntegerVariable x_BA(name = "BtoA", type = binary);
IntegerVariable x_CA(name = "CtoA", type = binary);
IntegerVariable x_DA(name = "DtoA", type = binary);
IntegerVariable x_CB(name = "CtoB", type = binary);
IntegerVariable x_DB(name = "DtoB", type = binary);
IntegerVariable x_DC(name = "DtoC", type = binary);
// 目的関数
Objective route(name = "経路長", type = minimize);
route = 6 * x_AB + 5 * x_AC + 5 * x_AD + 7 * x_BC + 4 * x_BD + 3 * x_CD +
6 * x_BA + 5 * x_CA + 5 * x_DA + 7 * x_CB + 4 * x_DB + 3 * x_DC;
// 中間変数
Variable y_B;
Variable y_C;
Variable y_D;
// 各都市から別都市の 1 つに移動する
x_AB + x_AC + x_AD == 1;
x_BA + x_BC + x_BD == 1;
x_CA + x_CB + x_CD == 1;
x_DA + x_DB + x_DC == 1;
// 各都市に別都市の 1 つから移動する
x_BA + x_CA + x_DA == 1;
x_AB + x_CB + x_DB == 1;
x_AC + x_BC + x_DC == 1;
x_AD + x_BD + x_CD == 1;
// サブツアーを排除する
y_B - y_C + 3 * x_BC <= 2;
y_B - y_D + 3 * x_BD <= 2;
y_C - y_B + 3 * x_CB <= 2;
y_C - y_D + 3 * x_CD <= 2;
y_D - y_B + 3 * x_DB <= 2;
y_D - y_C + 3 * x_DC <= 2;
// 各都市を通る順番は出発地点を除く都市数以下
1<=y_B<=3;
1<=y_C<=3;
1<=y_D<=3;
// 求解
solve();
// 出力
x_AB.val.print();
x_AC.val.print();
x_AD.val.print();
x_BC.val.print();
x_BD.val.print();
x_CD.val.print();
x_BA.val.print();
x_CA.val.print();
x_DA.val.print();
x_CB.val.print();
x_DB.val.print();
x_DC.val.print();より汎用的に問題を定式化すると以下のようになります.
| 集合 | |
| 都市の集合 | |
| 出発地点以外の都市の集合 | |
| 定数 | |
| 都市 |
|
| 集合 |
|
| 0-1変数 | |
| 都市 |
|
| 中間変数 | |
| 都市 |
|
| 目的関数(最小化) | |
| 経路長 | |
| 制約 | |
| 都市 |
|
| 都市 |
|
| サブツアーを排除 | |
| 都市 |
|
次に,定数(各都市間の距離)をデータファイルから与えるC++SIMPLEモデルを示します.このようにモデルとデータを分離することにより,都市数が変わったとしてもデータファイルを変更するだけで対応できるようになります.
// 集合と添字 Set City(name = "都市"); Element c1(set = City); Element c2(set = City); Set City_(name = "出発地点を除く都市"); Element c_(set = City_); Element c1_(set = City_); Element c2_(set = City_); // パラメータ Parameter dis(name = "距離", index = (c1, c2)); Parameter num = City_.card(); // 変数 IntegerVariable x(name = "移動", index = (c1, c2), type = binary); Variable y(name = "順番", index = c_); // 目的関数 Objective route(name = "経路長", type = minimize); route = sum(x[c1, c2] * dis[c1, c2], ((c1, c2), c1 != c2)); // 各都市から 1 つの別都市へ移動する sum(x[c1, c2], (c2, c1 != c2)) == 1; // 各都市に 1 つの別都市から移動する sum(x[c1, c2], (c1, c1 != c2)) == 1; // サブツアーを排除する y[c1_] - y[c2_] + num * x[c1_, c2_] <= num - 1, c1_ != c2_; // 順番の上下限制約 1 <= y[c_] <= num; // 求解 solve(); // 結果出力 x.val.print(); y.val.print(); route.val.print();
データファイル(.dat形式)は以下のようになります.
都市 = A B C D; 出発地点を除く都市 = B C D; 距離 = [A, B] 6 [A, C] 5 [A, D] 5 [B, C] 7 [B, D] 4 [C, D] 3 [B, A] 6 [C, A] 5 [D, A] 5 [C, B] 7 [D, B] 4 [D, C] 3 ;
このモデルを実行すると,,
,
となり,都市A→都市C→都市D→都市B→都市Aの順番で移動するのが最適解となります注1.その経路長は18であることがわかります.
ここからは,やや上級者向けの説明です.先の説明では,変数は全ての都市と都市の間で定義されていました.しかしながら,この変数の立て方は冗長です.これを減らすことにより,さらに効率の良いモデルにすることができます.具体的には,変数
は「異なる都市間」だけで定義すれば十分で同じ都市間の変数
は不要です.
以下は具体的なモデル例です.変数は二次元の集合
上で定義されています.このようにすることにより変数
の数は「都市の数」だけ削減できています.
// 集合と添字 Set City(name = "都市"); Element c1(set = City); Element c2(set = City); Set City_(name = "出発地点を除く都市"); Element c_(set = City_); Element c1_(set = City_); Element c2_(set = City_); Set CityToCity(dim=2); CityToCity = setOf( (c1, c2), c1 != c2 ); Element c12(set=CityToCity); // パラメータ Parameter dis(name = "距離", index = (c1, c2)); Parameter num = City_.card(); // 変数 IntegerVariable x(name = "移動", index = c12, type = binary); Variable y(name = "順番", index = c_); // 目的関数 Objective route(name = "経路長", type = minimize); route = sum(x[c12] * dis[c12], c12); // 各都市から 1 つの別都市へ移動する sum(x[c1, c2], (c2, (c1, c2) < CityToCity)) == 1; // 各都市に 1 つの別都市から移動する sum(x[c1, c2], (c1, (c1, c2) < CityToCity)) == 1; // サブツアーを排除する y[c1_] - y[c2_] + num * x[c1_, c2_] <= num - 1, (c1_, c2_) < CityToCity; // 順番の上下限制約 1 <= y[c_] <= num; // 求解 solve(); // 結果出力 x.val.print(); y.val.print(); route.val.print();
注1)環境によっては逆回りに移動する解が出力されることがあります.
上に戻る