数理最適化セミナーのご案内

2.22 ロバストポートフォリオ最適化問題

　ポートフォリオのリスクを投資対象の収益率の分散共分散行列を用いて計測するマルコビッツモデルにおいて，与えられた分散共分散行列は，しばしば不確実性を伴います．この不確実性に対してロバストな解を得る以下の問題を考えます．

　以下の典型的な平均・分散モデルを考えます．

\begin{equation} \begin{array}{@{}l@{}} \displaystyle \max_x \mu^T x - \lambda x^T\Sigma x \\ s.t.\quad x^T e = 1 \end{array}\end{equation}

　ここで，$\mu$を期待リターン，$\Sigma$をリターンの分散共分散行列，$x$をポートフォリオの重み，$\lambda$をリスク回避係数とします．

　分散共分散行列$\Sigma$に不確実性が伴うとして，以下のロバストポートフォリオ最適化問題を考えます．なお${\rm U}_{\Sigma}$は，不確実性が伴うことによって取りうる$\Sigma$に関する行列の集合とします．

\begin{equation} \begin{array}{@{}l@{}} \displaystyle \max_x \left\{ \mu^T x - \lambda \max_{\Sigma \in {\rm U}_\Sigma} \left\{ x^T \Sigma x \right\} \right\} \\ s.t.\quad x^T e = 1 \end{array} \end{equation}

　${\rm U}_\Sigma$として，分散共分散行列$\Sigma$の各要素が

\[ \underline{\Sigma} \le \Sigma \le \overline{\Sigma}\]

のような区間を持つとします．このとき(2)は，新たに行列$U, L$を用いて以下のような問題に置き換えることができます[6]．なお行列A，Bに対し，$A \bullet B$は，AとBの内積を表すものとします．

\begin{equation} \begin{array}{@{}l@{}} \displaystyle \max_x \mu^T x - \lambda \left( \overline{\Sigma} \bullet U - \underline{\Sigma} \bullet L \right) \\ \begin{array}{@{}l@{\quad}l@{}} s.t. & x^T e = 1 \\ & \left( \begin{array}{cc} U - L & x \\ x^T & 1 \end{array} \right) \succeq 0 \\ & U \ge 0, L \ge 0 \end{array} \end{array} \end{equation}

例題

　分散共分散行列$\Sigma$の各要素の下限を表す行列$sigL$，上限を表す行列$sigU$が以下のように与えられているとき，上記(3)を解きなさい．

　ただし，$\lambda =1$，$\mu^{T} = (0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1)$とします．

　この問題を定式化すると以下のようになります．

集合
$A = \{ 1, 2, \ldots, 8 \}$ 投資対象の集合
　
定数
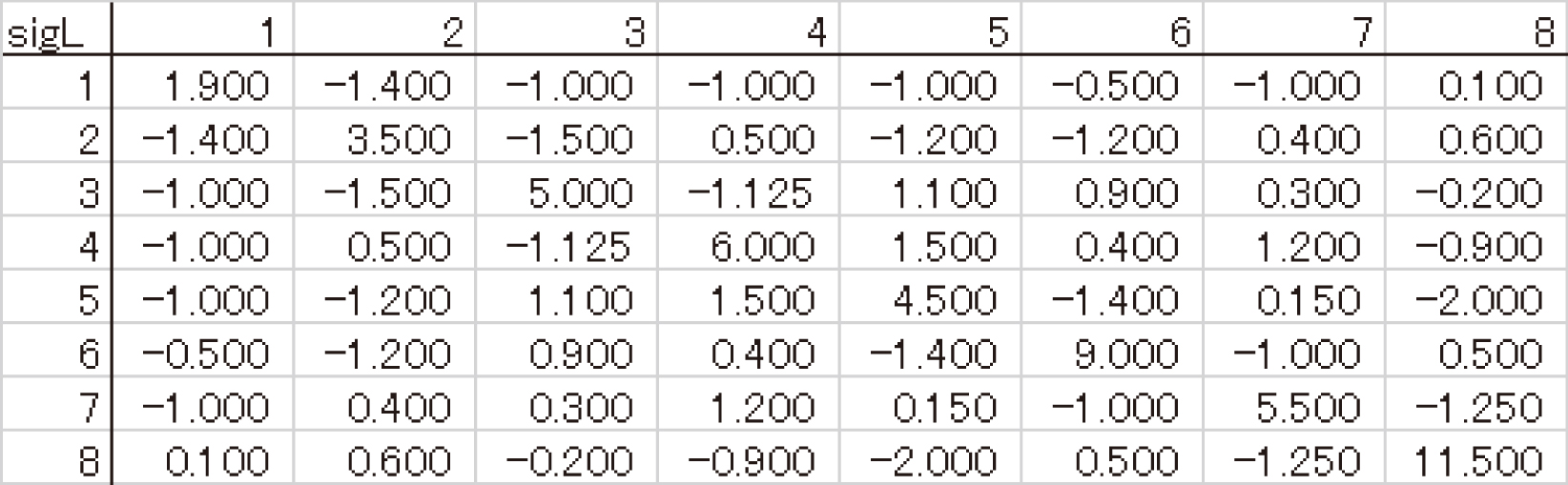
$sigL_{ij}, i \in A, j \in A$ 分散共分散行列の各要素の下限
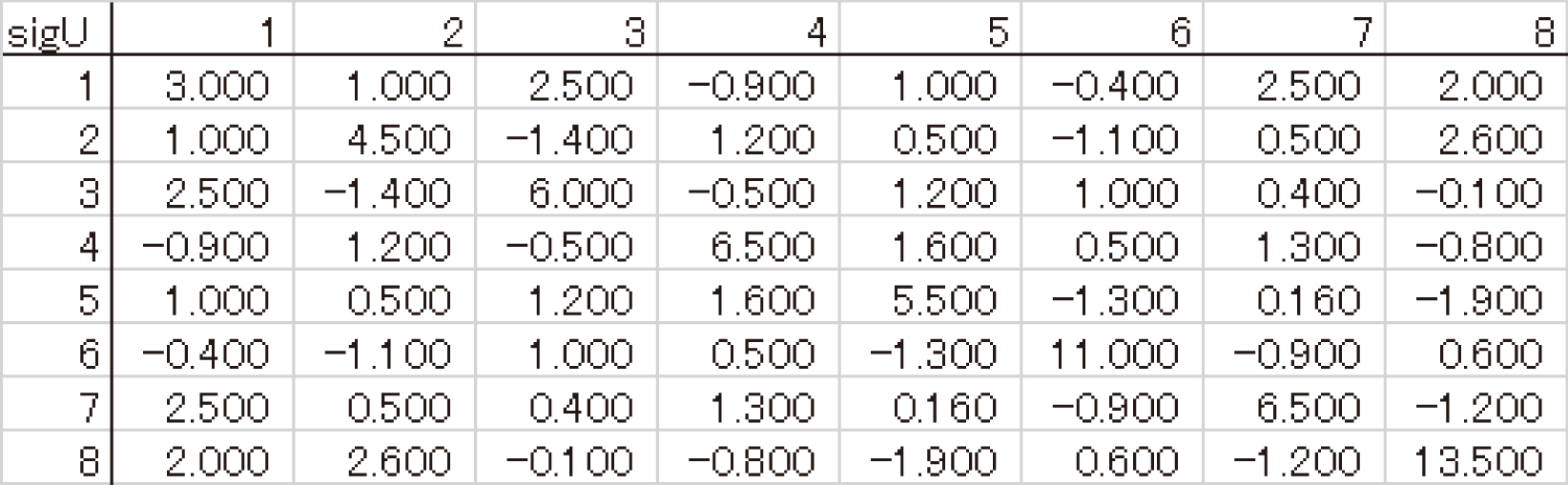
$sigU_{ij}, i \in A, j \in A$ 分散共分散行列の各要素の上限
$\lambda$ リスク回避係数
$\mu_i, i \in A$ 各投資対象の平均収益率
　
変数
$x_i, i \in A$ 組入比率
$L_{ij}, i \in A, j \in A$ 　
$U_{ij}, i \in A, j \in A$ 　
　
目的関数（最大化）
$\mu^T x - \lambda (sigU \bullet U - sigL \bullet L)$ $\bullet$は要素ごとの積の和
　
制約条件
$\left( \begin{array}{cc} U - L & x \\ x^T & 1 \end{array} \right) \succeq 0$ 半正定値制約
$\displaystyle \sum_{i \in A} x_i = 1$ 組入比率の総和は1
$L_{ij} \ge 0, \forall i\in A, j\in A$ 行列$L$の各要素に関する非負条件
$U_{ij} \ge 0, \forall i\in A, j\in A$ 行列$U$の各要素に関する非負条件

　この問題は半正定値制約が入っているので，半正定値計画問題になります．定式化した結果をC++SIMPLEで記述すると以下のようになります．

// 集合と添字
Parameter nA; // 銘柄数
Sequence Asset(from = 1, to = nA);
Element i(set = Asset);
Element j(set = Asset);

// パラメータ
Parameter sigL(index = (i, j));
Parameter sigU(index = (i, j));
Parameter lambda;
Parameter mu(index = i);

// 変数
Variable U(index = (i, j));
Variable L(index = (i, j));
Variable x(index = i);

// 対称行列
Sequence V(from = 1, to = nA + 1);
Element v(set = V);
Element w(set = V);
SymmetricMatrix M((v, w)); 

// M の要素の定義（上三角部分のみ）
M[i, j] = U[i, j] - L[i, j], i <= j; // 左上（の上三角部分）
M[j, nA + 1] = x[j];                 // 右上
M[nA + 1, nA + 1] = 1;               // 右下

// 目的関数
Objective f(type = maximize);
f = sum(mu[i] * x[i], i) - lambda * sum(sigU[i, j] * U[i, j] - sigL[i, j] * L[i, j], (i, j));

// 制約条件
M >= 0; // 半正定値制約
sum(x[i], i) == 1;
U[i, j] == U[j, i], i > j;
L[i, j] == L[j, i], i > j;
U[i, j] >= 0;
L[i, j] >= 0;

// 求解
solve();

// 結果出力
x.val.print();

　データファイルは以下の三つです．

sigL, 1, 2, 3, 4, 5, 6, 7, 8
1, 1.9, -1.4, -1, -1, -1, -0.5, -1, 0.1
2, -1.4, 3.5, -1.5, 0.5, -1.2, -1.2, 0.4, 0.6
3, -1, -1.5, 5, -1.125, 1.1, 0.9, 0.3, -0.2
4, -1, 0.5, -1.125, 6, 1.5, 0.4, 1.2, -0.9
5, -1, -1.2, 1.1, 1.5, 4.5, -1.4, 0.15, -2
6, -0.5, -1.2, 0.9, 0.4, -1.4, 9, -1, 0.5
7, -1, 0.4, 0.3, 1.2, 0.15, -1, 5.5, -1.25
8, 0.1, 0.6, -0.2, -0.9, -2, 0.5, -1.25, 11.5
sigU, 1, 2, 3, 4, 5, 6, 7, 8
1, 3, 1, 2.5, -0.9, 1, -0.4, 2.5, 2
2, 1, 4.5, -1.4, 1.2, 0.5, -1.1, 0.5, 2.6
3, 2.5, -1.4, 6, -0.5, 1.2, 1, 0.4, -0.1
4, -0.9, 1.2, -0.5, 6.5, 1.6, 0.5, 1.3, -0.8
5, 1, 0.5, 1.2, 1.6, 5.5, -1.3, 0.16, -1.9
6, -0.4, -1.1, 1, 0.5, -1.3, 11, -0.9, 0.6
7, 2.5, 0.5, 0.4, 1.3, 0.16, -0.9, 6.5, -1.2
8, 2, 2.6, -0.1, -0.8, -1.9, 0.6, -1.2, 13.5
nA = 8;
lambda = 1;
mu = [1] 0.1 [2] 0.1 [3] 0.1 [4] 0.1 [5] 0.1 [6] 0.1 [7] 0.1 [8] 0.1;

　このモデルを実行すると以下のような解が得られます．

x[1] = 1.86393e-06
x[2] = 0.233168
x[3] = 0.175305
x[4] = 0.0633979
x[5] = 0.171047
x[6] = 0.131893
x[7] = 0.152883
x[8] = 0.0723034
2.21 相関行列取得問題
2.23 最大カット問題

 

 

上に戻る