数理最適化セミナーのご案内

2.13.3 仕事割当問題

　ここでは，仕事を人に効率よく割り当てる問題を取り上げます．次の例題を考えます．

例題

　「安藤」「佐藤」「鈴木」「山本」「渡辺」の5人に仕事を割り当てます．仕事は「接客」「厨房」「レジ打ち」「発注」「ごみ捨て」「買出し」「掃除」「仕込み」の8つです．各人を仕事に割り当てるにはコストがかかり，それは個人・仕事によって決まります．また，各人はそれぞれの仕事に対して熟練度があり，熟練度が高いほどコストがかかる傾向があります．以下は熟練度とコストをまとめたものです．

熟練度 安藤 佐藤 鈴木 山本 渡辺
接客 -1 3 -2 3 -4
厨房 5 -2 3 -4 5
レジ打ち 0 3 -2 3 -1
発注 -3 -1 1 1 2
ごみ捨て 1 -1 3 1 -1
買出し -1 -1 1 0 2
掃除 2 -2 2 -3 4
仕込み 5 -2 0 1 5

　

コスト 安藤 佐藤 鈴木 山本 渡辺
接客 570 1400 520 1410 450
厨房 1800 1000 1700 1050 2300
レジ打ち 800 1500 500 1500 600
発注 500 600 1000 1000 1200
ごみ捨て 800 600 1200 800 600
買出し 600 600 800 700 1300
掃除 1200 500 1200 500 1300
仕込み 1500 1000 1200 1200 1500

　

　また，以下の点を守らなくてはいけません．

  • 各人に割り振る仕事は，最大で3つまでとする．
  • 「接客」「厨房」「レジ打ち」「掃除」「仕込み」は2人を割り当てる．
  • 「発注」「ごみ捨て」「買出し」は1人を割り当てる．
  • 「接客」「厨房」は別の人が担当する．
  • 各仕事において，仕事を担当する人の熟練度の和を，その仕事のクオリティーとする．
  • 各仕事のクオリティーは負になってはいけない．

　このとき，コストの合計を最小にするような割り当て方を求めてください．

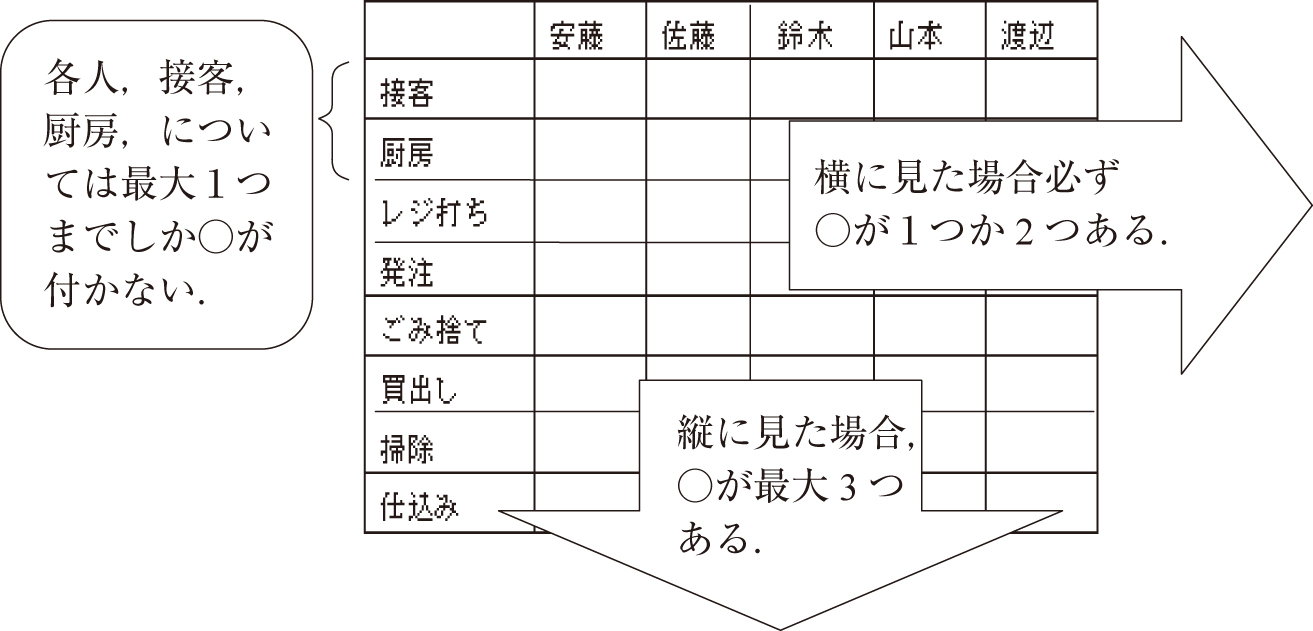
　この問題も前節の問題と同様に以下のようなマス目に○をつける問題として考えることができます．

　以上を踏まえて，以下のように定式化することができます．

集合
$JOB = \{接客, 厨房, レジ打ち, 発注, ごみ捨て, 買出し, 掃除, 仕込み\}$ 仕事の集合
$PEOPLE = \{安藤, 佐藤, 鈴木, 山本, 渡辺\}$ 人の集合
　
0-1変数
$x_{jp}, j \in JOB, p \in PEOPLE$ 仕事$j$を人$p$に割り当てるならば$x_{jp} = 1$，そうでないならば$x_{jp} = 0$とする
　
定数
$cost_{jp}, j \in JOB, p \in PEOPLE$ 仕事$j$を人$p$に割り当てる際のコスト
$jyukuren_{jp}, j \in JOB, p \in PEOPLE$ 仕事$j$を人$p$が行う際の熟練度
　
目的関数（最小化）
$\displaystyle \sum_{j, p} cost_{jp} \times x_{jp}$ コストの総和
　
制約条件
$\displaystyle \sum_p x_{jp} = 2, \forall j \in \{接客, 厨房, レジ打ち, 掃除, 仕込み\}$ 「接客」「厨房」「レジ打ち」「掃除」「仕込み」は2人を割り当てる．
$\displaystyle \sum_p x_{jp} = 1, \forall j \in \{発注, ごみ捨て, 買出し\}$ 「発注」「ごみ捨て」「買出し」は1人を割り当てる．
$\displaystyle \sum_j x_{jp} \le 3, \forall p \in PEOPLE$ 各人には，最大3つまでの仕事を割り当てることができる
$\displaystyle \sum_p jyukuren_{jp} \times x_{jp} \ge 0, \forall j \in JOB$ 各仕事のクオリティーが負になってはいけない
$\displaystyle \sum_{j, j \in \{接客, 厨房\}} x_{jp} \le 1, \forall p \in PEOPLE$ 接客，厨房は違う人が担当する（同じ人が接客と厨房を兼ねない）．

　今回は定数に関してはファイルからデータを与えてみます．モデル部分は以下のようになります．

// 集合と添字
Set Job;
Element j(set = Job);
Set People;
Element p(set = People);

// パラメータ
Parameter cost(index = (j, p), name = "コスト");
Parameter jyukuren(index = (j, p), name = "熟練度");

// 変数
IntegerVariable x(type = binary, index = (j, p));

// 目的関数
Objective total_cost(type = minimize, name = "総コスト");
total_cost = sum(cost[j, p] * x[j, p], (j, p));

// 制約条件
sum(x[j, p], p) == 2, j == "接客" || j == "厨房" || j == "レジ打ち" || j == "掃除" || j == "仕込み";
sum(x[j, p], p) == 1, j == "発注" || j == "ごみ捨て" || j == "買出し";
sum(x[j, p], j) <= 3;
sum(x[j, p] * jyukuren[j, p], p) >= 0;
sum(x[j, p], (j, j == "接客" || j == "厨房")) <= 1;

// 求解
solve();

// 結果出力
total_cost.val.print();
simple_printf("%s, %s\n", j, p, x[j, p].val == 1);
simple_printf("\n");
simple_printf("%sのクオリティーは %d\n", j, sum(jyukuren[j, p] * x[j, p], p));

　以下がcsv形式の入力ファイルです．コストに関してと熟練度に関しての二種類のファイルを用意する必要があります．

熟練度, 安藤, 佐藤, 鈴木, 山本, 渡辺
接客, -1, 3, -2, 3, -4
厨房, 5, -2, 3, -4, 5
レジ打ち, 0, 3, -2, 3, -1
発注, -3, -1, 1, 1, 2
ごみ捨て, 1, -1, 3, 1, -1
買出し, -1, -1, 1, 0, 2
掃除, 2, -2, 2, -3, 4
仕込み, 5, -2, 0, 1, 5
コスト, 安藤, 佐藤, 鈴木, 山本, 渡辺
接客, 570, 1400, 520, 1410, 450
厨房, 1800, 1000, 1700, 1050, 2300
レジ打ち, 800, 1500, 500, 1500, 600
発注, 500, 600, 1000, 1000, 1200
ごみ捨て, 800, 600, 1200, 800, 600
買出し, 600, 600, 800, 700, 1300
掃除, 1200, 500, 1200, 500, 1300
仕込み, 1500, 1000, 1200, 1200, 1500

　このモデルをNuorium Optimizerで実行すると，最後に

総コスト = 13380
ごみ捨て, 安藤
レジ打ち, 佐藤
レジ打ち, 渡辺
仕込み, 山本
仕込み, 鈴木
厨房, 佐藤
厨房, 鈴木
接客, 安藤
接客, 山本
掃除, 安藤
掃除, 佐藤
買出し, 山本
発注, 鈴木

ごみ捨てのクオリティーは 1
レジ打ちのクオリティーは 2
仕込みのクオリティーは 1
厨房のクオリティーは 1
接客のクオリティーは 2
掃除のクオリティーは 0
買出しのクオリティーは 0
発注のクオリティーは 1

という表示がされ，この例題の答えを確認できます．

例題

　先ほどの問題に以下の条件を付け加えてください．

　

　安藤に「接客」をさせることはできない

　佐藤に「厨房」をさせることはできない

　鈴木に「レジ打ち」をさせることはできない

　山本に「発注」をさせることはできない

　渡辺に「ごみ捨て」をさせることはできない

　さて，この問題ですが通常に考えると先ほどの問題に以下の制約を付け加えることで解くことができます．また記述する位置はxの宣言以降，solve()の手前であればどこでもかまいません．

x["接客, 安藤"] == 0; 
x["厨房, 佐藤"] == 0; 
x["レジ打ち, 鈴木"] == 0; 
x["発注, 山本"] == 0; 
x["ごみ捨て, 渡辺"] == 0;

　上記記述を追加し，モデルを実行すると結果は以下のように変わります．

総コスト = 13470
ごみ捨て, 安藤
レジ打ち, 佐藤
レジ打ち, 渡辺
仕込み, 山本
仕込み, 鈴木
厨房, 安藤
厨房, 山本
接客, 佐藤
接客, 鈴木
掃除, 安藤
掃除, 佐藤
買出し, 山本
発注, 鈴木

ごみ捨てのクオリティーは 1
レジ打ちのクオリティーは 2
仕込みのクオリティーは 1
厨房のクオリティーは 1
接客のクオリティーは 1
掃除のクオリティーは 0
買出しのクオリティーは 0
発注のクオリティーは 1

　結果を見ると，総コストが多くなっていることが分かります．

　以上の考え方は以下の図のように変数を準備し，色が付いているところが0であるという制約を設けたと考えることができます．（なお図中のレジはレジ打ち，ごみはごみ捨て，買出は買出し，仕込は仕込みです）

  安藤 佐藤 鈴木 山本 渡辺
接客 x[接客，安藤] x[接客，佐藤] x[接客，鈴木] x[接客，山本] x[接客，渡辺]
厨房 x[厨房，安藤] x[厨房，佐藤] x[厨房，鈴木] x[厨房，山本] x[厨房，渡辺]
レジ打ち x[レジ，安藤] x[レジ，佐藤] x[レジ，鈴木] x[レジ，山本] x[レジ，渡辺]
発注 x[発注，安藤] x[発注，佐藤] x[発注，鈴木] x[発注，山本] x[発注，渡辺]
ごみ捨て x[ごみ，安藤] x[ごみ，佐藤] x[ごみ，鈴木] x[ごみ，山本] x[ごみ，渡辺]
買出し x[買出，安藤] x[買出，佐藤] x[買出，鈴木] x[買出，山本] x[買出，渡辺]
掃除 x[掃除，安藤] x[掃除，佐藤] x[掃除，鈴木] x[掃除，山本] x[掃除，渡辺]
仕込み x[仕込，安藤] x[仕込，佐藤] x[仕込，鈴木] x[仕込，山本] x[仕込，渡辺]

　

　ここで，上の図の色のついている部分は1になることがないので，はじめから変数を準備する必要がないと考えることが出来ます．特に大規模の割当問題においては，無駄な変数を準備することにより不用意に問題の規模を大きくしてしまうと，計算のパフォーマンスを著しく低下させてしまう要因になります．ここでは明らかな制約に関しては「制約を付け加えることなく，そのような選択肢を元々準備しない」という方法を紹介します．以下の図のようなイメージです．

  安藤 佐藤 鈴木 山本 渡辺
接客   x[接客，佐藤] x[接客，鈴木] x[接客，山本] x[接客，渡辺]
厨房 x[厨房，安藤]   x[厨房，鈴木] x[厨房，山本] x[厨房，渡辺]
レジ打ち x[レジ，安藤] x[レジ，佐藤]   x[レジ，山本] x[レジ，渡辺]
発注 x[発注，安藤] x[発注，佐藤] x[発注，鈴木]   x[発注，渡辺]
ごみ捨て x[ごみ，安藤] x[ごみ，佐藤] x[ごみ，鈴木] x[ごみ，山本]  
買出し x[買出，安藤] x[買出，佐藤] x[買出，鈴木] x[買出，山本] x[買出，渡辺]
掃除 x[掃除，安藤] x[掃除，佐藤] x[掃除，鈴木] x[掃除，山本] x[掃除，渡辺]
仕込み x[仕込，安藤] x[仕込，佐藤] x[仕込，鈴木] x[仕込，山本] x[仕込，渡辺]

　

　定式化する際に，上記を表す集合$JPPair$を準備する必要があります．

  • $(j, p) \in JPPair \Leftrightarrow \mbox{$j$を$p$に割り当てることができる}$

　以下が$JPPair$を用いた定式化です．

集合
$JOB = \{接客, 厨房, レジ打ち, 発注, ごみ捨て, 買出し, 掃除, 仕込み\}$ 仕事の集合，$j \in JOB$
$PEOPLE = \{安藤, 佐藤, 鈴木, 山本, 渡辺\}$ 人の集合，$p \in PEOPLE$
$(j, p) \in JPPair \Leftrightarrow jをpに割り当てることができる$ 　
　
0-1変数
$x_{jp}, (j, p) \in JPPair$ 仕事$j$を人$p$に割り当てるならば$x_{jp} = 1$，そうでないならば$x_{jp} = 0$とする
　
定数
$cost_{jp}, (j, p) \in JPPair$ 仕事$j$を人$p$に割り当てる際のコスト
$jyukuren_{jp}, (j, p) \in JPPair$ 仕事$j$を人$p$が行う際の熟練度
　
目的関数（最小化）
$\displaystyle \sum_{j, p, (j, p) \in JPPair} cost_{jp} \times x_{jp}$ コストの総和
　
制約条件
$\displaystyle \sum_{p, (j, p) \in JPPair} x_{jp} = 2, \forall j \in \{接客, 厨房, レジ打ち, 掃除, 仕込み\}$ 「接客」「厨房」「レジ打ち」「掃除」「仕込み」は2人を割り当てる．
$\displaystyle \sum_{p, (j, p) \in JPPair} x_{jp} = 1,\forall j \in \{発注, ごみ捨て, 買出し\}$ 「発注」「ごみ捨て」「買出し」は1人を割り当てる
$\displaystyle \sum_{j, (j, p) \in JPPair} x_{jp} \le 3$ 各人には，最大3つまで仕事を割り当てることができる
$\displaystyle \sum_{p, (j, p) \in JPPair} jyukuren_{jp} \times x_{jp} \ge 0$ 各仕事のクオリティーが負になってはいけない
$\displaystyle \sum_{(j, p), j \in \{接客, 厨房\}, (j, p) \in JPPair} x_{jp} \le 1$ 接客，厨房は違う人が担当する．

　モデルは以下のようになります．

// 集合と添字
Set Job;
Element j(set = Job);
Set People;
Element p(set = People);
Set JPPair(dim = 2, superSet = (Job, People));
Element jp(set = JPPair);

// パラメータ
Parameter cost(index = jp, name = "コスト");
Parameter jyukuren(index = jp, name = "熟練度");

// 変数
IntegerVariable x(type = binary, index = jp);

// 目的関数
Objective total_cost(type = minimize, name = "総コスト");
total_cost = sum(cost[j, p] * x[j, p], (j, p, (j, p) < JPPair));

// 制約条件
sum(x[j, p], (p, (j, p) < JPPair)) == 2, j == "接客" || j == "厨房" || j == "レジ打ち" || j == "掃除" || j == "仕込み";
sum(x[j, p], (p, (j, p) < JPPair)) == 1, j == "発注" || j == "ごみ捨て" || j == "買出し";
sum(x[j, p], (j, (j, p) < JPPair)) <= 3;
sum(x[j, p] * jyukuren[j, p], (p, (j, p) < JPPair)) >= 0;
sum(x[j, p], (j, (j, p) < JPPair, j == "接客" || j == "厨房")) <= 1;

// 求解
solve();

// 結果出力
total_cost.val.print();
simple_printf("%s, %s\n", jp.at(1), jp.at(2), x[jp].val == 1);
simple_printf("\n");
simple_printf("%sのクオリティーは %d\n", j, sum(jyukuren[j, p] * x[j, p], (p, (j, p) < JPPair)));

　上記記述内のJPPairには無駄な[j, p]のペアを入れてはいけないので，入力ファイルもそれに伴い以下のように変わります．

j, p, 熟練度, コスト
接客, 佐藤, 3, 1400
接客, 鈴木, -2, 520
接客, 山本, 3, 1410
接客, 渡辺, -4, 450
厨房, 安藤, 5, 1800
厨房, 鈴木, 3, 1700
厨房, 山本, -4, 1050
厨房, 渡辺, 5, 2300
レジ打ち, 安藤, 0, 800
レジ打ち, 佐藤, 3, 1500
レジ打ち, 山本, 3, 1500
レジ打ち, 渡辺, -1, 600
発注, 安藤, -3, 500
発注, 佐藤, -1, 600
発注, 鈴木, 1, 1000
発注, 渡辺, 2, 1200
ごみ捨て, 安藤, 1, 800
ごみ捨て, 佐藤, -1, 600
ごみ捨て, 鈴木, 3, 1200
ごみ捨て, 山本, 1, 800
買出し, 安藤, -1, 600
買出し, 佐藤, -1, 600
買出し, 鈴木, 1, 800
買出し, 山本, 0, 700
買出し, 渡辺, 2, 1300
掃除, 安藤, 2, 1200
掃除, 佐藤, -2, 500
掃除, 鈴木, 2, 1200
掃除, 山本, -3, 500
掃除, 渡辺, 4, 1300
仕込み, 安藤, 5, 1500
仕込み, 佐藤, -2, 1000
仕込み, 鈴木, 0, 1200
仕込み, 山本, 1, 1200
仕込み, 渡辺, 5, 1500

　またこのモデルを制約充足問題ソルバwcspを用いる場合にはモデルを以下のように変更する必要があります．

// 集合と添字
Set Job;
Element j(set = Job);
Set People;
Element p(set = People);
Set JPPair(dim = 2, superSet = (Job, People));
Element jp(set = JPPair);

// パラメータ
Parameter cost(index = jp, name = "コスト");
Parameter jyukuren(index = jp, name = "熟練度");

// 変数
IntegerVariable x(type = binary, index = jp);

// 目的関数
Objective total_cost(type = minimize, name = "総コスト");
total_cost = sum(cost[j, p] * x[j, p], (j, p, (j, p) < JPPair));

// 制約条件
sum(x[j, p], (p, (j, p) < JPPair)) == 2, j == "接客" || j == "厨房" || j == "レジ打ち" || j == "掃除" || j == "仕込み";
selection(x[j, p], (p, (j, p) < JPPair)), j == "発注" || j == "ごみ捨て" || j == "買出し"; // wcsp 特有の関数 selection
sum(x[j, p], (j, (j, p) < JPPair)) <= 3;
sum(x[j, p] * jyukuren[j, p], (p, (j, p) < JPPair)) >= 0;
sum(x[j, p], (j, (j, p) < JPPair, j == "接客" || j == "厨房")) <= 1;

// 求解
options.method = "wcsp"; // 解法に wcsp を用いる指定
options.maxtim = 10; // 計算時間の設定
solve();

// 結果出力
total_cost.val.print();
simple_printf("%s, %s\n", jp.at(1), jp.at(2), x[jp].val == 1);
simple_printf("\n");
simple_printf("%sのクオリティーは %d\n", j, sum(jyukuren[j, p] * x[j, p], (p, (j, p) < JPPair)));

　大規模な割当問題を解く際の問題規模に対する対応として上記で紹介した手法を試してみてください．

2.13.2 基礎的なマス埋め割当問題
2.14 二次割当問題

 

 

上に戻る