2.21 相関行列取得問題
複数の株価の時系列データ等,相関を持った乱数列を発生させる際に,元の相関行列内の要素をある程度任意に変更したい場合があります.しかし,相関を持った乱数列を適切に発生させるためには,相関行列は半正定値である必要があります.そこで,与えられた行列に一番近く,かつ,半正定値であるような相関行列を作成する問題を考えます.
この問題を定式化すると以下のようになります.
| 集合 | |
| 相関行列の行及び列の集合 | |
| 定数 | |
| 所与の行列の要素 | |
| 相関行列の最小固有値 | |
| 変数 | |
| 相関行列の要素 | |
| 目的関数(最小化) | |
| 元の行列と相関行列の差のフロベニウスノルムの二乗 | |
| 制約条件 | |
| 半正定値制約 | |
| 対角要素は1 | |
この問題は半正定値制約が入っているので,半正定値計画問題になります.
定式化した結果をC++SIMPLEで記述すると以下のようになります.なお,ここでは相関行列の最小固有値minEigをとしています.
// 集合と添字
OrderedSet N;
Element i(set = N), j(set = N);
// パラメータ
Parameter A(index = (i, j)); // 与えられた行列の要素
Parameter minEig = 1.0e-3; // 出力される相関行列の最小固有値
// 変数
Variable X(index = (i, j));
// 対称行列
SymmetricMatrix M((i, j));
M[i, j] = X[i, j], i <= j; // 上三角部分のみ定義
// 目的関数
Objective diffnrm(type = minimize); // 差の行列のノルム
diffnrm = sum((X[i, j] - A[i, j]) * (X[i, j] - A[i, j]), (i, j));
// 制約条件
M >= minEig; // 半正定値制約
X[j, i] == X[i, j], i < j; // X は対称行列
X[i, i] == 1; // 対角要素は 1
// 求解
solve();
// 結果出力(CSV 形式)
simple_printf(" X");
simple_printf(",%5d", i);
simple_printf("\n");
Element i_tmp;
for(i_tmp = N.first(); i_tmp < N; i_tmp = N.next(i_tmp)){
simple_printf("%2d", i_tmp);
simple_printf(",%5.2f", X[i_tmp, j]);
simple_printf("\n");
}データファイル(.csv形式)は以下のようになります.
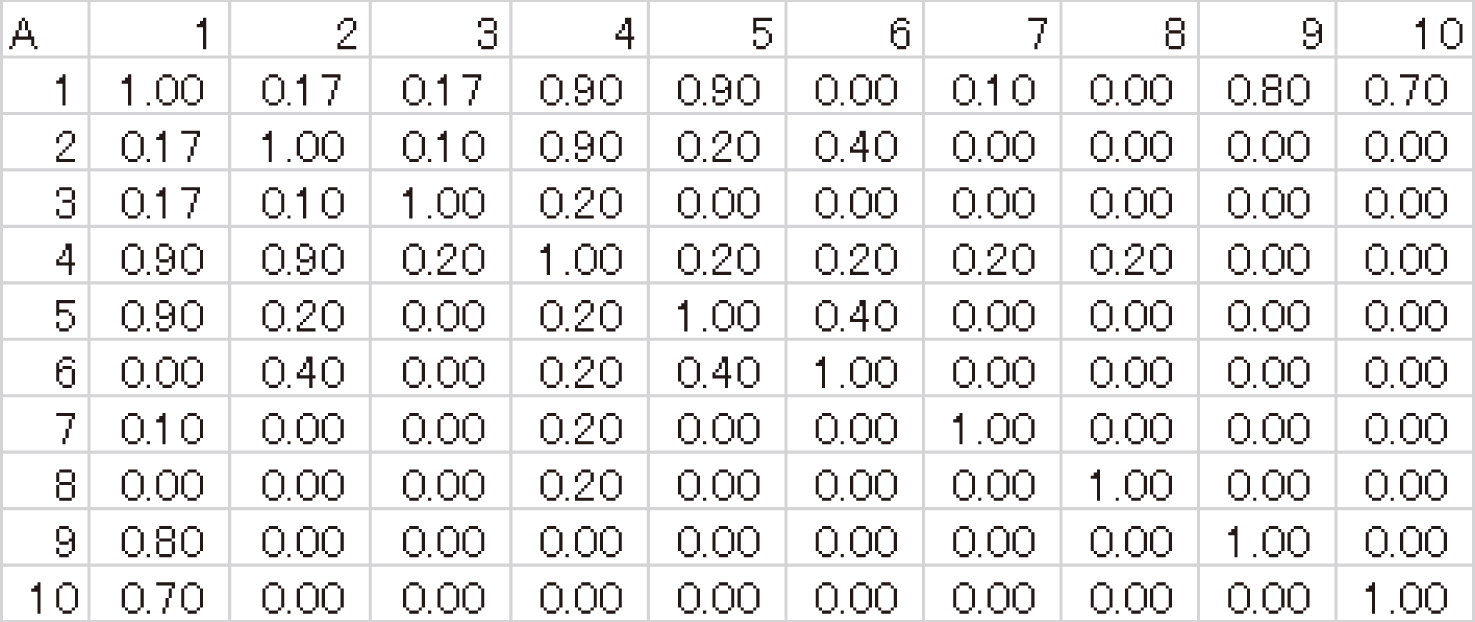
A, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 1, 1.00, 0.17, 0.17, 0.90, 0.90, 0.00, 0.10, 0.00, 0.80, 0.70 2, 0.17, 1.00, 0.10, 0.90, 0.20, 0.40, 0.00, 0.00, 0.00, 0.00 3, 0.17, 0.10, 1.00, 0.20, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00 4, 0.90, 0.90, 0.20, 1.00, 0.20, 0.20, 0.20, 0.20, 0.00, 0.00 5, 0.90, 0.20, 0.00, 0.20, 1.00, 0.40, 0.00, 0.00, 0.00, 0.00 6, 0.00, 0.40, 0.00, 0.20, 0.40, 1.00, 0.00, 0.00, 0.00, 0.00 7, 0.10, 0.00, 0.00, 0.20, 0.00, 0.00, 1.00, 0.00, 0.00, 0.00 8, 0.00, 0.00, 0.00, 0.20, 0.00, 0.00, 0.00, 1.00, 0.00, 0.00 9, 0.80, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00 10, 0.70, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 1.00
このモデルを実行すると以下のような解が得られます.
X, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 1, 1.00, 0.27, 0.15, 0.61, 0.65, 0.06, 0.10, 0.03, 0.57, 0.50 2, 0.27, 1.00, 0.10, 0.85, 0.15, 0.41, 0.00, 0.01,-0.04,-0.04 3, 0.15, 0.10, 1.00, 0.21, 0.01,-0.00,-0.00,-0.00, 0.01, 0.01 4, 0.61, 0.85, 0.21, 1.00, 0.34, 0.17, 0.20, 0.18, 0.12, 0.11 5, 0.65, 0.15, 0.01, 0.34, 1.00, 0.37,-0.00,-0.01, 0.10, 0.09 6, 0.06, 0.41,-0.00, 0.17, 0.37, 1.00, 0.00, 0.00,-0.02,-0.02 7, 0.10, 0.00,-0.00, 0.20,-0.00, 0.00, 1.00, 0.00,-0.00,-0.00 8, 0.03, 0.01,-0.00, 0.18,-0.01, 0.00, 0.00, 1.00,-0.01,-0.01 9, 0.57,-0.04, 0.01, 0.12, 0.10,-0.02,-0.00,-0.01, 1.00, 0.08 10, 0.50,-0.04, 0.01, 0.11, 0.09,-0.02,-0.00,-0.01, 0.08, 1.00
上に戻る