付属のモデリング言語 C++SIMPLE の使用により、線形計画問題、混合整数線形計画問題、二次計画問題、非線形計画問題をシームレスにモデリングし、求解する環境を提供します。
モデリング言語 C++SIMPLE を用いると数式に近い自然な形で問題記述ができるほか、自動微分機能により、大規模で複雑な非線形計画問題に対しても高階の微係数の情報を活かした精度の高いアルゴリズムを適用することが可能です。
また、概念上モデルとデータが分離されており、大規模問題を簡潔に記述することができます。
モデリング言語 C++SIMPLE は C++ のクラスライブラリとして実現されており、制御ループや出力などについては C++ 固有の機能を生かすことができるほか、他の C/C++ プログラムとのリンクも可能です。
以下で記述例をご紹介しておりますが、より詳しく知りたい方は Nuorium Optimizer C++SIMPLEマニュアル や Nuorium Optimizer C++SIMPLE例題集 をご覧ください。
モデリング言語 C++SIMPLE による問題の記述例
ナップサック問題(knapsack problem)
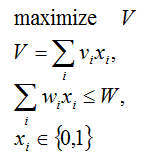
Set I;
Element i(set=I);
IntegerVariable x(index=i, type=binary);
Parameter v(index=i);
Parameter w(index=i);
Parameter W;
Objective V(type=maximize);
V = sum(v[i]*x[i], i);
sum(w[i]*x[i], i) <= W;平均・分散モデルによるポートフォリオの構成(portfolio problem)
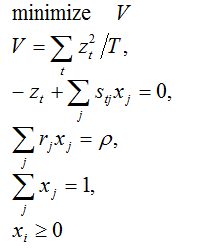
Set J;
Set Term;
Element j(set=J);
Element t(set=Term);
Variable z(index=t);
Variable x(index=j);
Parameter T;
Parameter s(index=(t,j));
Parameter r(index=j);
Parameter rho;
Objective V(type=minimize);
V = sum(pow(z[t], 2), t)/T ;
-z[t] + sum(s[t,j]*x[j], j) == 0;
sum(r[j]*x[j], j) == rho;
sum(x[j], j) == 1;
x[j] >= 0;ネットワーク最小コスト流問題(minimum cost flow problem)
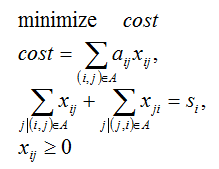
Set I;
Set A(dim=2, superSet=(I,I));
Element i(set=I);
Element j(set=I);
Variable x(index=A);
Parameter a(index=A);
Parameter s(index=i);
Objective cost(type=minimize);
cost=sum(a[i,j]*x[i,j], ((i,j), (i,j) < A));
sum(x[i,j], (j, (i,j) < A)) - sum(x[j,i], (j, (i,j) < A)) == s[i];
x[i,j] >= 0, (i,j) < A;一般非線形計画問題(Hock & Schittkowski No.25)
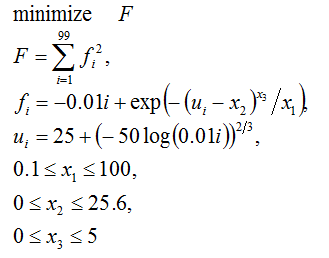
Set I="1 ... 99";
Element i(set=I);
Variable x1;
Variable x2;
Variable x3;
Expression u(index=i);
Expression f(index=i);
u[i]=25 + pow(-50*log(0.01*i), 2.0/3.0);
f[i]=-0.01*i + exp(-pow((u[i]-x2), x3)/x1);
Objective F(type=minimize);
F = sum(f[i]*f[i], i);
0.1 <= x1 <= 100;
0 <= x2 <= 25.6;
0 <= x3 <= 5;
x1 = 100;
x2 = 12.5;
x3 = 3;
