Nuorium Optimizer C++SIMPLE外部接続マニュアル V27

3.4 実行例

　さて，サンプルコードuseSolveQPの実行モジュールを作成して実行してみましょう．

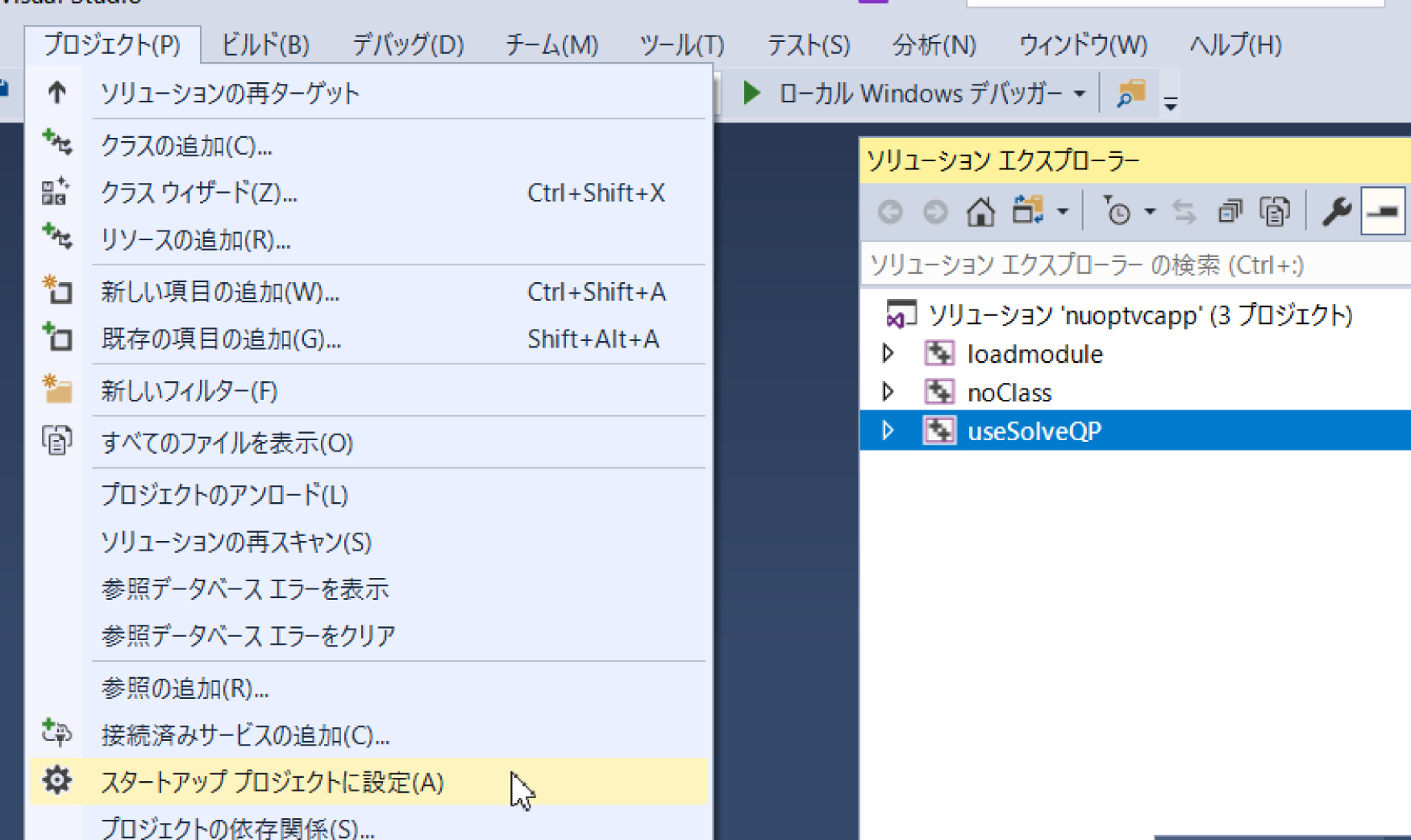
　プロジェクト「useSolveQP」を選択後，VC++のメニューの「プロジェクト」から「スタートアッププロジェクトに設定」を選び，プロジェクトを選択します．なおuseSolveQPの構成は「Release」に設定してあります．

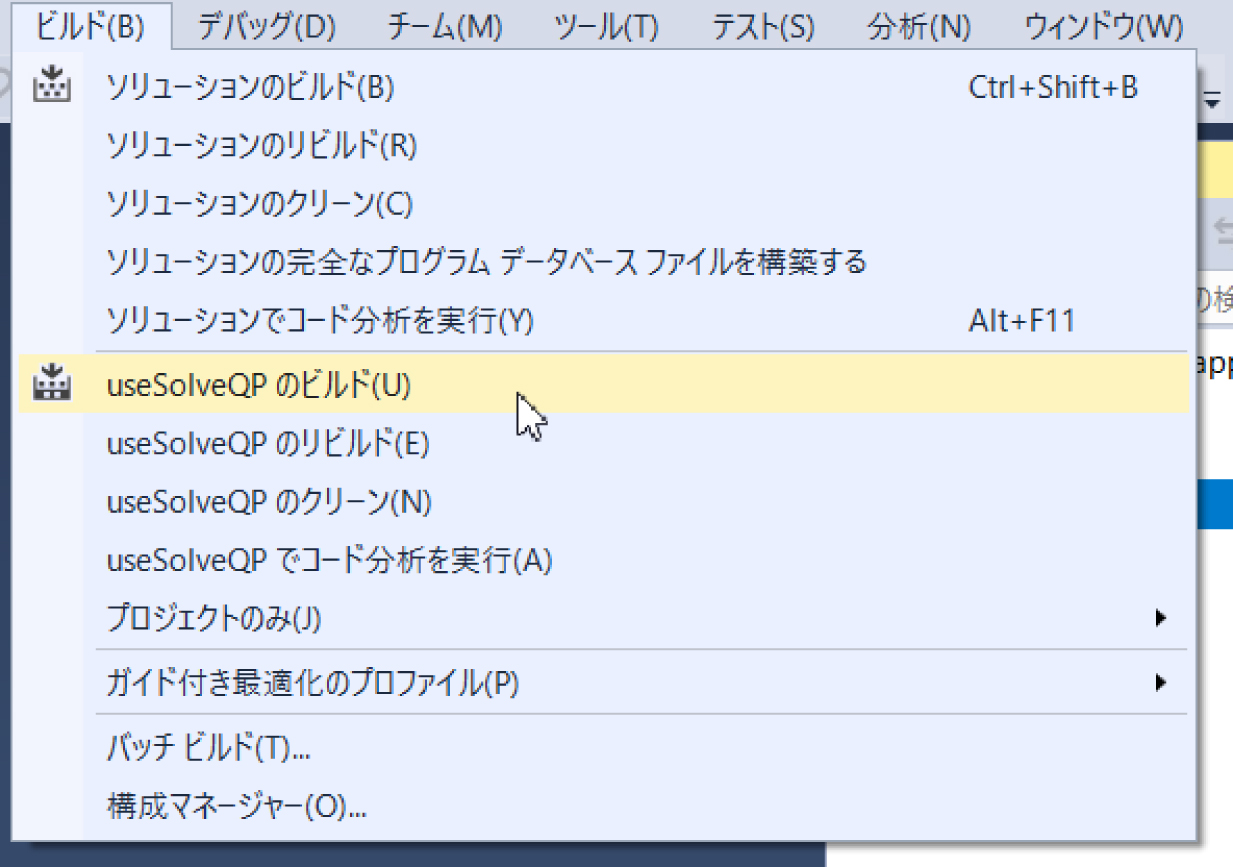
　続いて「ビルド」メニューから「useSolveQPのビルド」：

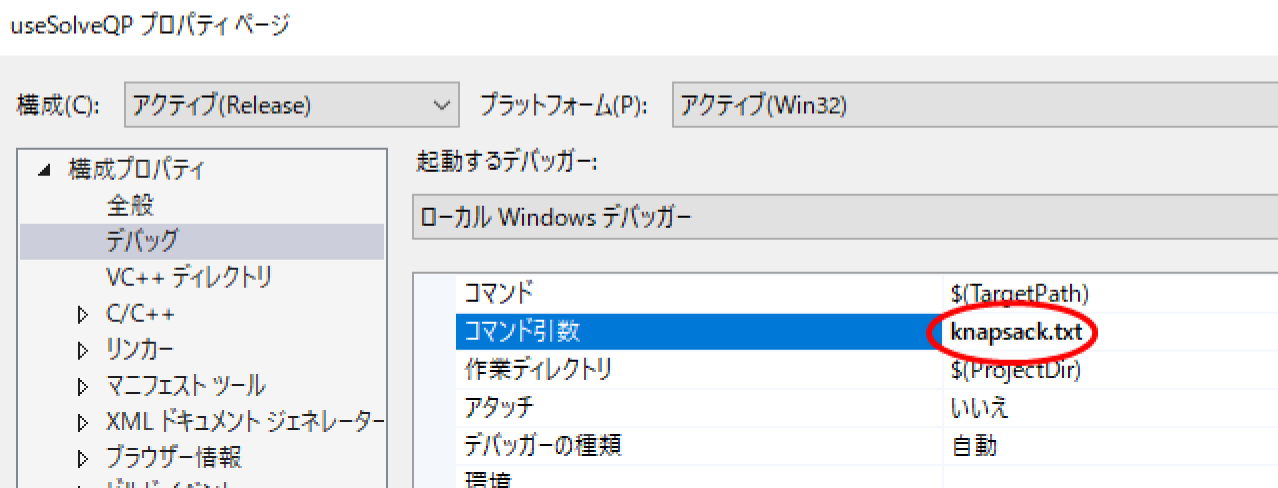
を選択するとuseSolveQP.cppがコンパイル，Nuorium Optimizerのライブラリとリンクされて，実行モジュールのuseSolveQP.exeが作成されます．引数としてknapsack.txtを与えるように「プロジェクト」→「プロパティ」→「構成プロパティ」→「デバッグ」の項目で，「コマンド引数」に「knapsack.txt」と入力します．

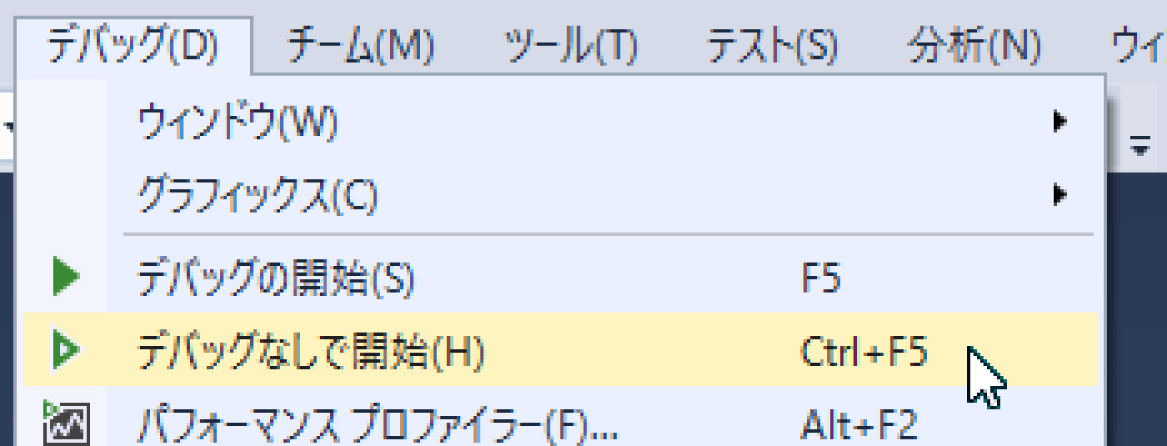
　つづいて「デバッグ」メニューから

と実行すると，実行経過表示ウィンドウが現れ，その中に以下のような出力が得られます．solveLPがコールされて出力が成されます．

[About Nuorium Optimizer]
Nuorium Optimizer x.x.x (NLP/LP/IP/SDP module)
         <with META-HEURISTICS engine "wcsp"/"rcpsp">
         <with Netlib BLAS>
, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.

[Problem and Algorithm]
PROBLEM_NAME                                          anon.LP
NUMBER_OF_VARIABLES                                        10
(#INTEGER/DISCRETE)                                        10
NUMBER_OF_FUNCTIONS                                         2
PROBLEM_TYPE                                     MAXIMIZATION
METHOD                                                SIMPLEX

[Progress]
<preprocess begin>.........<preprocess end>
<iteration begin>
Coefficient Statistics (after scaling)
  Coefficient range         [min,max] : [4.47e-01,3.04e+00]
  RHS and bounds            [min,max] : [1.00e+00,5.41e+00]
  Objective                 [min,max] : [5.67e-02,2.52e+00]

#sol         upper         lower   gap(%)  time(s)  list  mem(MiB)
#1          -1e+50            -0  100.000      0.0     0       10  sol: init

<<wcsp tabu search begin>>
  number of column singleton : 0
  number of column selection : 0
  Modify coefficients

<preprocess begin>..<preprocess end>
preprocessing time: 0.002(s)
<iteration begin>
--- TryCount = 1 ---
# random seed = 1
(hard/soft) penalty= 19/194, time= 0.00(s)
<greedyupdate begin>.........<greedyupdate end>
greedyupdate time= 0(s)
--- End Phase-I iteration ---
(hard/soft) penalty= 0/273, time= 0.00(s), iteration= 2
(hard/soft) penalty= 0/217, time= 0.00(s), iteration= 53
(hard/soft) penalty= 0/173, time= 0.00(s), iteration= 60
(hard/soft) penalty= 0/126, time= 0.00(s), iteration= 61
(hard/soft) penalty= 0/124, time= 0.01(s), iteration= 70
(hard/soft) penalty= 0/112, time= 0.01(s), iteration= 71
(hard/soft) penalty= 0/111, time= 0.01(s), iteration= 590
# (hard/soft) penalty= 0/111
# cpu time = 0.01/0.01(s)
# iteration = 590/1000
<iteration end>
# (hard/soft) = 0/111
# iteration = 1000
# time =  0.01 (s), succ = 1
<<wcsp tabu search end>>

#2          -1e+50           242  100.000      0.0     0       10  sol: wcsp

<iteration end>

[Result]
STATUS                                                OPTIMAL
VALUE_OF_OBJECTIVE                                        242
SIMPLEX_PIVOT_COUNT                                         0
PARTIAL_PROBLEM_COUNT                                       1
ELAPSED_TIME(sec.)                                       0.03
SOLUTION_FILE                                      solver.sol
optimalValue =  2.4200000000e+02
X:
[  1]  1.000e+00 [  2]  0.000e+00 [  3]  0.000e+00 [  4]  0.000e+00
[  5]  0.000e+00 [  6]  1.000e+00 [  7]  1.000e+00 [  8]  1.000e+00
[  9]  0.000e+00 [ 10]  1.000e+00
F:
[  1]  1.210e+02

C:\app\x64\Release\useSolveQP.exe (プロセス 17024) は、コード 0 を伴って終了しました。
このウィンドウを閉じるには、任意のキーを押してください . . .

　上に挙げた内容はNuorium Optimizerからの求解に関する出力です．問題の変数の数（NUMBER_OF_VARIABLES）や目的関数の値（VALUE_OF_OBJECTIVE）を知ることができます．Nuorium Optimizerの標準出力の内容については「Nuorium Optimizerマニュアル」（別冊）をご覧ください．

　

　Nuorium Optimizerの出力を抑制するには，

nuoptParam myParam; // 宣言

として，求解オプションを宣言したのち，

myParam.outputMode = "silent";

とします．また，デフォルトで出力されるNuorium Optimizerの求解レポートである解ファイルsolver.solの出力を抑制するには

myParam.outfilename = "_NULL_";

と設定し，solveQP()の最初の引数として渡します．useSolveQP.cppの以下のコメントを取ると，その設定になり，Nuorium Optimizerからの出力が抑制されて，useSolveQPが出力する表示のみになります．

       ..
       nuoptParam myParam;
    // Numerical Optimizerの出力と解ファイルの出力を抑制する．
    myParam.outputMode = "silent";
    myParam.outfilename = "_NULL_";
if ( nQelem || nQCelem ) { // 2次の係数があるのならsolveQP
     qpres = solveQP(&myParam
             ,n, m
     ..

　再びビルドメニューから

とすると，コンパイルが自動的に実行されます．

　

　knapsack.txtと同じ場所に別のuseSolveQP.cppの入力ファイル

useSolveQP\qp312.txt

があります．このデータは二次計画問題で

という定式で，次のように設定したものに対応します．2変数，3制約の問題で，制約式には二次の項はありません．

　VC++のGUIで「プロジェクト」→「設定」→「デバッグ」タブで，「プログラムの引数」を

qp312.txt

として再び実行してみてください．

　今度はuseSolveQPがsolveQPをコールして，次のような解が出力されます．

optimalValue = 2.3181818248e+000
X:
[  1] 9.394e-001 [  2] 1.212e-001
F:
[  1] -9.273e-001 [  2] -3.091e-001 [  3] 2.000e+000

　次のデータ：

（Nuorium Optimizerのインストール場所）\samples\appにあるzipファイルを解凍した中にあるuseSolveQP\qp312I.txt

はこの二次計画問題の変数を連続変数ではなく，整数変数という指定をつけたもので，二次の整数計画問題となります．これを入力として実行すると

optimalValue = 2.5000000000e+000
X:
[  1] 1.000e+000 [  2] 0.000e+000
F:
[  1] -1.000e+000 [  2] -2.000e-001 [  3] 2.000e+000

のような解が出力されます．

　さらに，次のデータ：

（Nuorium Optimizerのインストール場所）\samples\appにあるzipファイルを解凍した中にあるuseSolveQP\hs23.txt

は制約条件の中に二次式が含まれる問題となります．なお，このデータは[1]のNo.23を記述したものであり，次のような設定に対応します．

これを入力として実行すると

optimalValue = 2.0000000009e+000
X:
[  1] 1.000e+000 [  2] 1.000e+000
F:
[  1] 2.000e+000 [  2] 2.000e+000 [  3] 1.000e+001 [  4] 2.133e-010
[  5] 2.133e-010

のような解が出力されます．

---

 

 

上に戻る