PySIMPLE は Nuorium Optimizer の Python インタフェースです。 モデリング言語 C++SIMPLE の文法をできるだけ Python 環境に取り入れることにより、Python 環境でも数式に近い自然な形で問題記述ができます。
PySIMPLE では Nuorium Optimizer の求解ライブラリのうち(混合整数)線形計画問題、凸(混合整数)二次計画問題、二次制約付き二次計画問題、および制約充足問題に対しての接続インターフェースを提供します。他の問題クラスに対しては C++SIMPLE や RSIMPLE をご利用ください。
PySIMPLE は Python のパッケージとして実装されており、Python 固有の機能を活かすことができるほか、C++SIMPLE にはない特有の機能もございます。 以下で記述例をご紹介しておりますが、より詳しく知りたい方は Nuorium Optimizer/PySIMPLEマニュアル や 使ってみよう PySIMPLE バックナンバー をご覧ください。
PySIMPLE による問題の記述例
ナップサック問題(knapsack problem)
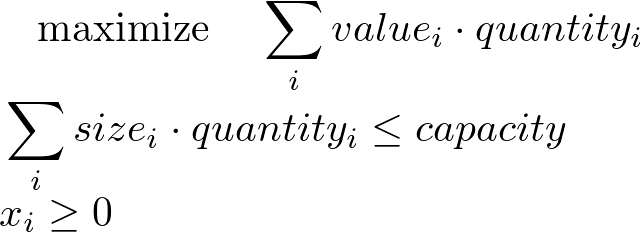
# -*- coding: utf-8 -*-
from pysimple import *
i = Element(value=...) # 品物
capacity = Parameter(value=.., name='ナップサックの容量')
value = Parameter(index=i, value=..., name='品物の価値')
size = Parameter(index=i, value=..., name='品物のサイズ')
quantity = IntegerVariable(index=i, lb=0, name='詰め込む個数')
problem = Problem(name='ナップサック問題', type=max)
problem += Sum(value[i]*quantity[i]), '総価値'
problem += Sum(size[i]*quantity[i]) <= capacity, '容量制約'
数独(sudoku)
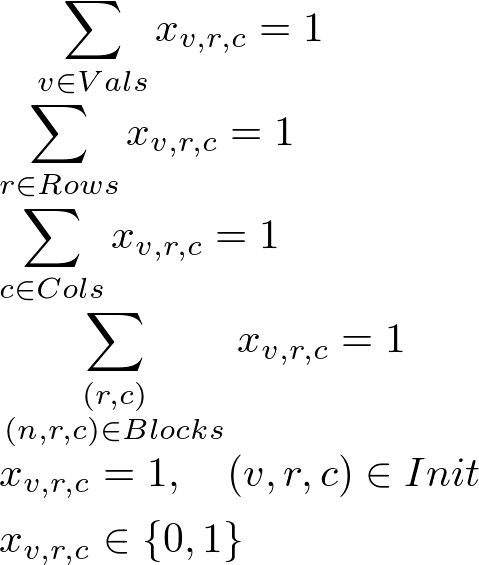
# -*- coding: utf-8 -*-
from pysimple import *
Vals = Rows = Cols = Set(value=range(1, 10))
v = Element(set=Vals)
r = Element(set=Rows)
c = Element(set=Cols)
Blocks = Set(value=[(s+1, s//3*3+t//3+1, s%3*3+t%3+1) for s in range(9) for t in range(9)])
b = Element(set=Blocks) # b(0) は Block 番号
init = Element(value=...) # 初期配置
x = BinaryVariable(index=(v,r,c)) # 値 v が (r,c) に入るか
prob = Problem(name='数独')
prob += Sum(x[v,r,c], v) == 1 # 各マスにはいずれかの値
prob += Sum(x[v,r,c], r) == 1 # 各値は各列のいずれか
prob += Sum(x[v,r,c], c) == 1 # 各値は各行のいずれか
prob += Sum(x[v,b(1,2)], b(1,2)) == 1 # 各値は各ブロックのいずれか
prob += x[init] == 1 # 初期条件
巡回セールスマン問題(traveling salesman problem)
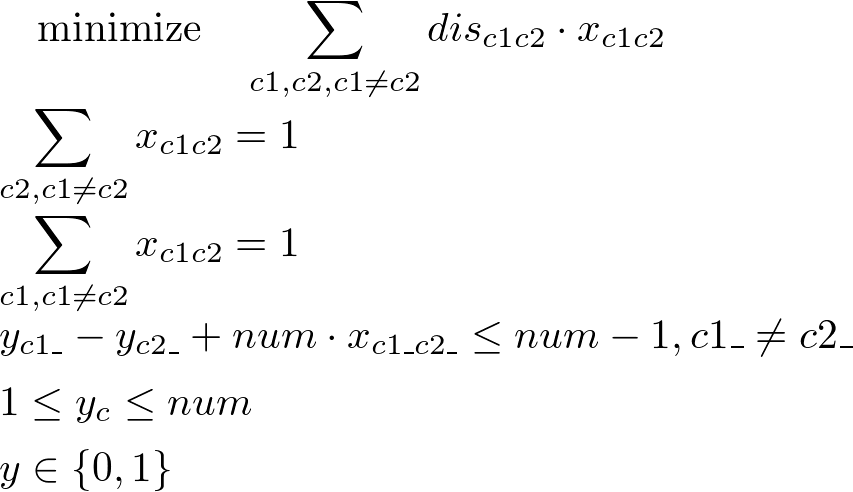
# -*- coding: utf-8 -*-
from pysimple import *
city = Element(value=...) # 都市
c1 = Element(set=city(0).set)
c2 = Element(set=city(0).set)
c_ = c1 != c1.set[0] # 出発地点を除く都市
c1_ = Element(set=c_.set)
c2_ = Element(set=c_.set)
dis = Parameter(index=(c1,c2), value=..., name='距離')
num = len(c_.set)
x = BinaryVariable(index=(c1,c2), name='移動')
y = Variable(index=c_, lb=1, ub=num, name='順番')
problem = Problem(name='巡回セールスマン問題', type=min)
c12 = c1!=c2
problem += Sum(x[c12]*dis[c12]), '経路長'
problem += Sum(x[c12], c12(1)) == 1, '各都市から1つの別都市へ'
problem += Sum(x[c12], c12(0)) == 1, '各都市に1つの別都市から'
c12_ = c1_!=c2_
problem += y[c12_(0)] - y[c12_(1)] + num*x[c12_] <= num-1, 'サブツアーを排除'
