主成分分析
主成分分析の目的
主成分分析とは、相関行列もしくは分散共分散行列を利用し、 複数の変数を統合して、データ全体の傾向・特徴を表す新たな変数を生成する方法である。 次元圧縮の手法の最も古典的な手法であることが知られている。
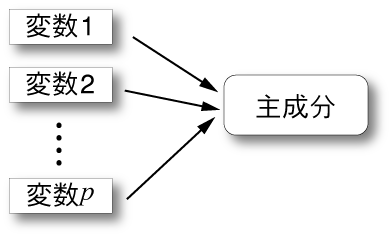
主成分分析の目的について理解するために、スポーツテストについて考える。ある学校では、反復横とび、立ち幅跳び、
ハンドボール投げなどをスポーツテストの種目として実施している。
もし、スポーツテストの結果から " 総合的に " 運動能力の高い人を表す指標
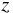 を作るには どうしたらよいだろうか、という問題があったとしたら、
どのような手法が妥当だろうか?
を作るには どうしたらよいだろうか、という問題があったとしたら、
どのような手法が妥当だろうか?
一つの考え方として、次のようなものがある。
ある競技者 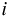 さん(ただし、
さん(ただし、 ) について、
競技
) について、
競技 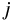 (ただし、
(ただし、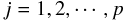 ) の記録が取れているものとすると、
) の記録が取れているものとすると、
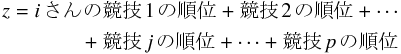
確かに、指標
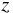 が小さいほど運動能力は良いといえるだろう。 しかし一つ問題がある。 例えば、競技 1 における 1 位と 2 位の差がほんのわずかで、
競技 2 における 1 位と 2 位の差が、競技 1 との差と比べてはるかに大きかったらどうだろうか?
つまり、どんなに記録に差があっても、それは全く考慮されずに順位の差という値で同じ扱いになってしまうのである。
が小さいほど運動能力は良いといえるだろう。 しかし一つ問題がある。 例えば、競技 1 における 1 位と 2 位の差がほんのわずかで、
競技 2 における 1 位と 2 位の差が、競技 1 との差と比べてはるかに大きかったらどうだろうか?
つまり、どんなに記録に差があっても、それは全く考慮されずに順位の差という値で同じ扱いになってしまうのである。
では、主成分分析ではどのように定めるのだろうか? 競技者 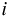 さんの、
ある競技
さんの、
ある競技 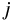 の記録を
の記録を  とし、
とし、
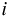 さんの運動能力を表す指標を
さんの運動能力を表す指標を 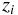 とすれば、主成分分析における
とすれば、主成分分析における
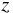 は、次のように表される。
は、次のように表される。
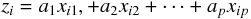
ここで、
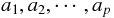 は定数である。 さて、どのようにしてこの係数を定めるのだろうか?
は定数である。 さて、どのようにしてこの係数を定めるのだろうか?
主成分分析の計算方法概要
話を分かりやすくするために、競技 A と競技 B の 2 種目に限って話を進める。 競技 A と競技 B の記録が得られたとして、散布図を描いてみると次のようになる。 ここで縦軸、横軸は、それぞれ競技 A、B の記録を表しており、 軸の方向に進むほど良い記録であることを示す。
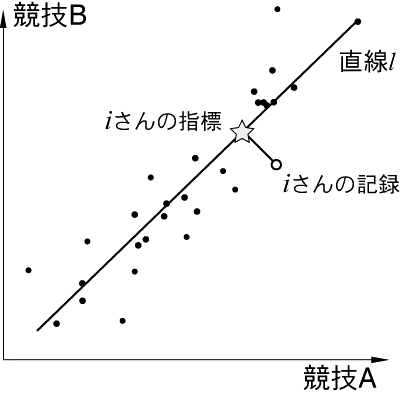
図1
この図を見ると、直線 l の右斜め上に行くほど成績が良いとしてもよさそうである。
仮に  さんの成績が ○ で表現されているとする。
このとき、主成分分析では、
さんの成績が ○ で表現されているとする。
このとき、主成分分析では、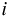 さんの運動能力を表す指標は、
元データの点から 直線 l に向けて垂線を下ろし、交わった点 ☆ である。
さんの運動能力を表す指標は、
元データの点から 直線 l に向けて垂線を下ろし、交わった点 ☆ である。
主成分分析では、データの相関を利用して直線 l を定めることができる。つまり、係数を定めることができる。この係数を「固有ベクトル」と呼ぶ。
主成分分析では、n 変数に対して、固有ベクトルを n 通り求めることが出来る。 図 1 を見ると、各データを直線 l 上の点で表現するとすれば、 垂線が持っている分の情報を失ってしまうことが分かる。そこで、垂線方向にもう一つ直線 l' を考える。 直線 l' に元データの点から垂線を下ろした直線 l' 上の点は、直線 l から元データの点までどれくらい離れているかという情報を持つことになる。 二つの直線 l と l' を使うことで、元データが持つ情報量を余すところなく表現できるのである。 データの変数が 2 つの場合、直線は 2 つ、つまり固有ベクトルは 2 つ求めることが出来るが、変数がn個の場合、同様の議論で固有ベクトルを n 個求めることができる。 通常、データ全体が持つ情報量のうち、一番情報が大きい成分を第 1 主成分と呼ぶ。同様に、情報量を持っている順番に、第 2 主成分、第 3 主成分、...と続く。
主成分分析の流れ
主成分分析の流れについて大まかな流れは、次のようになる。各ステップの解説は後述する。
- 分析の目的を定め、データを用意する
- 固有ベクトル、寄与率、主成分 ( 主成分得点 ) を求める
- 結果から主成分の解釈を行う
Visual R Platform による主成分分析の実行
ここでは、統計解析ツール Visual R Platform を使いながら、上記の手順を説明する。
- 分析の目的を定め、データを用意する
以下の表は車をいくつかの観点から評価し数値化したものである。これを用いて主成分分析を行う。
(データは「 こちら (cardata.csv) 」からダウンロード可能です) 。
| No. | 価格 | 燃費 | 車体重量 | 排気量 | 馬力 | 耐用年数 |
| 1 | 8895 | 33 | 2560 | 97 | 113 | 12 |
| 2 | 7402 | 33 | 2345 | 114 | 90 | 8 |
| 3 | 6319 | 37 | 1845 | 81 | 63 | 12 |
| 4 | 6635 | 32 | 2260 | 91 | 92 | 13 |
| 5 | 6599 | 32 | 2440 | 113 | 103 | 13 |
| 6 | 8672 | 26 | 2285 | 97 | 82 | 12 |
| 7 | 7399 | 33 | 2275 | 97 | 90 | 13 |
| 8 | 7254 | 28 | 2350 | 98 | 74 | 8 |
| 9 | 9599 | 25 | 2295 | 109 | 90 | 13 |
| 10 | 8748 | 29 | 2390 | 97 | 102 | 13 |
価格は単位$、燃費の単位はガソリン 1 リットルで進める距離 (km) 、車体重量は単位 kg、排気量は単位 cc、耐用年数は今後使用できると予想される年数である。
主成分分析により、様々な車の傾向を知りたい。たとえば 2 変数の関係であれば、散布図を書くことにより、線形の関係があるか? その関係から逸脱している車はないか? といったことが理解できるが、 このデータには 6 個の変数があるため、その関係を理解するには主成分分析が適当な手法である。
データを VRP にインポートし、利用可能にする。 データはファイルを VRP のプロジェクトボード (緑色の部分) にドラッグアンドドロップすることで、読み込みの準備が可能になる。
読み込みするファイルをプロジェクトボードにドラッグアンドドロップ (マウスボタンを押したまま移動) する。
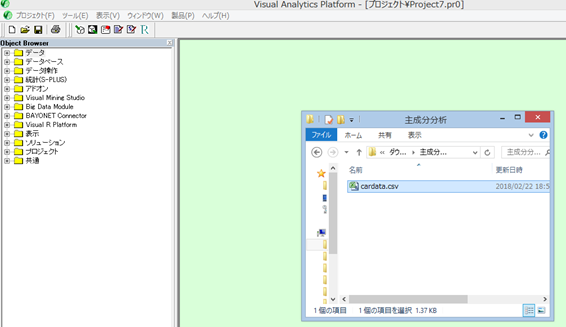
次のような小さいダイアログが表示されたら、「Rdataに変換」を選択する。
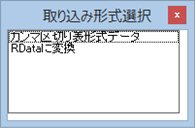
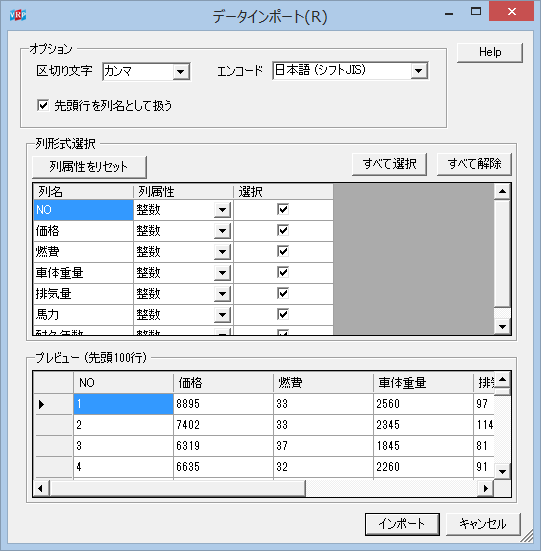
【cardata】アイコンをダブルクリックすると、データインポートのためのオプションを設定する画面が開く。 このデータでは特に変更する必要がなく、そのまま「インポート」ボタンをクリックするとデータ読み込みが完了する。
指定したcsvファイルはRデータにインポートされる。以降はこのデータを用いて、主成分分析を行う。
主成分分析をする
続いて、左側の【オブジェクトブラウザ】から、【Visual R Platform】フォルダをダブルクリックし、さらに【多変量解析】をダブルクリックする。 【主成分分析】アイコンをドラッグし、緑色のプロジェクトボードに移動させる
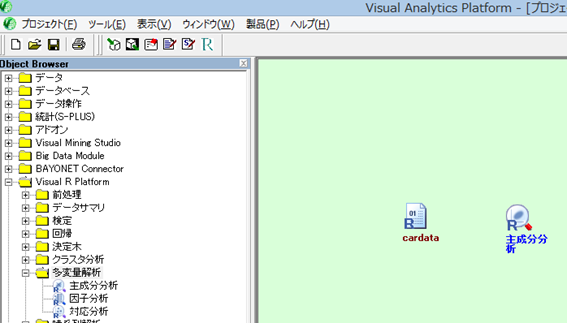
VRP では、矢印を引くことで、データの処理の流れを定義することができる。矢印は
- cardataアイコン上で右ボタンをクリックし、そのまま手を離さずマウスを移動させると線が表示される
- その線を【主成分分析】アイコンまで伸ばし、手を放す
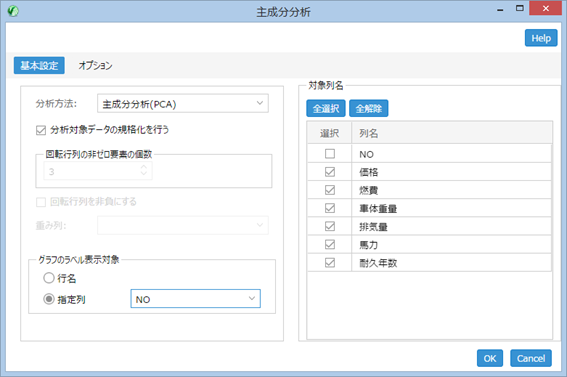
続いて、主成分分析アイコンをダブルクリックし、必要なオプションを設定する。
ここでは
- 対象列名:車の番号を表す NO 以外を選択
- 分析対象データの規格化を行う:チェック (デフォルト)
- グラフのラベル表示対象:指定列とし、列名から、【NO】を選択
- OK をクリック
「分析対象データの規格化を行う」オプションにチェックが入っていると、データの列ごとに、「平均 0、標準偏差 1」の線形変換を行い、主成分分析に当てはめる。 列ごとにデータの単位が異なる場合、値範囲が大きく異なる場合にはチェックをすることが望ましい。 また、「グラフのラベル表示対象」で選ばれた列は主成分分析の結果をグラフに表した際に、判別をするために使われる。
主成分分析の結果を考察する
※最新版の Visual R Platform 1.5 には、右ボタンクリックメニューでデータビューを選んだ時のビュアーに
- データ&グラフビュー (以前からあるバージョン)
- データ可視化 ( VRP1.5からビュアーとして利用可能なバージョン)
の 2 種類があります。この選択はメニュー「ツール / プロパティ」を選択、「表示」タブをクリックしたときの「可視化エンジン」から可能です。
V2.0 : データ&グラフビュー
V3.0 : データ可視化
「データ可視化」の方がグラフの種類数が多い、カスタマイズが可能等のメリットがありますが、 主成分分析の結果を見るには、「データ&グラフビュー」の方が見やすいので、ここでは「データ&グラフビュー」に切り替えて説明します。
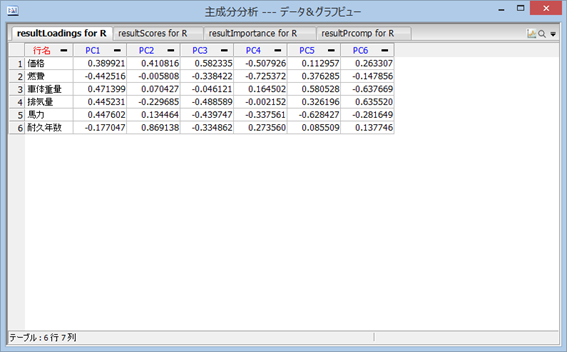
PC ( Principal Component ) とは、主成分を意味する。PC1 は第 1 主成分を表し、PC 2 は第 2 主成分を表す。
まずは、「resultLoadings」を選択し、確認する。これは、先に説明した「固有ベクトル」で、 内容は列ごとに見るが、PC 1 の列に現れた 6 個の値は、第 1 主成分の、 各変数 (価格、燃料、車体重量、排気量、馬力、耐久年数) に対する【固有ベクトル】の大きさを表す。 第 1 主成分の固有ベクトルの特徴を以下に示す。また、固有ベクトルは特に【因子負荷量 (loadings) 】とも呼ばれる。
- 耐久年数以外に対応する第 1 主成分 (PC1) の絶対値が大きい
- 価格・車体重量・排気量・馬力に対応する第 1 主成分 (PC1) の要素は正の値なので、これら変数の値が大きくなるにつれて第1主成分の値が大きくなる
- 燃費に対応する第 1 主成分 (PC1) の要素は、負の値なので、燃費が良くなると第 1 主成分の値は小さくなる
以上を考慮すると、第 1 主成分は『燃費が悪い車体や排気量の大きな車』であることを表す尺度であると解釈できる。
第 2 主成分 (PC2) は固有ベクトルを見ると、耐久年数に対応する固有ベクトルのみがかなり大きな値になっている。第 2 主成分 (PC2) は『長持ちする』ことを表す尺度である。
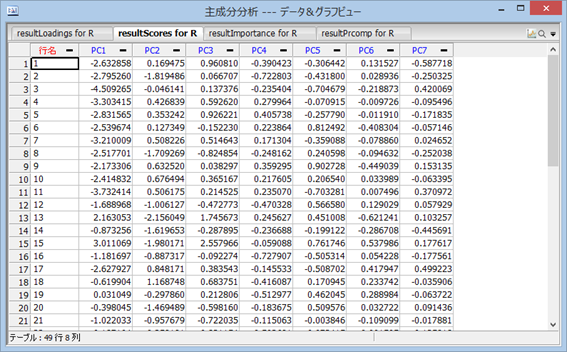
続いて、resultScores を確認する。これは固有ベクトル (因子負荷量) を使って計算された因子得点である。 PC 1 は第 1 主成分得点、PC 2 は第 2 主成分得点、と順に、この場合は第 6 主成分までが計算される。元のデータの順に計算され、保存される。
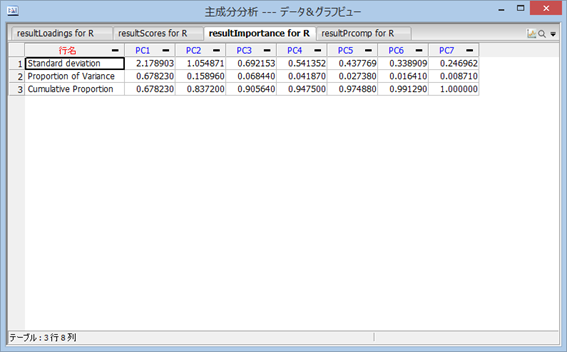
次に、resultImportance は、主成分分析の上から順に「標準偏差、寄与率、累積寄与率」を示している。 標準偏差はその主成分得点の変動がどれぐらい大きいかを示し、寄与率はそれがデータ全体の変動のうち、どの程度を示しているかの割合を表す。 累積寄与率は寄与率を第 1 主成分から順に足したもので、ここでは、第 6 主成分まであるので、第 6 主成分の累積寄与率は 1 になる。 この分析では、6 個の変数があるデータに対して、第 1 主成分と第 2 主成分の 2 列を使って、データ変動の 83.7% は表現可能であるということを言っている。 主成分分析は次元圧縮の手法の1つとして、広く知られている。
主成分分析の結果アイコンを右ボタンクリック、メニューから「オブジェクトビュー」を選択すると、その分析の解釈を助けるグラフが表示される (※)
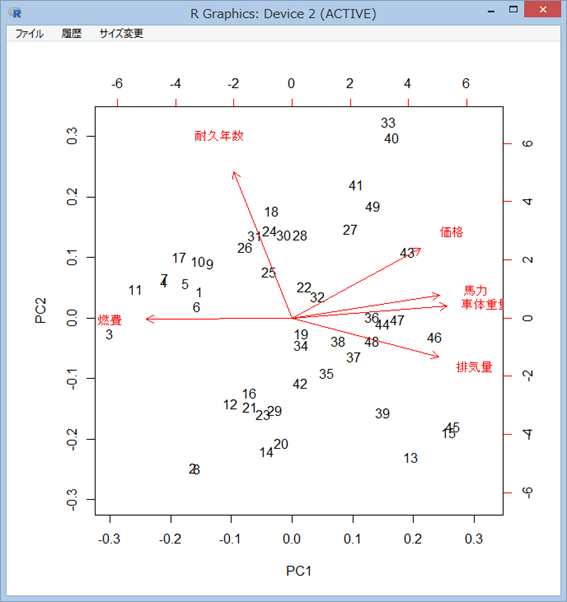
※)「オブジェクトビュー」がない分析もあります。
オブジェクトビューのグラフを見ると、2、8 番の車は、第1、2 主成分の得点がともに小さいので、 『燃費が良く車体の小さい、長持ちしない車』であることがわかる。 また、33、40、41、49 番の車は、第 1、2 主成分の得点が共に大きいので、『燃費の悪い大型車で長持ちする車』であることがわかる。13、15、39、45 番は第 1 主成分の得点が大きく、 第 2 主成分の得点が小さい。燃費が悪く車体が大きな、長持ちしない車であると言える。
主成分分析はこのように、n 次元のデータ (変数が n 個ある) を特徴を抽出して観察したいときに有効な手法である。
Visual R Platform による主成分分析について、さらに詳しく知りたいという方は 「統計解析ツール体験セミナー」にお申し込みください。 (セミナーのお申し込みは こちら から)


