線形回帰
1. 線形回帰の目的
線形回帰とは、変数間の相関を利用し、1 つあるいは、複数の変数の値を用いて、目的の変数の値を予測する分析である。 以降、予測するために用いる変数を説明変数、予測する変数を目的変数と呼ぶ。
2. 線形回帰
説明変数が 1 つの線形回帰を特に単回帰と呼ぶ。
2.1 単回帰の概要
次のようなシチュエーションを考える。ある、酒屋で主人は、その日の気温によって、ビールの売れ行きに違いがあることに気がついた。
そこで、ビールの販売ケース数と最高気温のデータを 5 日分取ってみた。酒屋のオーナーはこのデータを用いて、
今後の販売計画を立てられないかを考えたとする。
次に示すのが、酒屋のオーナーが収集した、ビールの販売ケース数と最高気温のデータである。
(データが欲しい方は「 こちら (beerdata.csv) 」からどうぞ)
| No. | 最高気温 (℃) | 販売ケース数 (ケース) |
| 1 | 18 | 24 |
| 2 | 20 | 27 |
| 3 | 22 | 29 |
| 4 | 25 | 30 |
| 5 | 28 | 36 |
表から関係は読取りにくいので、散布図を作成してみる。
図 2-1. beerdata の散布図
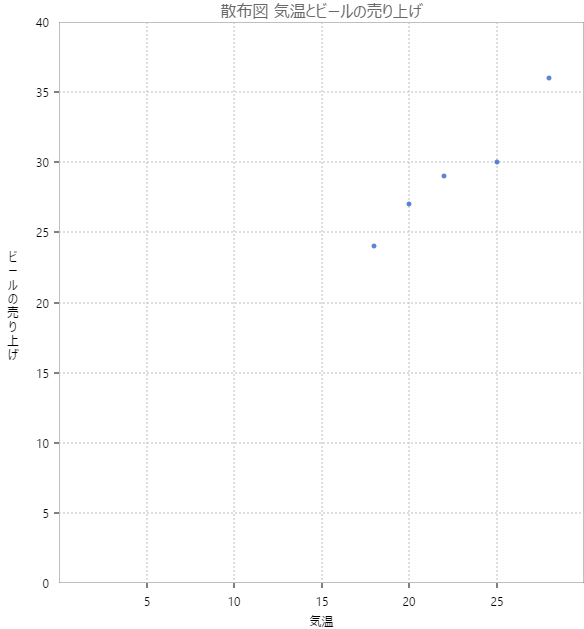
図 2-1 を見てみると、どうやら最高気温と販売ケース数の間には強い正の相関があるように見える。実際に相関係数を計算してみると、
相関係数は 0.97 でやはりかなり強い正の相関があった。正の相関が強いということは、片方の変数が増加 (減少) すれば、
もう一方の変数も増加 (減少) する関係があるということである。このような相関を利用して、
一方の変数からもう一方の変数を予測するのが単回帰である。
この相関関係に着目した酒屋のオーナーは、最高気温を説明変数として、ビールの販売ケース数を目的変数とする、単回帰をすることとした。
2.2 回帰直線と残差
単回帰は具体的にどのように行うかといえば、単回帰モデルというものを想定して、単回帰モデルに基づいて、分析を進めていくのである。
単回帰モデルについて説明する前に、用語と記号を確認しておく。なお以降、単回帰モデルのことを単にモデルと表現する。
まず、説明変数を 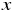 、目的変数を
、目的変数を 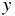 とおく。
また目的変数を予測した値は ^ をつけて
とおく。
また目的変数を予測した値は ^ をつけて 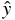 と表現する。
と表現する。
このように記号を定義したうえで、説明変数によって目的変数を説明するモデル式を次のように定義する。
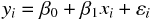
ここで 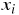 、
、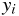 、
、
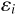 はそれぞれ、
はそれぞれ、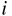 番目のデータの説明変数、
目的変数、誤差である。また
番目のデータの説明変数、
目的変数、誤差である。また 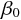 は定数項、
は定数項、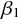 は係数である。
このモデル式は、目的変数が、定数項に係数と説明変数を掛け合わせたものを足した部分と、誤差で表現できることを示している。
は係数である。
このモデル式は、目的変数が、定数項に係数と説明変数を掛け合わせたものを足した部分と、誤差で表現できることを示している。
では、目的変数を説明変数のみを用いて予測するには、どうしたらよいか。
そのためには、目的変数と目的変数の予測値の差の合計ができるだけ小さくなるように、定数項と係数を推定したもの
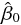 と
と 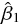 を用いて、モデル式において誤差を除いた次の部分に着目する。
を用いて、モデル式において誤差を除いた次の部分に着目する。
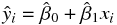
この式を回帰式と呼ぶ。この式は直線を示しており、回帰式によって引かれた直線を回帰直線と呼ぶ。
回帰式を用いるには、定数項の値と係数を推定すればよいことになる。では、この 2 つの値を求めるにはどうすればよいだろうか。
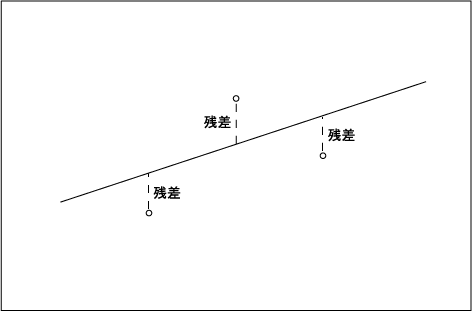
そのためには残差という考え方を導入する。残差は目的変数の実測値と予測値の差として次のように計算できる。
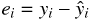
残差をわかりやすくするために図 2-2-1 のような例を考える。
図 2-2-1. 単回帰の例

この 3 点を最もよく説明する回帰直線は、下の 2 点を通ると仮定して、図 2-2-2 のような回帰直線を引いたとする。 すると、この回帰直線は通っている 2 点を完璧に説明することができるが、直線上に乗っていない残りの 1 点はうまく説明できないことになる。 このうまく説明できなかった部分、つまり点と直線の垂直方向の距離が残差である。
図 2-2-2. 2 つの点を通る回帰直線
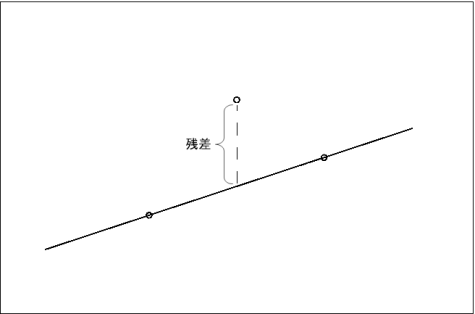
たとえば、回帰直線を 3 点の間を通るように上にシフトしてみると、今度はそれぞれの点に関して残差が生じるようになる。 この残差の大きさの合計が一番小さくなるような回帰直線が採用されることになる。ちなみに、回帰直線の傾きが回帰直線の係数、 切片が回帰直線の定数項ということになる。
図 2-2-3. 3 つの点の間を通る回帰直線
2.3 単回帰の最小 2 乗法を用いた回帰式の推定
最終的にすべての残差の大きさを合わせたとき最も小さいように回帰式を求めるのだが、その際には最小 2 乗法という考え方を用いる。
最小 2 乗法とは、残差平方和 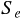 というものを最小化することを考える方法である。
残差平方和とはデータが n 個あるとき次のように計算される。
というものを最小化することを考える方法である。
残差平方和とはデータが n 個あるとき次のように計算される。
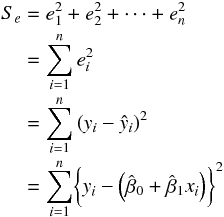
上記の式に実際にデータを入れて、残差平方和が最小になるような推定値 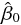 と
と 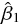 を
素直に計算することもできるが非常に煩雑である。そこで、2 つの推定値を偏微分という方法を用いて求めることを考える。
を
素直に計算することもできるが非常に煩雑である。そこで、2 つの推定値を偏微分という方法を用いて求めることを考える。
残差平方和を最小にするためには、推定したい係数 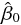 と
と 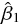 で
で 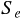 を
偏微分したものを 0 とおく。そうすると、
を
偏微分したものを 0 とおく。そうすると、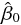 と
と 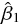 について次のような連立方程式が出来上がる。
について次のような連立方程式が出来上がる。
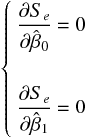
上の連立方程式に残差平方和を代入して整理すると次の連立方程式になる。
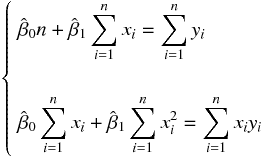
整理の前に平均、分散、共分散の定義を確認しておく。
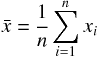
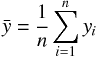
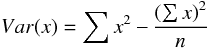
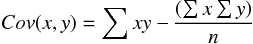
これらの定義を意識して、連立方程式を解くと 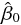 と
と 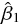 は、次のように解ける。
は、次のように解ける。
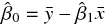
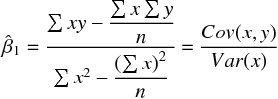
以上の手順で、先の酒屋のデータを用いて 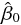 と
と 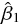 を推定すると、次の回帰式を得た。
を推定すると、次の回帰式を得た。
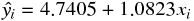
2.4 回帰式の評価
回帰式を用いて予測をする上で、回帰式がどの程度の予測精度を持つのかを把握するのは重要である。 いくつかの評価方法があるが、今回は次の方法を紹介する。
- 重相関係数から計算される寄与率 (決定係数)
- 平方和の比から計算される寄与率 (決定係数)
寄与率 (決定係数) 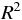 とは、0 から 1 の間をとり、その値が 1 に近いほど予測精度のよい回帰式であるといえる。
明確な定義があるわけではないが、予測精度の判定の目安を示す。
とは、0 から 1 の間をとり、その値が 1 に近いほど予測精度のよい回帰式であるといえる。
明確な定義があるわけではないが、予測精度の判定の目安を示す。
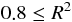 :精度がよい
:精度がよい
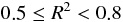 :まあまあ精度がよい
:まあまあ精度がよい
寄与率 (決定係数) は 2 通りの方法で求めることができる。
重相関係数 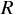 から計算される寄与率 (決定係数)
から計算される寄与率 (決定係数)
重相関係数とは、説明変数と説明変数の予測値の相関のことである。 この重相関係数の 2 乗が寄与率 (決定係数) である。酒屋の例は以下のとおりである。
| No. | 目的変数の実測値 | 目的変数の予測値 |
| 1 | 24 | 24.22152 |
| 2 | 27 | 26.38608 |
| 3 | 29 | 28.55063 |
| 4 | 30 | 31.79747 |
| 5 | 36 | 35.04430 |
ここから、重相関係数を求めると、

さらに、重相関係数を 2 乗して寄与率 (決定係数) を求める。
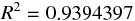
平方和の比から計算される寄与率 (決定係数)
まず、3 つの平方和を定義しておく。1 つ目に目的変数 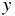 の変動の大きさを表す、
目的変数による平方和
の変動の大きさを表す、
目的変数による平方和 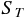 は、次の式で定義される。
は、次の式で定義される。
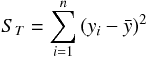
2 つ目に予測値 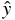 の変動の大きさを表す、
回帰による平方和
の変動の大きさを表す、
回帰による平方和 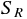 は、次の式で表現される。
は、次の式で表現される。
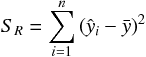
3 つ目に残差 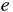 の変動の大きさを表す、
残差平方和
の変動の大きさを表す、
残差平方和 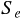 は次の式で表現される。
は次の式で表現される。
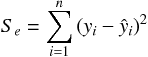
ここで酒屋のデータを用いて、3 つの平方和をそれぞれ計算してみる。
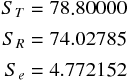
3 つの平方和には次の関係がある。
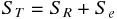
実際に酒屋のデータで計算してみると、3 つの平方和の関係が成立していることが確かめられる。この関係を図に示すと次の通りである。
図 2-4. 3 つの平方和の関係
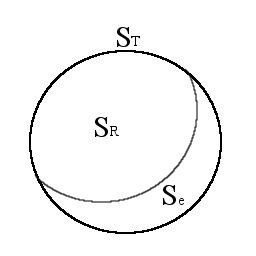
3 つの平方和の関係を考えてみると、目的変数による平方和のうち、どのくらい、回帰による平方和が占めているかが、 回帰式の予測精度の評価に使えそうである。実は、寄与率 (決定係数) は 3 つの平方和を用いて次のように計算できる。
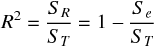
上式を用いて、寄与率 (決定係数) を計算した結果は、先に重相関係数の 2乗 から計算したものと等しくなる。
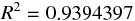
2.5 酒屋の話
以上の単回帰の結果、酒屋のオーナーは 1 ℃気温が上がるごとに、1 ケースビールが多く売れるという知見を得た。
酒屋のオーナーは、次の日の天気予報や、長期予報に敏感になり、気温が低いと予測される日には、ビールの安売りを打ち出して、
売り上げの減少を避け、気温が高いと予測される日には、ビールの売り場を入り口やレジ付近に近づけるなどし、ビールの売り上げ増加を図った。
また、夏季の平均気温が高いと予測されたら、入荷量を増やし、逆に平均気温が低いと予測されたら、入荷量を減らすなどした。
このように、線形回帰は用いられることがある。
3. Visual R Platform (VRP) を用いた線形回帰
3.1 線形回帰の設定
線形回帰の理論を説明し終えたところで、実際に Visual R Platform を用いて線形回帰をする方法を説明する。
この節では例として、年齢から年収を予測することを考える。この場合、予測したい変数である年収は目的関数、年齢から年収を予測するので、
年齢は説明変数となる。
次に示すのが、年齢と年収のデータ (一部) である。 このデータにはある仮想企業に勤める 100 人の年齢と年収のデータが含まれている。
(データはこちら (salarydata.csv) 」からダウンロード可能です)
| No. | 年齢 (才) | 年収 (万円) |
| 1 | 21 | 315 |
| 2 | 33 | 493 |
| 3 | 38 | 556 |
| 4 | 32 | 527 |
| 5 | 44 | 664 |
| 6 | 20 | 269 |
| 7 | 43 | 630 |
| 8 | 35 | 533 |
| 9 | 43 | 672 |
| 10 | 38 | 555 |
3.2 データを VRP にインポートし、利用可能にする
データはファイルを VRP のプロジェクトボード (緑色の部分) にドラッグアンドドロップすることで、読み込みの準備が可能になる。
読み込みするファイルをプロジェクトボードにドラッグアンドドロップ (マウスボタンを押したまま移動) する。

次のような小さいダイアログが表示されたら、「Rdata に変換」を選択する。
【salarydata】アイコンをダブルクリックすると、データインポートのためのオプションを設定する画面が開く。 このデータは特に変更することなくデータ読み込みが完了する。
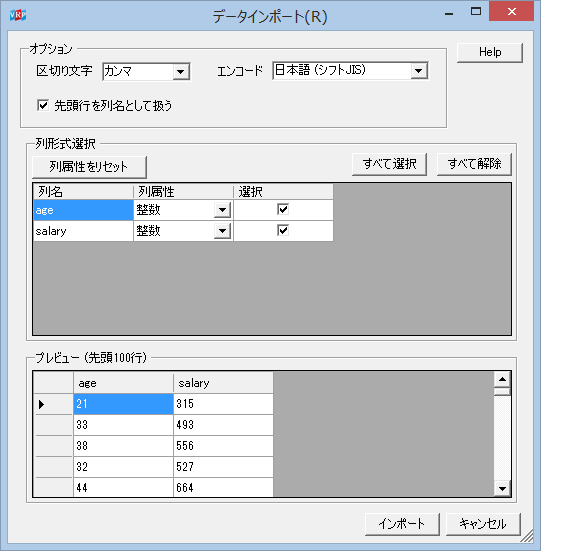
インポートボタンをクリックすると、csv ファイルは R データにインポートされる。以降はこのデータを用いて、線形回帰を行う。
3.3 線形回帰をする
続いて、左側の【オブジェクトブラウザ】から、【Visual R Platform】フォルダをダブルクリックし、さらに【線形回帰】をダブルクリックする。 【線形回帰】アイコンをドラッグし、緑色のプロジェクトボードに移動させる。

VRP では、矢印を引くことで、データの処理の順番を定義することができる。矢印は
- salarydata アイコン上で右ボタンをクリックし、そのまま手を離さずマウスを移動させると線が表示される
- その線を【線形回帰】アイコンまで伸ばし、手を離す
続いて、線形回帰アイコンをダブルクリックし、必要なオプションを設定する。
ここでは
- 目的変数から【salary】を選択
- 説明変数の【age】をチェック
- OK をクリック
する。重回帰を行う場合は、説明変数を複数選択する。
【線形回帰】アイコンの文字の色が赤になったら、結果がそのアイコンに保持されていることを示している。
3.4 線形回帰の結果を考察する
線形回帰アイコンを右クリックし、メニュー【データビュー / 開く】を選ぶと、結果をチェックすることができる。 結果は 4 つのタブで表示される。
保持されている結果は次の通り
- predict for R:各説明変数から、回帰式を用いて計算した結果 (salary.予測) と、 実際の値とのかい離 (残差)。残差は小さいほど当てはまりが良い。
- coefficients for R:切片 (Intercept) と説明変数に対する回帰係数、【estimate】が予測値で、
その標準誤差や t 値、回帰係数が 0 という帰無仮説に対する P 値が計算される。
P 値が十分に 0 に近いとその回帰係数が意味を持つことを示している。
結果では、切片も age に対する回帰係数も P 値が十分に小さいので、回帰式が意味を持つことを示している。
Coefficients から給料の線形回帰について、次の回帰式が得られた。
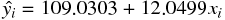
- evaluate for R:回帰式全体に対する統計量を示している。特に重要なのは決定係数 (寄与率) で、87.46 % である。 これはデータ変動の内、この回帰式を用いることにより、87.46 % を説明できるということを表している。(数式等は上記 2.4 回帰式の評価 を参照)
Visual R Platform による線形回帰について、さらに詳しく知りたいという方は「統計解析ツール体験セミナー」にお申し込みください。 (セミナーのお申し込みは こちらから)


