1. 割り当て問題と二部グラフ#
1.1. 背景#
割当問題とは 2 つの集合間の要素をどのように対応させるかを決定する問題である.
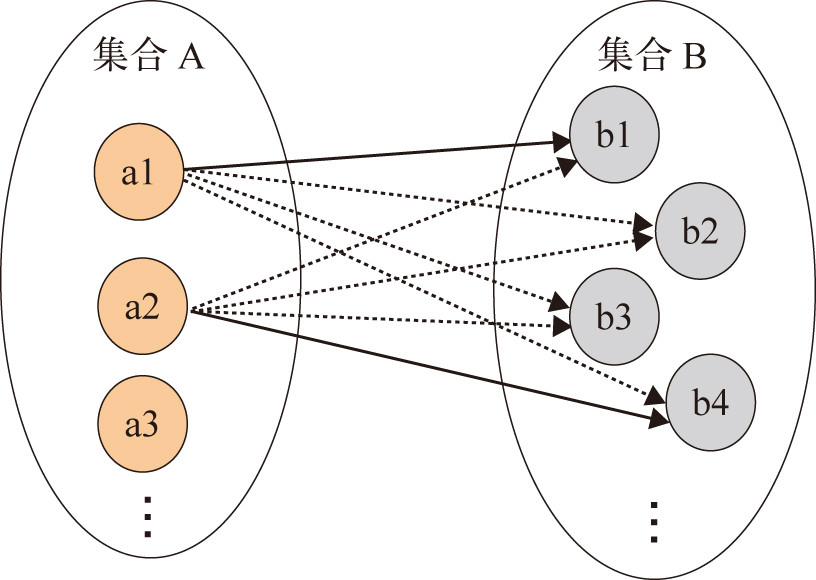
図 1.3 割り当て問題#
基本的な組合せ最適化問題でもあり,割当問題は応用範囲が極めて広い. この応用範囲の広さは問題自体のわかりやすさと,問題の変形の容易さが要因として大きいだろう.
割当問題もまたネットワークとしての側面を,二部グラフとして容易に見出すことができる. それ故に定式化の見通しがよく,次に挙げるように様々な具体的な問題設定として整理されている.
人員配置問題
シフトスケジューリング問題
配車計画問題
訪問スケジューリング決定問題
マーケットテリトリー決定問題
以上のように,数理最適化による定式化を考えるうえでは,ネットワークの概念一般だけでなく, 割り当て問題を背景に持つ二部グラフもそれ単体で個別に整理しておくことは重要である.
注釈
割当問題一般の場合には必ずしも二部グラフとして捉えることができないこともあるが, 二部グラフの範囲で扱うことができる問題は実務において決して少ないわけではない. むしろ典型的な問題でさえあるといってもよいだろう. ここでいう典型的とは,問題の核となる部分を二部グラフ, またはそれと同等のものとして捉えることができるということである. このような事情のため,二部グラフに限定して,割り当て問題を扱うものとする.
1.2. 割り当て問題と表形式データ#
抱えている実務問題に割当問題の構造を持っているかどうかは, 次の表形式のデータをもとにした作業が存在しているかどうかという視点を持ってみるとよい.
c1 |
c2 |
c3 |
c4 |
|
|---|---|---|---|---|
r1 |
||||
r2 |
||||
r3 |
||||
r4 |
この表は空であるが,どのような意味を与えることができるだろうか.
1.2.1. 対戦表#
例えば対戦表として解釈するならば,次のような表が書けるだろう.
1 |
2 |
3 |
4 |
|
|---|---|---|---|---|
1 |
/ |
x |
o |
x |
2 |
o |
/ |
o |
o |
3 |
x |
x |
/ |
x |
4 |
o |
x |
o |
/ |
この表データから対戦成績は次のとおりであったことが読み取れる.
1 は一勝二敗
2 は全勝
3 は全敗
4 は二勝一敗
このような対戦表を大規模に複数作成する中で, 実力が拮抗するように対戦参加者を組みたいと思ったとしよう. すると上記の例では 2 と 3 が同じ対戦表にいた組み合わせは,歓迎されない対戦表であった可能性が高い. そのようなことが起こらないように,対戦表を完成させることは, 人力では途端に難しい問題となることが予想できる.
1.2.2. スケジュール表#
次のような表を書けば,スケジュール表としても解釈できる.
1 |
2 |
3 |
4 |
... |
30 |
31 |
|
|---|---|---|---|---|---|---|---|
m1 |
A |
A |
R |
C |
... |
A |
A |
m2 |
A |
B |
R |
C |
... |
A |
R |
m3 |
A |
C |
R |
A |
... |
B |
R |
m4 |
B |
B |
R |
A |
... |
A |
R |
この表はある月の四名のスケジュール表であり, A, B, C, R は作業シフトの種類を表していると思われる.
このスケジュール表は人ではなく,機械の作業スケジュール表かもしれない. 表形式のデータは実に様々に解釈できる.
このようなスケジュールを作成するのは, 異なった複数の特性を持つ個が集団で統率をとることで, 個では達成できないより大きな事柄を行ったり, もしくはある一定の水準を維持したりといったことなどの用途のためにある.
スケジュール表の作成は個や作業内容の豊富さを考慮して作成する必要があり, こちらもまた人の手ですべての要求を満たすことは難しい問題である.
注釈
割当問題が難しいのは組み合わせの数が膨大になり, 総当たりで調べようとすると,とても現実的な時間では計算が終わらないこととして, 簡単に説明できる.
このこと自体は間違いではないが,効率的なアルゴリズムが存在しないことまでは述べていない. 我々は数理最適化の文脈で,現実的な計算時間で解を得ようとするものであるが, 一方で割り当て問題に特化した非常に効率が良いアルゴリズムもまた知られている.
このように聞くと,数理最適化でアプローチするのはなく, その効率が良いアルゴリズムで考えればよいのではないか,と思うかもしれない. これは確かに正しい主張ではあるものの, その効率が良いアルゴリズムは,解くべき問題を特定しており, 前提となる事柄が満たされないと,使用できないということがよくある.
実務要件は仮にシステムが完成しても,今後,仕様がどのように変化するかを予測できない怖さがある. ある問題に特化した専用のアルゴリズムでシステムが実装されていた場合には, そのような仕様変更に耐えられない可能性が高くなってしまうが, 数理最適化であれば,制約条件や目的関数の調整によって済む汎用性が,専用アルゴリズムと比較してあると期待できる. このような理由のために,数理最適化で解決ができないかをまずは模索することが肝要である.
1.3. 表形式データと二部グラフ#
対戦表やスケジュール表といった例を見たが, 表形式データとして整理される組み合わせは他にも様々なものがあり, ありふれているとさえ言ってもよいだろう.
表形式のデータの表現力は強く,また自由度も高いため, 整然データという概念もあるほどである. 加えて表計算ソフトがごく身近な存在であることも,表形式データの頻出性の証左であろう.
この表形式データは二部グラフへと自然に対応させることができ, 割り当て問題としての肥沃な土壌を与えている.
代表的な対応は行からなる集合 \(R\) と列からなる集合 \(C\) を考え, これらの間の割り当て問題を考えることである.
もしくはより一般に整然データとして整理して,列の数だけ集合を考えて, それら集合間の割り当て問題と考えてもよい.
例えばスケジュール表は人・日付・シフトの 3 つの集合 \(M\), \(D\), \(S\) を考えて, これら集合で作る三組 \(MDS\) のどの要素を選び出せばよいか,というように割り当て問題を捉えることもできる.
今述べたことは,変数の立て方を意図しており,制約条件や目的関数については言及していない. 割り当て問題としての構造が見えると,変数としては何になるかが自然と決まる. 後は問題ごとに様々な制約条件や目的関数を設定することとなり, このようして様々な割り当て問題が考えられることとなる.
注釈
実務で扱われている表形式データは往々にして整然データではない. 表計算ソフトで管理されている場合にはセル結合であったり,一つのセルが複数分割していたりして, 機械的に整然データへと整形できないこともある. また部署間でデータの形式が統一されていないことも珍しいことではない.
定式化の道筋が見えたとしても,データ整理の方に労力を費やすこととなるのは, 割り当て問題を扱う場合にはよくあることと思ってよいだろう.
引用書式
