3. 生産計画問題#
3.1. 背景#
生産計画問題とは工場の生産能力が定量化されており,またコントロール可能な場合に, どれだけ生産すれば所定の目的関数の意味 (コスト最小化や利益最大化等) で必要十分であるかを決める問題である.
生産計画問題と一口に言っても広義には, 生産管理の対象となる様々な計画に対する問題全般を意味するため, 定式化もまたその対象ごとに複数ある.
最適化項目についても力点を置きたい生産管理対象によって, 例えば以下のように様々な場合がある.
計画期間内での在庫量の最小化
納期の遵守
全体の計画期間の最小化
3.2. 設定#
注釈
本例題は数ある生産計画問題のうち,次の特徴をもった問題であることが重要である.
生産量のみに着目する.製品を生産する際の各工程の組み合わせやタイムスケジュールを問うものではない.
生産のための工場という拠点と,生産された製品を欲している需要地や生産余剰分を保管しておく倉庫といった拠点がある.
これらは生産計画問題の全般で共通するか,もしくは生産計画問題を数理最適化で扱う場合に, 線形定式化の観点で扱える基本的な問題設定になっている.
3.3. 集合#
与えられた設定には様々な事柄が言及されているが,そのうちで「集まり」と考えられる対象は次である.
- 原料の集まり
- (1)#\[m\in MATERIALS = \{A,B\}\]
- 製品の集まり
- (2)#\[p\in PRODUCTS = \{I,II\}\]
- 期間の集まり
- (3)#\[t\in TERMS = \{1,2,3\}\]
注意
「工場の集まり」を考えなかった. 単純に問題設定で記述されていなかったことが理由であり,実際,簡単のため,我々は一つの工場しか以下では考えない.
しかし実際の要件整理の中では工場が複数あることは, 時として暗黙の了解でありさえするので注意が必要である.
3.4. 変数#
決定すべき事柄は次である.ここで \(\mathbb{R}_{\geq 0}\) は非負実数集合である.
- 製品 \(p\) の期間 \(t\) に対する生産量
- (4)#\[x[p,t] \in \mathbb{R}_{\geq 0}\]
- 製品 \(p\) の期間 \(t\) に対する在庫量
- (5)#\[y[p,t] \in \mathbb{R}_{\geq 0}\]
Tip
単に「生産量」「在庫量」とだけ述べるのではなく, それらが先んじて定式化を図った集合の要素を用いて, どのように自然言語で述べることができるのかを整理することが望ましい.
要件整理や変更を検討する際に,定量化された議論が可能になるからである.
例えば変数の添字が増減することで,変数の数もまた増減するが, それがどのように変わりえるのか,そしてその変化はどの集合によるものが影響力が多いのか, といった事柄を定量的に議論できる.
生産量と在庫量との関係から出荷量を定義できる.
- 製品 \(p\) の期間 \(t\) に対する出荷量
- (6)#\[\begin{split}z[p,t] := \begin{cases} x[p,t] - y[p,t] & (t=1), \\ x[p,t] - y[p,t] + y[p,t-1] & (\mathrm{otherwith}) \end{cases}\end{split}\]
式で表記することと合わせて下図のように,数量関係のネットワークフロー図を表記しておくとよい.
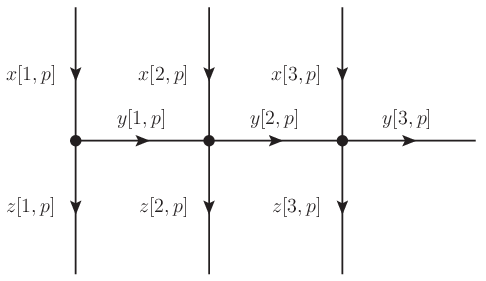
図 3.1 生産量・在庫量・出荷量の相互関係#
今の場合には図の辺には数量を割り当て,横軸には時間軸を意図している. 何かしらの順序構造があれば,ネットワークフローの描画にそれを反映させると見通しやすくなることが多い.
注釈
順序構造とは簡単に言えば,集合の要素間に大小関係が定められていることをいう. 時間的な集合はその代表例である.
例えば一年間の月数からなる集合があったとする.
一年が年度区切りであるならば,\(4\) が最も小さく,\(3\) が最も大きく,各月は次の順序になっている.
注釈
期間が関連する最適化では計画範囲外の期間との接続がしばしば問題となる.
3.5. 制約条件#
問題設定から次の守るべき規則 (制約) があると読み取れる.
製品 \(p\) は所定の原料を消費して一単位が生産される.
製品 \(p\) の期間 \(t\) の出荷量 \(z[p,t]\) は需要量以上でなければならない.
3.5.1. 原料制約#
各原料から製品を加工する方法については明示されていないが, 線形な定式化で表現するにはどうなるかを考えてみる.
線形な定式化を図るので変数である生産量に対して線形な式になっていなければならない. すると生産量の一単位当たりの数量が重要となる.
そこで次の定数を導入する.
- 製品 \(p\) を一単位生産するのに要する原料 \(m\) の消費量
- (9)#\[C[m,p]\]
これによって期間 \(t\) に消費する原料 \(m\) の総量は次で線形に定式化できる.
さて原料は各期間でどれだけの量を消費可能だろうか. 問題設定には陽に述べていないが,もし無尽蔵に消費できるとしたら, わざわざ原料にまで戻って数量関係を問う意味がなくなる. 単純に製品の生産量だけを議論すればよいことになる. 任意の生産量を仮定できるからだ.
しかし今は原料まで遡って言及しているので,消費可能な数量には各期間で上限値 \(U[m,t]\) があるものと推測できる. よって次の原料消費量に関する上限制約を考えることができる.
重要
原料制約の定式化からは次の二点を学ぶことができる.
線形な定式化を前提とするため,一単位当たりの数量係数は何かを常に問題設定から読み取ると,自然に定式化すべき変数や定数および式が立式できるようになる.
より内部の規則に還元される場合には何かしらの上限値 (場合によっては下限値) が設定されうる.
3.5.2. 出荷量制約#
「期間 \(t\) の製品 \(p\) の出荷量 \(z[p,t]\) が,所定の需要量以上でなければならない.」 ということを素直に立式すると,次式となる.
ここで \(D[p,t]\) は期間 \(t\) での製品 \(p\) の需要量である.
さて需要を超過した計画には何等の利得もなく,単なる過剰生産であるから, 次のように等式制約として記述すべきである.
3.6. 目的関数#
線形な定式化を図りたいので,目的関数は次の生産量および在庫量に線形な関数を想定する.
目的関数に付随する定数は,線形な定式化を大前提としているので,変数から定義されると考えてよい. 今の場合にはそれぞれ次の意味をもった定数 (コスト係数) が定式化に必要になっている.
\(COSTX[p]\) とは,製品 \(p\) を一単位生産するコスト
\(COSTY[p]\) とは,製品 \(p\) を一単位在庫とするコスト
ここで期間によってコスト係数は一定だと仮定した.
3.7. 求解#
あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる.
PySIMPLE Sample Code
1from pysimple import Problem, Set, Element, Parameter, Variable, Sum
2
3def optimize(method='higher'):
4 problem = Problem(name='production-planning-problem')
5
6 # Sets
7 MATERIALS = Set(dim=1, value=['A','B'])
8 m = Element(set=MATERIALS)
9 PRODUCTS = Set(dim=1, value=['I','II'])
10 p = Element(set=PRODUCTS)
11 TERMS = Set(dim=1, value=[1,2,3])
12 t = Element(set=TERMS)
13
14 # Variables
15 x = Variable(index=(p,t), lb=0)
16 y = Variable(index=(p,t), lb=0)
17 z = Variable(index=(p,t))
18 problem += z[p,1] == x[p,1] - y[p,1]
19 problem += z[p,2] == x[p,2] - y[p,2] + y[p,1]
20 problem += z[p,3] == x[p,3] - y[p,3] + y[p,2]
21
22 # Constraints
23 ## Consumption
24 C = Parameter(index=(m,p), value={
25 ('A', 'I'): 2,
26 ('B', 'I'): 5,
27 ('A', 'II'): 7,
28 ('B', 'II'): 3,
29 })
30 c = Sum(C[m,p]*x[p,t], p)
31 U = Parameter(index=(m,t), value={
32 ('A', 1): 920,
33 ('A', 2): 750,
34 ('A', 3): 500,
35 ('B', 1): 790,
36 ('B', 2): 600,
37 ('B', 3): 480,
38 })
39 problem += c[m,t] <= U[m,t], 'CoConsumption'
40
41 ## Demand
42 D = Parameter(index=(p,t), value={
43 ('I', 2): 60,
44 ('I', 3): 80,
45 ('II', 1): 20,
46 ('II', 2): 50,
47 ('II', 3): 90,
48 ('I', 1): 30,
49 })
50 problem += z[p,t] == D[p,t], 'CoDemand'
51
52 # Objective
53 COSTX = Parameter(index=p, value={
54 'I': 75,
55 'II': 50,
56 })
57 COSTY = Parameter(index=p, value={
58 'I': 8,
59 'II': 7,
60 })
61 problem += Sum(COSTX[p]*x[p,t]) + Sum(COSTY[p]*y[p,t]), 'TotalCost'
62
63 # Solve
64 problem.options.method = method
65 problem.solve()
66
67 # Print
68 print('\n[Print]')
69 print(x.val)
70 print(y.val)
71
72optimize()
上記を実行すると次の結果を得る.
Result
1
2[About Nuorium Optimizer]
3Nuorium Optimizer 24.1.0 build:614ca4b
4 <with META-HEURISTICS engine "wcsp"/"rcpsp">
5 <with Netlib BLAS>
6, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
7
8[Problem and Algorithm]
9PROBLEM_NAME production-planning-problem
10NUMBER_OF_VARIABLES 18
11NUMBER_OF_FUNCTIONS 19
12PROBLEM_TYPE MINIMIZATION
13METHOD HIGHER_ORDER
14
15[Progress]
16<preprocess begin>.........<preprocess end>
17<iteration begin>
18 res=1.8e+03 .... 7.2e-02 .. 1.5e-07
19<iteration end>
20
21[Result]
22STATUS OPTIMAL
23VALUE_OF_OBJECTIVE 21199.17241
24ITERATION_COUNT 8
25FUNC_EVAL_COUNT 11
26FACTORIZATION_COUNT 9
27RESIDUAL 1.477001532e-07
28CONSTRAINT_INFEASIBILITY 8.384404282e-13
29ELAPSED_TIME(sec.) 0.00
30
31[Print]
32x[I,1].val=37.99999999064992
33x[I,2].val=67.86206894777486
34x[I,3].val=64.13793106306763
35x[II,1].val=20.000000067138092
36x[II,2].val=86.8965517229395
37x[II,3].val=53.103448212069395
38y[I,1].val=7.999999990649923
39y[I,2].val=15.862068938424295
40y[I,3].val=1.4919209791011843e-09
41y[II,1].val=6.713808929802791e-08
42y[II,2].val=36.89655179007676
43y[II,3].val=2.146803068218254e-09
求解結果から在庫量について次のことが確認できる.
y[I,3]とy[II,3]がほぼ \(0\) である.
これらは「下限について非負制約以外の制約がないこと」
および「目的関数 TotalCost が最小化であること」の二つが原因である.
よってもしあらかじめ最後の期間について,次のように y[p,3] 自体を消し去ったとしても一般性が失われないことになる.
これによって最後の期間についての変数を削減できるとわかる.
3.8. 改良すべき点#
定式化の改良はプログラミング言語でいうところのハードコーディング部分を探し出して潰すことである. この観点で見ると,今の場合には以下の点が該当する.
期間が 3 か月 (四半期基準) であることを前提にしている.よって半年であるとか一年といった生産計画を柔軟に計算できない.定式化の修正が必要になってしまう.
よって,計画期間が変化した場合でも対応できるようにしたモデルを考える余地があるとわかる. このようにして,適宜,モデルの表現能力を汎化させていくとよい.
引用書式
