Ctrl+K

ナンバープレイス

2. ナンバープレイス#

2.1. 背景#

ナンバープレイスは米国ニューヨークにかつてあった Dell Magazines という出版社が 1979 年に発行した PENCIL PUZZLES & WORD GAMES の 5 月号に掲載されたのが始まりだとされている． 考案者は建築家の Howard Garns であったという．

与えられたナンバープレイスを数理最適化の割当問題として定式化することは， 他のいろいろな割当問題を扱う前に，様々な考え方を紹介する手頃な例題として有用である．

なお，ナンバープレイスを計算機で解かせることにそれほど大きな困難はないが， だからといって，ナンバープレイスの面白さが色褪せることはない． ナンバープレイスはいかに人間が考えさせられる問題を作問し，それらを手で解いていく中であたかもコミュニケーションをするかのような体験をすることに面白さがある [3]． ここではあくまでも，割当問題の概念などを説明するために，ナンバープレイスを例題として引用することとしている．

2.2. 設定#

2.3. 問題設定からの読み取り#

設定で与えたナンバープレイスの規則を読めば，すべての規則が書かれている印象を受ける． また実業務と異なり，広く認知されている題材であるため，制約条件が共通認識として予め明らかにされている点が今回は著しい． そこで本例題では，定式化がある程度は機械的にできることを述べるために， 与えられた規則をもう少し補足して，制約条件文から何を読み取っていけばよいかを考察することにする．

まず与えられた規則からの制約条件式の立式が，より容易になるよう，次のように文を補う．

  • マス目には 1 ～ 9 の数が 何れか 1 つ 入る

  • 列には 1 ～ 9 の数のいずれかが 1 つずつ重複なく 入る

  • 行には 1 ～ 9 の数のいずれかが 1 つずつ重複なく 入る

  • 太線で囲まれた 3×3 のブロック内には 1 ～ 9 の数の何れかが 1 つずつ 重複なく 入る

マス目に数が 1 つしか入らないことは暗黙の了解だったかもしれないが，ここではそれを補っている． またナンバープレイスでは幾つかのマスに数が既に入っており， この数の配置と矛盾がないように，数を埋めていかなければならない． このことは当たり前すぎる前提だが，紛れもなく一つの重要な規則であり， 定式化に必要な文を作っておく必要がある．それが次である．

  • すでに与えられている数の配置は変えてはならない (明文化されにくい暗黙の制約条件)

こうしてナンバープレイスを定式化するうえで必要な文をすべて作文できた．

まずすぐにわかることは，これら規則には目的関数に相当する最適化すべき指標がどこにもないということである． それ故，目的関数が存在しない問題であることがわかる．

注釈

数理最適化というと，必ず目的関数があるかのように思われるかもしれないが， 制約条件だけを満たす解 (実行可能解) を見つけるだけの問題であれば， 目的関数は必ずしも必要がない．

規則文をよく整理することで，何が「制約条件」と (今回は存在しないが) 「目的関数」となるのかが， 明瞭になっていくため，どのような集合や変数を考えれば良いのかという，定式化要素が自然と決まってきやすい．

2.4. 集合・要素，変数および定数の読み取り#

整理した設定から「集合・要素」「変数」「定数」に相当する文を次のように読み取ることができる．

集合・要素

マス目・行・列・1 ～ 9 の数・3×3 のブロック

  • 1 ～ 9 の数 → 値 \(v\in V:=\{1,2,3,4,5,6,7,8,9\}\)

  • 行 → 行番号 \(r\in R:=\{1,2,3,4,5,6,7,8,9\}\)

  • 列 → 列番号 \(c\in C:=\{1,2,3,4,5,6,7,8,9\}\)

  • 3×3 のブロック → \((n,r,c)\in B:=\{(ブロック番号, 行番号, 列番号)\}\)

注釈

ブロック番号は下図のように割り当てる． このため例えばブロック番号 \(n=3\) である \(B\) の要素は， \((3,1,7),(3,1,8),(3,1,9),(3,2,7),(3,2,8),(3,2,9),(3,3,7),(3,3,8),(3,3,9)\) となる．

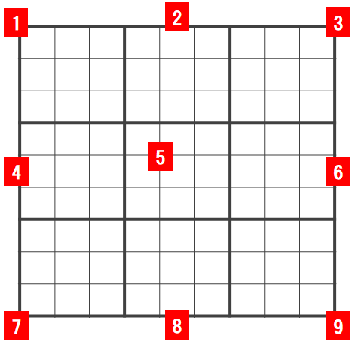
ブロック番号

図 2.2 ブロック番号#

変数

入る

  • 入る・入らない → 2 値選択 → \(1\) or \(0\) のバイナリ変数 x

  • \(x[(v,r,c)]\): 値 \(v\) を \(r\) 行 \(c\) 列に入れるか否か

定数 (入力データ)

数の初期配置 (すでに与えられている数の配置)

  • 初期配置 → 初期配置集合 \(INIT\)

  • \(1\) 行目 \(1\) 列目には予め値 \(5\) が配置されているならば，\((5,1,1)\in INIT\) であることを意味する

初期配置

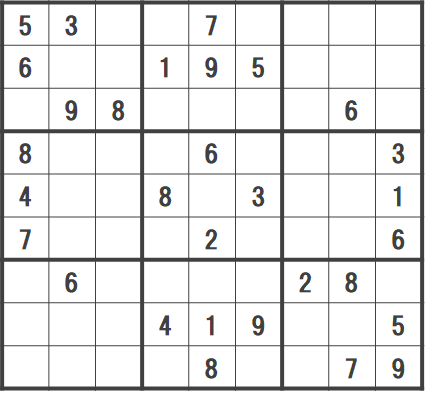
図 2.3 初期配置#

制約条件文は「S が C の下で V である」となっているパターンである． 変数の詳細化のヒントとも解釈できる．

観点

S

C

V

クラス

集合・要素

---

変数

変数関数

添字 (定義域)

制約条件式の形

値域

2.5. 制約条件の立式#

マス目 \((r,c)\) には 1 ～ 9 の数 \(v\) が何れか 1 つ入る

(1)#\[\sum_{v\in V}x[v,r,c] = 1,\quad \forall r\in R,~ \forall c\in C\]

列 \(c\) には 1 ～ 9 の数 \(v\) の何れかが 1 つずつ重複なく入る

(2)#\[\sum_{r\in R}x[v,r,c] = 1,\quad \forall v\in V,~ \forall c\in C\]

行 \(r\) には 1 ～ 9 の数 \(v\) の何れかが 1 つずつ重複なく入る

(3)#\[\sum_{c\in C}x[v,r,c] = 1,\quad \forall v\in V,~ \forall r\in R\]

太線で囲まれた 3×3 のブロック内には 1 ～ 9 の数 \(v\) の何れかが 1 つずつ重複なく入る

(4)#\[\sum_{(r,c)\mid (n,r,c)\in B} x[v,(r,c)] = 1,\quad \forall v\in V,~ \forall n \in \mathrm{slice}_1(B)\]

Tip

ブロック集合 \(B\) は単純な直積になっていない．実際の定式化にあたってはこのような直積でない多次元集合が頻出する． こういった集合に対して，\(k\) 番目にある要素を集めてできる集合が必要になることがしばしばある． 例えばブロック集合 \(B\) の \(1\) 番目の要素を集めてできる集合とは，ブロック番号 \(1\) から \(9\) までからなる集合である． 今，このブロック番号からなる集合を \(N\) と書くとき，\(B\) と \(N\) の関係は「射影」の関係にある． 我々はこの「射影」について，もう少し広い概念を込めてスライスともよんでいる． これらについての詳細は『`射影とスライス`_』で述べている．

すでに与えられている数の配置は変えてはならない

(5)#\[x[v,r,c] = 1,\quad \forall (v,r,c) \in INIT\]

2.6. 求解#

あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる．

(6)#\[\begin{split}\sum_{v\in V}x[v,r,c] &= 1,\quad \forall r\in R,~ \forall c\in C, \\ \sum_{r\in R}x[v,r,c] &= 1,\quad \forall v\in V,~ \forall c\in C, \\ \sum_{c\in C}x[v,r,c] &= 1,\quad \forall v\in V,~ \forall r\in R, \\ \sum_{(r,c)\mid (n,r,c)\in B} x[v,(r,c)] &= 1,\quad \forall v\in V,~ \forall n \in \mathrm{slice}_1(B), \\ x[v,r,c] &= 1,\quad \forall (v,r,c) \in INIT\end{split}\]
PySIMPLE Sample Code
 1def show_table(R, C, V, table):
 2    from sys import stdout
 3
 4    for r, in R:
 5        if r in (1, 4, 7):
 6            stdout.write("+-------+-------+-------+\n")
 7        for c, in C:
 8            for v, in V:
 9                if table[v,r,c] == 1:
10                    break
11            else:
12                v = ' '
13            if c in (1, 4, 7):
14                stdout.write("| ")
15            stdout.write(str(v) + " ")
16        stdout.write("|\n")
17    stdout.write("+-------+-------+-------+\n")
18
19def optimize(**kwds):
20    from pysimple import Problem, Set, Element, BinaryVariable, Sum, Parameter
21
22    # Sets & Elements
23    V = R = C = Set(value=range(1, 10))
24    v = Element(set=V)
25    r = Element(set=R)
26    c = Element(set=C)
27    Blocks = Set(value=[(s+1, s//3*3+t//3+1, s%3*3+t%3+1) for s in range(9) for t in range(9)])
28    b = Element(set=Blocks)  # b(0) は Block 番号
29
30    INIT = Set(value=[(5, 1, 1), (6, 2, 1), (8, 4, 1), (4, 5, 1), (7, 6, 1), (3, 1, 2), (9, 3, 2), (6, 7, 2), (8, 3, 3), (1, 2, 4), (8, 5, 4), (4, 8, 4), (7, 1, 5), (9, 2, 5), (6, 4, 5), (2, 6, 5), (1, 8, 5), (8, 9, 5), (5, 2, 6), (3, 5, 6), (9, 8, 6), (2, 7, 7), (6, 3, 8), (8, 7, 8), (7, 9, 8), (3, 4, 9), (1, 5, 9), (6, 6, 9), (5, 8, 9), (9, 9, 9)])
31    init_vrc = Element(set=INIT)
32
33    # Variables
34    x = BinaryVariable(index=(v,r,c))  # 値 v が (r,c) に入るか
35
36    # Constraints
37    prob = Problem(name='Number Place', type=max)
38    prob += Sum(x[v,r,c], v) == 1          # 各マスにはいずれかの値
39    prob += Sum(x[v,r,c], r) == 1          # 各値は各列のいずれか
40    prob += Sum(x[v,r,c], c) == 1          # 各値は各行のいずれか
41    prob += Sum(x[v,b(1,2)], b(1,2)) == 1  # 各値は各ブロックのいずれか
42    prob += x[init_vrc] == 1               # 初期条件
43
44    # Solve
45    prob.solve(**kwds)
46
47    # Print
48    print('\n[Print]')
49    inittable = Parameter(index=(v,r,c), value=dict.fromkeys(INIT, 1))
50    resulttable = dict(x.val.items())  # dump as dict
51    print('initial pattern')
52    show_table(R, C, V, inittable)
53    print('result pattern')
54    show_table(R, C, V, resulttable)
55    return
56
57optimize()

上記を実行すると次の結果を得る．

Result
  1
  2[About Nuorium Optimizer]
  3Nuorium Optimizer 24.1.0 build:614ca4b
  4	 <with META-HEURISTICS engine "wcsp"/"rcpsp">
  5	 <with Netlib BLAS>
  6, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
  7
  8[Problem and Algorithm]
  9PROBLEM_NAME                                     Number Place
 10NUMBER_OF_VARIABLES                                       729
 11(#INTEGER/DISCRETE)                                       729
 12NUMBER_OF_FUNCTIONS                                       354
 13PROBLEM_TYPE                                     MAXIMIZATION
 14METHOD                                                SIMPLEX
 15
 16[Progress]
 17<preprocess begin>.........<preprocess end>
 18<iteration begin>
 19Coefficient Statistics (original problem)
 20  Coefficient range         [min,max] : [1.00e+00,1.00e+00]
 21  RHS and bounds            [min,max] : [1.00e+00,1.00e+00]
 22  Objective                 [min,max] : [0.00e+00,0.00e+00]
 23Coefficient Statistics (after scaling)
 24  Coefficient range         [min,max] : [1.00e+00,1.00e+00]
 25  RHS and bounds            [min,max] : [1.00e+00,1.00e+00]
 26  Objective                 [min,max] : [0.00e+00,0.00e+00]
 27  Row scaling range         [min,max] : [-1.00e+00,1.00e+00]
 28  Column scaling range      [min,max] : [1.00e+00,1.00e+00]
 29
 30<<wcsp tabu search begin>>
 31  number of column singleton : 0
 32  number of column selection : 76
 33  Modify coefficients 
 34
 35<preprocess begin>..........<preprocess end>
 36preprocessing time: 0(s) 
 37<iteration begin>
 38--- TryCount = 1 ---
 39# random seed = 1
 40(hard/semihard/soft) penalty= 261/0/0, time= 0.00(s)
 41<greedyupdate begin>..........<greedyupdate end>
 42greedyupdate time= 0.001(s)
 43(hard/semihard/soft) penalty= 87/0/0, time= 0.00(s), iteration= 0
 44(hard/semihard/soft) penalty= 83/0/0, time= 0.00(s), iteration= 1
 45(hard/semihard/soft) penalty= 79/0/0, time= 0.00(s), iteration= 2
 46(hard/semihard/soft) penalty= 75/0/0, time= 0.00(s), iteration= 3
 47(hard/semihard/soft) penalty= 73/0/0, time= 0.00(s), iteration= 4
 48(hard/semihard/soft) penalty= 71/0/0, time= 0.00(s), iteration= 5
 49(hard/semihard/soft) penalty= 69/0/0, time= 0.00(s), iteration= 6
 50(hard/semihard/soft) penalty= 67/0/0, time= 0.00(s), iteration= 7
 51(hard/semihard/soft) penalty= 63/0/0, time= 0.00(s), iteration= 8
 52(hard/semihard/soft) penalty= 61/0/0, time= 0.00(s), iteration= 9
 53(hard/semihard/soft) penalty= 59/0/0, time= 0.00(s), iteration= 10
 54(hard/semihard/soft) penalty= 57/0/0, time= 0.00(s), iteration= 11
 55(hard/semihard/soft) penalty= 55/0/0, time= 0.00(s), iteration= 12
 56(hard/semihard/soft) penalty= 53/0/0, time= 0.00(s), iteration= 13
 57(hard/semihard/soft) penalty= 51/0/0, time= 0.00(s), iteration= 14
 58(hard/semihard/soft) penalty= 49/0/0, time= 0.00(s), iteration= 15
 59(hard/semihard/soft) penalty= 48/0/0, time= 0.00(s), iteration= 16
 60(hard/semihard/soft) penalty= 46/0/0, time= 0.00(s), iteration= 19
 61(hard/semihard/soft) penalty= 44/0/0, time= 0.00(s), iteration= 22
 62(hard/semihard/soft) penalty= 42/0/0, time= 0.00(s), iteration= 24
 63(hard/semihard/soft) penalty= 40/0/0, time= 0.00(s), iteration= 25
 64(hard/semihard/soft) penalty= 36/0/0, time= 0.00(s), iteration= 29
 65(hard/semihard/soft) penalty= 34/0/0, time= 0.00(s), iteration= 49
 66(hard/semihard/soft) penalty= 32/0/0, time= 0.00(s), iteration= 65
 67(hard/semihard/soft) penalty= 30/0/0, time= 0.00(s), iteration= 68
 68(hard/semihard/soft) penalty= 26/0/0, time= 0.00(s), iteration= 96
 69(hard/semihard/soft) penalty= 25/0/0, time= 0.00(s), iteration= 145
 70(hard/semihard/soft) penalty= 23/0/0, time= 0.00(s), iteration= 168
 71(hard/semihard/soft) penalty= 22/0/0, time= 0.00(s), iteration= 171
 72(hard/semihard/soft) penalty= 21/0/0, time= 0.00(s), iteration= 206
 73(hard/semihard/soft) penalty= 18/0/0, time= 0.00(s), iteration= 227
 74(hard/semihard/soft) penalty= 17/0/0, time= 0.01(s), iteration= 451
 75(hard/semihard/soft) penalty= 16/0/0, time= 0.01(s), iteration= 501
 76(hard/semihard/soft) penalty= 15/0/0, time= 0.01(s), iteration= 503
 77(hard/semihard/soft) penalty= 11/0/0, time= 0.01(s), iteration= 512
 78(hard/semihard/soft) penalty= 10/0/0, time= 0.01(s), iteration= 607
 79(hard/semihard/soft) penalty= 7/0/0, time= 0.01(s), iteration= 906
 80<<AlgWcsp>> adjusted maxIterationCurrent = 2000 (ratio = 0.9060 > 0.8000)
 81(hard/semihard/soft) penalty= 6/0/0, time= 0.01(s), iteration= 1240
 82(hard/semihard/soft) penalty= 5/0/0, time= 0.01(s), iteration= 1757
 83(hard/semihard/soft) penalty= 3/0/0, time= 0.01(s), iteration= 1963
 84<<AlgWcsp>> adjusted maxIterationCurrent = 3000 (ratio = 0.9815 > 0.8000)
 85# (hard/semihard/soft) penalty= 3/0/0
 86# time = 0.01/0.02(s)
 87# iteration = 1963/3000
 88<iteration end>
 89# (hard/soft) = 3/0
 90# iteration = 3000
 91# time =  0.02 (s), succ = 0
 92<<wcsp tabu search end>>
 93
 94
 95        1.2
 96
 97#sol         upper         lower   gap(%)  time(s)  list  mem(MiB)
 98#1              -0            -0    0.000      0.0     1       747  sol: relax 
 99                -0            -0    0.000      0.0     0       747
100
101<iteration end>
102
103[Result]
104STATUS                                                OPTIMAL
105VALUE_OF_OBJECTIVE                                          0
106SIMPLEX_PIVOT_COUNT                                         0
107PARTIAL_PROBLEM_COUNT                                       1
108ELAPSED_TIME(sec.)                                       0.03
109
110[Print]
111initial pattern
112+-------+-------+-------+
113| 5 3   |   7   |       |
114| 6     | 1 9 5 |       |
115|   9 8 |       |   6   |
116+-------+-------+-------+
117| 8     |   6   |     3 |
118| 4     | 8   3 |     1 |
119| 7     |   2   |     6 |
120+-------+-------+-------+
121|   6   |       | 2 8   |
122|       | 4 1 9 |     5 |
123|       |   8   |   7 9 |
124+-------+-------+-------+
125result pattern
126+-------+-------+-------+
127| 5 3 4 | 6 7 8 | 9 1 2 |
128| 6 7 2 | 1 9 5 | 3 4 8 |
129| 1 9 8 | 3 4 2 | 5 6 7 |
130+-------+-------+-------+
131| 8 5 9 | 7 6 1 | 4 2 3 |
132| 4 2 6 | 8 5 3 | 7 9 1 |
133| 7 1 3 | 9 2 4 | 8 5 6 |
134+-------+-------+-------+
135| 9 6 1 | 5 3 7 | 2 8 4 |
136| 2 8 7 | 4 1 9 | 6 3 5 |
137| 3 4 5 | 2 8 6 | 1 7 9 |
138+-------+-------+-------+

2.7. 解の一意性#

求解で得られた解の唯一性を判定するにはどうすればよいだろうか．

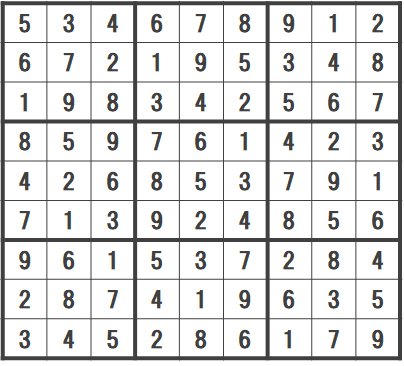
求解で得られた解

図 2.4 求解で得られた解#

ナンバープレイスでは次のことが知られている．

初期配置の個数が \(17\) 個で初めて唯一解が存在する． つまり \(16\) 個以下はどうやっても解は \(2\) パターン以上存在する．

よって今回の初期配置の個数は \(30\) 個であるため，解が唯一解である可能性がある． これを調べたい．それは次の考えで行う．

解が唯一つかどうかを判定すればよいので，次のようにすると判定できる．

  1. 解を 1 つ得ておく．(解の存在)

  2. すでに得た解を禁止する制約を課す．

  3. 求解して解が得られなかったら，「禁止した解が唯一の解だった」とわかる．

順にこれを見ていこう．

求解して得られた解を \(X\) としよう．

(7)#\[X[1,1,1] = 0,~ X[2,1,1] = 0,~ \cdots,~ X[5,1,1] = 1,~ \cdots,~ X[9,9,9] = 1.\]

次に上記の解 \(X\) を禁止する制約条件を課したい． このような場合にはすべて同じ配置であった場合 のみ を禁止する必要があり， 次の定式化を行うことになる．

(8)#\[\begin{split}ANS := \{(v,r,c)\mid X[v,r,c] = 1\}, \\ \sum_{(v,r,c)\in ANS} x[v,r,c] \leq |ANS| - 1\end{split}\]

これは \(1\) が立つ \(|ANS|\) 個の箇所すべてについて， 既出の解 \(X\) と同じ箇所が採用されてしまうと， 制約条件式を満たせなくなってしまうことを記述している． 一箇所以上異なっていれば，制約条件違反とはならない． つまりこれは我々が欲しい制約条件式である．

なお，この話題については，次のように定式化してしまいがちであり，注意が必要である．

注意

次の制約条件式は解である場合には \(x = 0\) で禁止され， 解でない場合には \(x \leq 1\) で \(x\) が自由になっている．

(9)#\[x[v,r,c] \leq 1 - X[v,r,c]\]

一見，所望の制約条件式が書けたように思われる． しかしこの制約条件だと，一箇所でも前の解と同じ配置になると制約違反となってしまう．

もしこのまま求解すれば，解を得ることはより難しくなってしまう． そしてこの誤りに気付かないと，解の一意性を誤って示したことになってしまう． このようなところが数理最適化の難しさの一つでもある．

2.8. 問題拡張への対応#

数理最適化による問題解決の利点として，仕様変更に強いことが挙げられることがある． このことを以下に述べる X 条件というものを通して見てみる．

これまで扱ってきたナンバープレイスに対して，次の X 条件が追加された場合にはどうすればよいだろうかを考える．

  • 対角線には 1 ～ 9 の数のいずれかが 1 つずつ重複なく入る．

X 条件

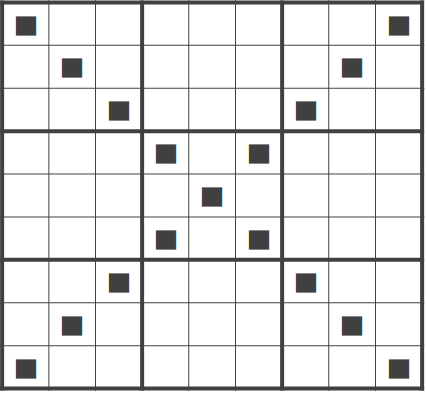
図 2.5 X 条件#

今回追加された X 条件の定式化そのものは，次の 2 つの制約条件式によって容易に記述できる．

(10)#\[\begin{split}\sum_{r\in R} x[v,r,r] &= 1, \\ \sum_{r\in R} x[v,r,|C|-r+1] &= 1\end{split}\]

さてこれは重要なことだが，仕様変更では単純に変更内容だけが問題にはならない． 例えば今のように追加要件を実現することだけで完結しない． というのも，これまで解けていた問題が解けなくなってしまうことがあるからだ． このことは仕様変更で頻出する話題であろう．

注釈

新たに制約条件を追加すると， これまでの入力データに対して解なし (infeasible) となる場合がよくある． 条件の追加によって，より厳しくなるためである．

このことと関連して (今回，目的関数はないが) 目的関数値も条件を追加するほど最適値が悪くなっていく．

実際，これまでに扱ってきた与えられた初期配置では X 条件を満たす解は存在しない． さてそうなると，初期配置 (入力データ) のどこに不備があるのか，ということに興味が行くことになる． よって次のことが新たに問題として設定されやすい．

  • 可能な限り初期配置を尊重した解を計算するようにしなさい．

数理最適化ではこの問題を定式化の範疇でアプローチできるという点が著しい． それは次のような考えである．

  1. 破れている制約条件を緩和する．緩和の程度は変数に担わせる．

    今の場合，初期配置の制約条件を次のように書き換える． ここで \(y\) は \(0\) か \(1\) をとる新たなバイナリ変数である．

    (11)#\[x[v,r,c] = y[v,r,c],\quad \forall (v,r,c)\in INIT\]

  2. 緩和の最小化を目的関数として設定する．

    今の場合，\(y\) がすべて \(1\) をとれば， 初期配置をすべて満たすことになるため，次の目的関数の最大化を設定する．

    (12)#\[\mathrm{Maximize:}~ \sum_{p,t} COSTX[p] \cdot x[p,t] + \sum_{p,t} COSTY[p] \cdot y[p,t]\]

以上により，可能な限り初期配置を尊重した解が計算されることとなる．

注釈

「解なし」で捨てずに「制約を破るとしてもどこまで粘れるか」がしばしば重要になる． 目的関数は必ずしも要件に明示的に表れる最適化指標だけに限らない．

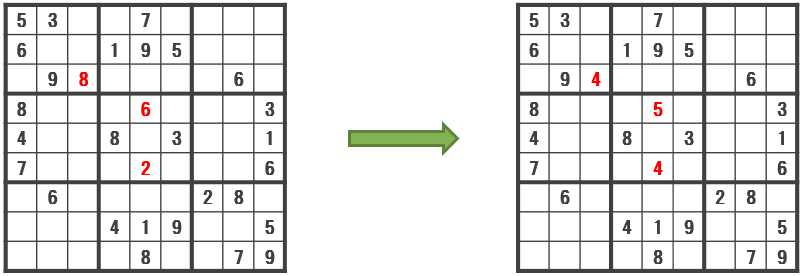
最適化計算を実行すると，3 箇所だけ初期配置が欠けた答えを算出する．

図 2.6 最適化計算を実行すると，3 箇所だけ初期配置が欠けた答えを算出する．#

まとめると，仕様変更の強さとしては以下の点を挙げることができる．

  • 制約条件式を元の定式化に付加的に追加するだけでよい場合があること

  • 相互の矛盾が発生した場合にはソフト制約の概念を導入して定量的に矛盾を解決できること

技法集

参考文献

[1]

Nobuhiko Kanamoto. Why hand made? URL: https://www.nikoli.co.jp/en/puzzles/sudoku/why_hand_made/.

[2]

Jean-Paul Delahaye. The Science behind Sudoku. Scientific American, 294(6):80–87, jun 2006. URL: https://www.cs.virginia.edu/$\sim$robins/The_Science_Behind_SudoKu.pdf, doi:10.1038/scientificamerican0606-80.

引用書式

BibTeX

目次