3. 積み付け#
3.1. 背景#
物流を構成する一連の営みの中で，貨物を如何にして輸送機関に無駄なく詰め込むかという問題があり， この種の問題全般を積み付け問題とよぶことにする． 積み付け問題では「海上輸送」「航空輸送」「鉄道輸送」「陸上輸送」など様々な輸送形態があり， そのそれぞれに特色ある制約条件を考慮しなければならない．
いずれも積み付けた貨物を「運ぶ」ため，荷崩れしないことは勿論だが， 荷造り・荷解きといったことも重要な観点となってくる．
そのようなことから，単純に「入りきるか」という観点だけでは実用上有益な解は得られず， どのように積み付けるかという種々の「配置制約」が非常に重要になってくる．
ここでは「\(i\) は \(j\) の左側に位置する」といった意味での配置制約について言及する．
注釈
「積み付け問題」という用語は「箱詰め問題」もしくは同義語としての「ビンパッキング問題」という用語に対して， 配置制約を更に加味した問題というより広い意味をここでは持たせている． ここでビンパッキング問題は次で定義されるものとする．
アイテムには形状から定まるサイズが定められており， これらを用意された複数個のビンに重なりなく詰め込むとき， 必要なビンの個数を最小にする詰め込み方を決定する問題である．
3.2. 設定#
3.3. 集合#
今回考える問題はビンが \(1\) つのため，集合としてはアイテム集合 \(I\) のみを考える．
3.4. 定数#
3.5. 変数#
- アイテムの配置座標 (長方形の左下の頂点座標) \((x,y)\)
- (4)#\[\begin{split}x[i] &\in \mathbb{R}_{\geq 0}, \\ y[i] &\in \mathbb{R}_{\geq 0}\end{split}\]
3.6. 制約条件#
まず次の制約条件については容易に設定できる．
- ビンからはみ出さない．
- (5)#\[\begin{split}x[i] + ITEM\_W[i] &\leq BIN\_W, \\ y[i] + ITEM\_H[i] &\leq BIN\_H\end{split}\]
今回の定式化の要点は次の制約条件にある．
アイテムが重ならない．
以下ではこれを特に取り上げる．
3.6.1. 配置制約#
\(2\) つのアイテム \(i_1\) と \(i_2\) が重ならないためには， \(i_1 < i_2\) であるとして，次の何れかが満たされていればよい．
これらは上から順に以下の配置制約をそれぞれ表している．
\(i_1\) は \(i_2\) の左側に位置する．
\(i_1\) は \(i_2\) の右側に位置する．
\(i_1\) は \(i_2\) の下側に位置する．
\(i_1\) は \(i_2\) の上側に位置する．
さてここで「\(i_1\) は \(i_2\) の左側に位置する．」「\(i_1\) は \(i_2\) の右側に位置する．」とは両立しない． このことは式からもわかる．上下の関係についても同様である．
また仮に「\(i_1\) は \(i_2\) の左側に位置する．」が成立した場合には， 上下について何れの制約条件が成立しても，もしくは何れも成立していなくても構わないようになっている． このことは \(2\) 次元的な配置関係を考える上では矛盾がない論理関係である．
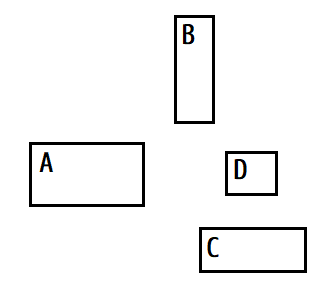
図 3.2 長方形 A は 長方形 B および長方形 C の左側に位置しており，かつ，長方形 A は長方形 B の下側および長方形 C の上側に位置した配置関係になっている．加えて長方形 A は長方形 D の左側に位置しているが，長方形 A は長方形 D の下側でも上側でもない．#
以上からこれらの特徴を加味した制約条件式を書き下す必要があるとわかる．
3.6.2. 制約条件の修正#
そこでまず新たな論理変数 \(z\) を導入して，次のように制約条件式を書き換える． 追加した右辺第 \(2\) 項は Big M になっていることに注意する．
導入した論理変数 \(z\) は次の意味を持っている．
\(z[(i_1,r,i_2)]\): \(i_1\) は \(i_2\) の \(r\) 側にある．
\(r\) は \(2\) つの長方形の位置関係を与えるものであり，これを位置関係集合 \(RELATIONS\) として定式化しておく．
この上で次の配置関係集合を定義しておくと，定式化の記述が見通し良くなる．
論理変数 \(z\) の添字はこの配置関係集合の元を添字にもつ．
ここまでで，左右または上下の配置関係に対する制約条件についての両立の問題が解消されている． 例えば「\(i_1\) は \(i_2\) の左側に位置する．」が成立した場合には， 「\(i_1\) は \(i_2\) の右側に位置する．」が成立してはならない． このことは「\(z[(i_1,\mathrm{LEFT},i_2)]\) が \(0\) または \(1\)」かつ「 \(z[(i_1,\mathrm{RIGHT},i_2)]=0\)」として表現できている．上下についても同様である．
しかし各 \(i_1\) および \(i_2\) についてのすべての論理変数 \(z\) が \(0\) になる場合を許容している．
この場合は配置座標 \((x,y)\) が自由変数となってしまうため，長方形同士が重なり合ってしまう場合を許容していることになる． このような場合を回避するために，次の制約条件を追加で課す．
つまり繰り返しとなるが，仮に「\(i_1\) は \(i_2\) の左側に位置する．」が成立した場合には， 上下について何れの制約条件が成立しても，もしくは何れも成立していなくても構わないため，高々 \(1\) つの論理変数が \(1\) になれば十分である． それ故に上記の制約条件でよいとわかる．
3.7. 目的関数#
今回考える問題はビンに入りきりさえすればよいので， 制約条件をすべて満たす解であれば，所望する解になっている．
そこで目的関数を設定せずに，このまま求解してみると， 得られる結果は原点に可能な限り寄せた解が得られるとは限らない．
このため今まで行った定式化だけからでは，後処理が場合によっては必要となる． 定式化で考慮するならば，次の目的関数を設定すればよい．
このように設定すれば，後処理をすることなく， ビンに入りきるもののうち，なるべく原点に近いパターンが採用されることになる．
しかしながら，問題としてはビンに入りきりさえすればよいので， 制約条件がすべて満たされた時点で求解を終えて， 頂点座標の平行移動については最適化計算とは別の後処理として行うことが望ましいと考えられる．
注釈
今回は簡単のため，ビンの数を \(1\) つに限ったが，入りきらない場合も想定すれば， ビンの数は複数仮定してその数を最小化したほうが実務的にも自然である． というのも，後どれだけビンが必要かという観点で，求解結果を解釈できるからである．
3.8. 求解#
あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる．
PySIMPLE Sample Code
1def optimize(**kwds):
2 from pysimple import Problem, Set, Element, BinaryVariable, Variable, Sum, Parameter, Condition
3
4 # アイテム集合
5 ITEMS = Set(value=range(1,9))
6 i = Element(set=ITEMS)
7 i1 = Element(set=ITEMS)
8 i2 = Element(set=ITEMS)
9
10 # 位置関係集合
11 RELATIONS = Set(value=['IS_LEFT_OF', 'IS_RIGHT_OF', 'IS_UPPER_OF', 'IS_LOWER_OF'])
12 r = Element(set=RELATIONS)
13
14 # ビン & アイテムのサイズ
15 BIN_W = Parameter(value=6)
16 BIN_H = Parameter(value=6)
17 ITEM_W = Parameter(index=i, value={1:1, 2:1, 3:2, 4:2, 5:3, 6:3, 7:2, 8:3})
18 ITEM_H = Parameter(index=i, value={1:1, 2:2, 3:2, 4:1, 5:2, 6:3, 7:4, 8:1})
19
20 # 配置関係集合
21 iri = Condition((i1,r,i2), i1 < i2)
22
23 # 1 ならば条件が真
24 z = BinaryVariable(index=iri)
25
26 # アイテム i の位置
27 x = Variable(index=i, lb=0)
28 y = Variable(index=i, lb=0)
29
30 prob = Problem(name='Packing', type=min)
31
32 # ビンからはみ出ない
33 prob += x[i] + ITEM_W[i] <= BIN_W
34 prob += y[i] + ITEM_H[i] <= BIN_H
35
36 # RELATIONS のどれかが成りたたなければいけない
37 prob += Sum(z[iri], iri(1)) >= 1
38
39 # z[i1,'IS_LEFT_OF',i2] == 1 ならば x[i1] + ITEM_W[i1] <= x[i2]
40 iri_LEFT = Condition(iri, iri(1) == 'IS_LEFT_OF')
41 prob += x[iri_LEFT(0)] + ITEM_W[iri_LEFT(0)] <= x[iri_LEFT(2)] + BIN_W * (1 - z[iri_LEFT])
42
43 # z[i1,'IS_RIGHT_OF',i2] == 1 ならば x[i2] + ITEM_W[i2] <= x[i1]
44 iri_RIGHT = Condition(iri, iri(1) == 'IS_RIGHT_OF')
45 prob += x[iri_RIGHT(2)] + ITEM_W[iri_RIGHT(2)] <= x[iri_RIGHT(0)] + BIN_W * (1 - z[iri_RIGHT])
46
47 # z[i1,'IS_LOWER_OF',i2] == 1 ならば y[i1] + ITEM_H[i1] <= y[i2]
48 iri_LOWER = Condition(iri, iri(1) == 'IS_LOWER_OF')
49 prob += y[iri_LOWER(0)] + ITEM_H[iri_LOWER(0)] <= y[iri_LOWER(2)] + BIN_H * (1 - z[iri_LOWER])
50
51 # z[i1,'IS_UPPWE_OF',i2] == 1 ならば y[i1] + ITEM_H[i1] <= y[i2]
52 iri_UPPER = Condition(iri, iri(1) == 'IS_UPPER_OF')
53 prob += y[iri_UPPER(2)] + ITEM_H[iri_UPPER(2)] <= y[iri_UPPER(0)] + BIN_H * (1 - z[iri_UPPER])
54
55 prob += Sum(x[i] + y[i], i)
56
57 # Solve
58 prob.solve(**kwds)
59
60 # Print
61 print('\n[Print]')
62 for i, in ITEMS:
63 print(i, round(x[i].val, 0), round(y[i].val, 0))
64
65optimize()
上記を実行すると次の結果を得る．
Result
1[About Nuorium Optimizer]
2Nuorium Optimizer 24.1.1 build:ff97c72
3 <with META-HEURISTICS engine "wcsp"/"rcpsp">
4 <with Netlib BLAS>
5, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
6
7[Problem and Algorithm]
8PROBLEM_NAME Packing
9NUMBER_OF_VARIABLES 128
10(#INTEGER/DISCRETE) 112
11NUMBER_OF_FUNCTIONS 157
12PROBLEM_TYPE MINIMIZATION
13METHOD SIMPLEX
14
15[Progress]
16<preprocess begin>.........<preprocess end>
17<iteration begin>
18Coefficient Statistics (original problem)
19 Coefficient range [min,max] : [1.00e+00,6.00e+00]
20 RHS and bounds [min,max] : [1.00e+00,5.00e+00]
21 Objective [min,max] : [1.00e+00,1.00e+00]
22Coefficient Statistics (after scaling)
23 Coefficient range [min,max] : [1.00e+00,1.00e+00]
24 RHS and bounds [min,max] : [3.33e-01,1.00e+00]
25 Objective [min,max] : [8.00e+00,8.00e+00]
26 Row scaling range [min,max] : [1.67e-01,1.33e+00]
27 Column scaling range [min,max] : [1.67e-01,1.00e+00]
28
29<<wcsp tabu search begin>>
30 number of column singleton : 0
31 number of column selection : 0
32 Modify coefficients
33
34<preprocess begin>..........<preprocess end>
35preprocessing time: 0(s)
36<iteration begin>
37--- TryCount = 1 ---
38# random seed = 1
39(hard/semihard/soft) penalty= 64/0/0, time= 0.00(s)
40<greedyupdate begin>..........<greedyupdate end>
41greedyupdate time= 0(s)
42(hard/semihard/soft) penalty= 28/0/0, time= 0.00(s), iteration= 0
43# (hard/semihard/soft) penalty= 28/0/0
44# time = 0.00/0.00(s)
45# iteration = 0/1000
46<iteration end>
47# (hard/soft) = 28/0
48# iteration = 1000
49# time = 0.00 (s), succ = 0
50<<wcsp tabu search end>>
51
52
53 .12
54
55#sol upper lower gap(%) time(s) list mem(MiB)
56 +inf 0 +inf 0.0 1 385
57 +inf 2 +inf 0.0 1 385 cut: 32
58 +inf 2 +inf 0.0 1 385 cut: 15
59#1 22 11.119 49.459 0.2 85 386 sol: relax
60 22 22 0.000 0.6 0 386
61
62<iteration end>
63
64[Result]
65STATUS OPTIMAL
66VALUE_OF_OBJECTIVE 22
67SIMPLEX_PIVOT_COUNT 21493
68PARTIAL_PROBLEM_COUNT 7729
69ELAPSED_TIME(sec.) 0.56
70
71[Print]
721 1.0 1.0
732 0 0
743 2.0 1.0
754 0 2.0
765 3 4
776 0 3
787 4 0
798 1.0 0
引用書式