4. 巡回セールスマン問題#
4.1. 背景#
巡回セールスマン問題もしくは巡回セールスパーソン問題は, 整数計画問題の代表例としてしばしば紹介される最適化問題である. また文献ではよく Traveling Salesman Problem の頭文字から TSP と省略されることが多い.
Hamilton 閉路の中で辺の重みの総和が最小となるものを求める問題ともいえる.
Tip
Euler 閉路に置き換えた場合に相当する問題は『中国人郵便配達問題』とよばれる問題である.
4.2. 設定#
巡回セールスマン問題をグラフ理論の言葉で少し言い換えると次のとおり.
問題で扱う都市の集まり \(C\) を頂点集合とし, 各都市間の可能な経路の集まりを辺集合 \(E=\{(c_1,c_2)\}\) とするとき, グラフ \(G=(C,E)\) の上で最短閉路を求めるが,巡回セールスマン問題である.
注意
\((c,c)\) に対応する経路 \(c\to c\) は二度同じ都市を訪問することから, 巡回セールスマン問題を扱う際には考えないこととする.
Tip
巡回セールスマン問題には亜種として関連付けられるいくつかの問題がある. 代表的なものとしては次がある.
- TSP 経路問題
出発地点と到着地点を別々にとり,すべての都市を巡るが元に戻ってこない場合で,最短経路を求める問題
- 最短経路問題
出発地点と到着地点を別々にとり,最短経路を求める問題
4.2.1. Hamilton 閉路とは#
頂点集合 \(V\),辺集合 \(E\) についてのグラフ \(G=(V,E)\) 上の閉路を考えるとき, グラフ理論では次の二つの閉路が計算量の観点からよく比較対象にされる.
- Euler 閉路
すべての 辺 を一回だけ通って,最初の頂点に戻ってくる閉路
- Hamilton 閉路
すべての 頂点 を一回だけ通って,最初の頂点に戻ってくる閉路
4.2.1.1. 例 (Euler 閉路)#
図 4.1 は Euler 閉路になっている.
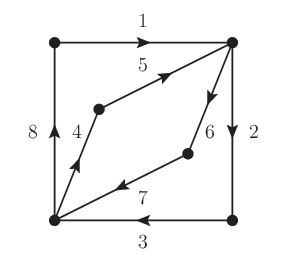
図 4.1 各辺に Euler 閉路を巡回する際の番号を一例として付している.#
図 4.2 は Euler 閉路ではない.
図 4.2 Königsberg の橋#
4.2.1.2. 例 (Hamilton 閉路)#
図 4.3 は Hamilton 閉路になっている.
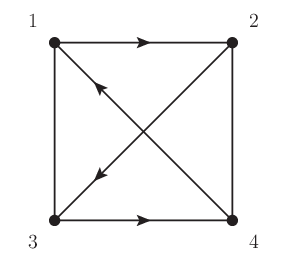
図 4.3 各頂点に Hamilton 閉路を巡回する際の番号を一例として付している.#
図 4.4 は Hamilton 閉路ではない.
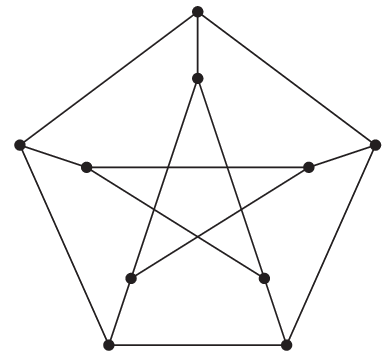
図 4.4 Petersen グラフは Hamilton 閉路を持たない.#
4.2.2. 計算効率#
与えられたグラフが Euler 閉路であることを証明することは易しい問題であり, 一方で Hamilton 閉路であることを証明することは難しい問題である.
与えられた (連結な) グラフについて,各頂点に属する辺の数が偶数個であるかどうか判定できれば, Euler 閉路かどうか必要十分に決定できるからである. \(|V|\) 個ある頂点について順に辺の数をみていけばよく,多項式時間で決定できる.
しかし Hamilton 閉路はそのような効率的なアルゴリズムが知られておらず, 各頂点を巡るすべてのパターンを見ていくことになる. 単純には \(|V|!\) とおりだけあって,非効率的である.
Tip
任意のグラフではなく,一部の特別な条件を満たす場合には Hamilton 閉路であることを効率的に判定できることはよく知られている. それらは Dirac の定理,Ore の定理などである.
なお Dirac は物理学者の P.A.M. Dirac ではなく,数学者の Gabriel Andrew Dirac のことである. https://en.wikipedia.org/wiki/Gabriel_Andrew_Dirac
巡回セールスマン問題は特別な Hamilton 閉路を求める問題であり, これもまた効率的なアルゴリズムは知られていない.
これらの問題に対して効率的なアルゴリズムが見つかれば, 他の類似した非効率的な問題も効率的に解けることになる. つまりそれだけ効率的なアルゴリズムを見つけることは難しい問題であり, 見つけた者は大いなる栄誉の頂に立てる [1].
4.3. 読み取り#
巡回セールスマン問題を数理最適化問題として定式化しよう. 数理最適化の文脈で巡回セールスマン問題を扱う場合には, 厳密解法だけでなく近似解法への切り替えも比較的シームレスに検討できる.
巡回セールスマン問題の定式化はいろいろな工夫を凝らすことができるという点でも教育的な題材である. それでは見ていこう.
4.3.1. 二次最適化#
- 変数 \(x_{c,n}\)
都市 \(c\) を \(n\) 番目に巡回する場合に \(1\) をとり,そうでない場合に \(0\) をとるものとする.
(2)#\[x_{c,n}\in\mathbb{B}, \, \forall c\in C, \forall n\in \{1,\cdots,N\}\]- 目的関数 \(TotalDistance\)
- (3)#\[TotalDistance = \sum_{c_1,c_2}\sum_{n=1}^N D_{c_1,c_2} x_{c_1,n} x_{c_2,n+1}\]
- 制約条件
注釈
上記に述べた定式化は QUBO 形式としても定式化を転用することもできる.
4.3.2. MILP#
先の定式化は目的関数が二次になる場合だった. 変数を次のように変更することで,MILP として定式化できることを次に見る.
- 変数 \(x_{c_1,c_2}\)
都市間 \((c_1,c_2)\) を移動する場合に \(1\),そうでない場合に \(0\) をとるものとする.
(6)#\[x_{c_1,c_2}\in\mathbb{B}, \, \forall (c_1,c_2)\in E\]- 中間変数 \(y_c\)
都市 \(s\) を出発してから,何番目に都市 \(c\) を訪問するか.
(7)#\[y_c\in\mathbb{R}, \, \forall c\in C\setminus\{s\}\]- 目的関数 \(TotalDistance\)
- (8)#\[TotalDistance = \sum_{(c_1,c_2)\in E} D_{c_1,c_2} x_{c_1,c_2}\]
- 制約条件
閉路条件
サブツアー禁止条件
上記の制約条件について個別に言及する. 特に中間変数についてはサブツアー禁止条件とともに詳しく解説する.
4.3.2.1. 閉路条件#
都市を表す各頂点で入次数と出次数とが共に \(1\) であれば, 何らかの閉路を定めることができる. これをここでは閉路条件とよぶことにすれば, この条件は次の二つの制約条件式として記述できる.
4.3.2.2. サブツアー禁止条件#
閉路条件だけだとすべての都市を巡らない閉路が複数選択されうる. 実際,\(x_{c_1,c_2}=x_{c_2,c_1}=1\) で閉路条件が満たされるが, これは二つの都市間だけで閉じた部分的な閉路 \(c_1\to c_2\to c_1\) になっている. このように部分的な都市 (頂点) のみを訪問する閉路のことをサブツアーとよぶ.
サブツアーを禁止するための制約条件として次を考える [2].
ここで \(s\) とは出発する最初の都市のことである. そして \(y_c\) は新たに追加した連続な中間変数 1最適解を直接に与えないという意味で,そのような変数のことを中間変数という. であり,その意味は後述する.
このような制約条件 (10) を連立することで,任意のサブツアーが禁止されている.
例えば \(s\) を除くすべての都市について閉路を考えることが可能な場合に, 仮に \(s=c_N\) とすると,\(c_1\to c_2\to \cdots\to c_{N-1}\to c_1\) というサブツアーが選択されうる. ところが (10) のうち,特に次に着目しよう.
するとこれらをすべて辺々足し上げて,次の制約条件が得られる.
左辺は \(N-1\) 項だけあるから, \(c_1\to c_2\to \cdots\to c_{N-1}\to c_1\) というサブツアーに対応する次の解は, この制約条件を満たすことができない.
つまりサブツアーは禁止されている. このことは他のどのサブツアーについても,同様にして禁止されていることを示すことができる.
4.3.2.3. 中間変数 \(y\) について#
サブツアー禁止条件に含まれる中間変数 \(y\) は,訪れる都市の順番として解釈できる. このことを次に説明しよう.そのために出発する都市 \(s\) に対して \(C_s = C\setminus \{s\}\) を定義しておく.
サブツアー禁止条件 (10) は \(y\) の差分となっているので, すべての \(y_c\) について次のように定数値 \(A\) だけずらして再定義したとしても,同一の制約条件式 (10) を与える.
このことから中間変数 \(y\) は原点の取り方に任意性があるとわかる.
次に差分の上下限が次のように評価できる. まずサブツアー禁止条件条件 (10) について, \(x_{c_1,c_2}=0\) の場合を考えて,\(y_{c_1}-y_{c_2}\leq N-2\) が得られる. 同様に \(x_{c_2,c_1}=1\) の場合を考えて,\(y_{c_1}-y_{c_2}\geq 1\) が得られる. つまり差分の上下限として次が得られた.
ここで特に次が成立しているともいえる.
これらのことは \(N-1\) 個ある中間変数 \(y\) が定義域は実数集合ではあるものの, 適切に定義域を縮小すれば,制約条件を満たすためには \(1\) ずつ階段状に値が並ぶことを述べている.
何故ならば,今,出発都市 \(s\) について \(s\to c_1\to\cdots\to c_{N-1}\to s\) といった閉路が解として存在したとしよう. すると経路 \(c_1\to\cdots\to c_{N-1}\) について,\(x_{c_1,c_2}=\cdots=x_{c_{N-2},c_{N-1}}=1\) であるから, サブツアー禁止条件 (10) より次が従う.
すると各変数は一つ前の変数よりも \(1\) 以上大きくなければならない. ここで次のように各変数について上下限制約を与えて,定義域を縮小する.
この範囲に絞ると,\(y_{c_{\max}} - y_{c_{\min}} = y_{c_{N-1}} - y_1 \leq N-2\) なので, \(y_1=1\) と下限値の値をとったとしても,\(y_{c_{N-1}}\leq N-1\) と押さえられることになる. そして一方でこのとき,(18) から \(y_{c_k}\geq k\) が従う. これらのことは \(y_{c_{N-1}}=N-1\) を導き,続けて \(y_{c_{N-2}}=N-2,\cdots,y_{c_2}=2\) が従うからである.
以上のようにして中間変数 \(y\) の定義域を定めるとき,実行可能解に対して, 各 \(y_c\) は都市 \(c\) を何番目に訪問したかを表す正整数値の値をとることがわかる.
4.4. 求解#
図 4.5 に示す都市および都市間距離について,それぞれの定式化について求解する.
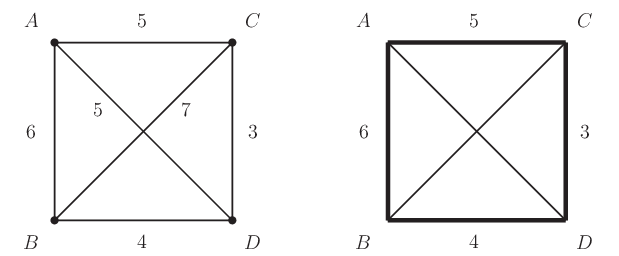
図 4.5 左図に都市 A,B,C,D および辺にそれら都市間の距離を記した.右図は太線で最短閉路を記しており,その最適値である最短距離は \(18\) である.都市間の往路と復路がそれぞれすべて同一距離ならば,一つの最短閉路に対して時計回りと反時計回りの二つの順路がある.この場合,最適解ではそれらの何れかが算出される.#
4.4.1. 二次最適化#
あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる.
PySIMPLE Sample Code
1def optimize(data):
2 from pysimple import Problem, Set, Element, BinaryVariable, Parameter, Sum, Printf
3
4 p = Problem(name='TSP', type=min)
5
6 EDGES = Set(value=data.keys()) # 都市間経路集合
7 C = EDGES(0) # 都市集合
8 c = Element(set=C)
9 c1 = Element(set=C)
10 c2 = Element(set=C)
11 c1c2 = c1!=c2
12 D = Parameter(index=c1c2, value=data)
13
14 N = len(c.set)
15 n = Element(value=range(1,N+1));
16 n_ = Element(value=range(1,N));
17
18 x = BinaryVariable(index=(c,n))
19 p += Sum(D[c1c2]*x[c1c2(0),n_]*x[c1c2(1),n_+1]) + Sum(D[c1c2]*x[c1c2(0),N]*x[c1c2(1),1]), 'TotalDistance'
20 p += Sum(x[c,n], n) == 1
21 p += Sum(x[c,n], c) == 1
22
23 p.options.method = 'wcsp' # 'wls'
24 p.solve(silent=True)
25 print(p.objective.val)
26 print(x[x[c,n].val==1].val)
27
28data = {
29 ('A', 'B'): 6, ('A', 'C'): 5, ('A', 'D'): 5,
30 ('B', 'A'): 6, ('B', 'C'): 7, ('B', 'D'): 4,
31 ('C', 'A'): 5, ('C', 'B'): 7, ('C', 'D'): 3,
32 ('D', 'A'): 5, ('D', 'B'): 4, ('D', 'C'): 3
33}
34optimize(data)
上記を実行すると次の結果を得る.
Result
1TotalDistance.val=18
2x[A,3].val=1
3x[B,4].val=1
4x[C,2].val=1
5x[D,1].val=1
4.4.2. MILP#
あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる. 求める経路は閉路であるから,出発する都市はどの都市でもよい. ここでは都市 A としている.
PySIMPLE Sample Code
1def optimize(data):
2 from pysimple import Problem, Set, Element, BinaryVariable, Variable, Parameter, Sum, Printf
3
4 p = Problem(name='TSP', type=min)
5
6 # 集合・添字
7 EDGES = Set(value=data.keys()) # 都市間経路集合
8 C = EDGES(0) # 都市集合
9 c = Element(set=C)
10 c1 = Element(set=C)
11 c2 = Element(set=C)
12
13 c_ = c != c.set[0] # 出発地点を除く都市
14 c1_ = Element(set=c_.set)
15 c2_ = Element(set=c_.set)
16
17 # 定数・変数
18 c1c2 = c1!=c2
19 N = len(c.set)
20 D = Parameter(index=c1c2, value=data)
21 x = BinaryVariable(index=c1c2)
22 y = Variable(index=c_, lb=1, ub=N-1)
23
24 # 目的関数
25 p += Sum(D[c1c2]*x[c1c2]), 'TotalDistance'
26
27 # 閉路条件
28 p += Sum(x[c1c2], c1c2(0)) == 1
29 p += Sum(x[c1c2], c1c2(1)) == 1
30
31 # サブツアー禁止条件
32 c1c2_ = c1_!=c2_
33 p += y[c1c2_(0)] - y[c1c2_(1)] + (N-1)*x[c1c2_] <= N-2
34
35 # 求解
36 p.solve(silent=True)
37
38 # 出力
39 print(p.objective.val)
40 print(x[x[c1c2].val==1].val)
41 Printf('都市 {} の訪問順位: {:f}', c_, y[c_].val)
42
43data = {
44 ('A', 'B'): 6, ('A', 'C'): 5, ('A', 'D'): 5,
45 ('B', 'A'): 6, ('B', 'C'): 7, ('B', 'D'): 4,
46 ('C', 'A'): 5, ('C', 'B'): 7, ('C', 'D'): 3,
47 ('D', 'A'): 5, ('D', 'B'): 4, ('D', 'C'): 3
48}
49optimize(data)
上記を実行すると次の結果を得る.
Result
1TotalDistance.val=18
2x[A,B].val=1
3x[B,D].val=1
4x[C,A].val=1
5x[D,C].val=1
6都市 B の訪問順位: 1.000000
7都市 C の訪問順位: 3.000000
8都市 D の訪問順位: 2.000000
技法集
参考文献
ランス・フォートナウ. P≠NP予想とはなんだろう ゴールデンチケットは見つかるか? 日本評論社, 2014. ISBN 978-4-535-78728-5. URL: https://www.nippyo.co.jp/shop/book/6524.html.
H.P.ウイリアムス. 数理計画モデルの作成法. 産業図書, 1995.
Robert Bosch. Opt Art: From Mathematical Optimization to Visual Design. Princeton Univ Press, 2019. URL: https://press.princeton.edu/books/hardcover/9780691164069/opt-art.
引用書式
BibTeX
