2. 輸送問題#
2.1. 背景#
輸送問題とは「複数の供給地」から「複数の需要地」への「物の流れ方」を決める問題ということができる. 供給地と需要地をノード,物の流れる経路をアークとすれば,輸送問題はネットワークによって表現できる問題の一種と捉えることができる. そして輸送問題に対する定式化の方法は他のネットワークによって表現できる問題にも応用できる.
2.2. 設定#
2.3. 集合および定数#
「工場の集まり」と「店舗の集まり」が,与えられた設定での集合となっている. これらが「供給可能量」「需要量」という定量的なデータを個々に定めるからである.
数式としては「工場の集まり」と「店舗の集まり」をまず集合として立式できる.
続いてこれらに紐づく定数として「供給可能量」「需要量」が立式できる.
以上を PySIMPLE で記述すると次のようになる.
1from pysimple import Set, Element, Parameter
2FACTORIES = Set(dim=1, value=[1,2])
3f = Element(set=FACTORIES)
4SHOPS = Set(dim=1, value=['a','b','c'])
5s = Element(set=SHOPS)
6UPPER_SUPPLY = Parameter(index=f, value={
7 1: 250,
8 2: 450
9})
10DEMAND = Parameter(index=s, value={
11 'a': 200,
12 'b': 200,
13 'c': 200
14})
2.4. 変数#
定数の傾向から変数を設計していく.
各工場には供給可能量とよぶところの生産量に関する上限値が与えられている. これから工場 \(f\) の生産量は \(0\) から \(UPPER\_SUPPLY[f]\) の自由度があると考えてよいだろう.
そして生産する製品の種類が特に指定されていないから,製品の種類の自由度はなく, ある一つの品目についての生産だということが仮定されていると読み取れる. その一つの品目を店舗 \(s\) が \(DEMAND[s]\) だけ欲していることになる.
このことから工場 \(f\) ではどれだけの量を店舗 \(s\) のために生産すればよいかという輸送量 \(x\) を決定すればよいとわかる. つまり変数としては次を考えればよく,また図に示すネットワークを考えればよい.
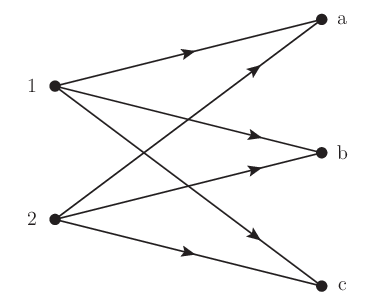
図 2.1 輸送問題の定式化に対応するネットワーク#
ここで,この変数が実変数であることを今暗黙に仮定したが,厳密に実数の自由度を有しているとは言い難い. 工場で生産できる最小ロットのようなものを想定する方がより現実的であり, これを単位として供給可能量や需要量が入力データとして与えられることは不思議なことではない.
よって \(x[f,s]\in\mathbb{Z}\) と整数変数とすべきだろうか.
もちろん,そのようにしてもよいが,求解難易度は上昇することになる. これらの違いをまとめると次のようなものである.
観点 |
実変数の場合 |
整数変数の場合 |
|---|---|---|
求解難易度 |
減少 |
上昇 |
現実忠実度合 |
中 |
大 |
後処理 |
有 |
無 |
どちらが良いかは実要件に強く依存して変わるのだが,以下,我々は実変数だとする.
以上を PySIMPLE で記述すると次のようになる.
1# case: x in Real Numbers
2from pysimple import Variable
3x = Variable(index=(f,s))
4
5# case: x in Integer Numbers
6from pysimple import IntegerVariable
7x = IntegerVariable(index=(f,s))
2.5. 制約条件#
変数が立式できると,変数の上下限制約という観点で制約条件を明らかにできる. 今回の変数は \(x[f,s]\) で各添字 \(f\) (工場) と \(s\) (店舗) それぞれについての上下限制約にどのようなものがあるかを考える.
2.5.1. 生産量の上下限制約#
各工場での生産量の限界が供給可能量として与えられていたので,次式が思い浮かんだとしよう.
この中辺と右辺は店舗数が \(1\) でない限り正しくない. 複数店舗ある場合に,どの店舗についても供給可能量することを許容していることになるからである. 今の場合には次のように,すべての店舗への供給を考慮して足し上げた量について上限と比較する必要がある.
こうして改良したが,すると今度は左辺と中辺が複数店舗の場合に正しくなくなってしまう. 足し上げる量の中に負値があっても,総和で非負であればよく,\(x\) が負値となる場合が許容されるからである.
これを避けるために生産量の上限とは別に次の非負制約を課す.
この非負制約を課すことで,生産量の上限制約は次のようになる.
以上のように変数 \(x\) の上下限制約を与える不等式は,\(L\leq x\leq U\) というように続けて書かずに, \(x\geq L\) そして \(x\leq U\) と分離して整理していくと間違いを犯しにくい. 加えてより複雑な式変形をしていく中では,予め分けて書いて置く方が修正がしやすい. この他,個別の要件として制約条件式を分けて記述できるため,保守という点でもロバストな記述といえる.
これまでの議論に対する PySIMPLE の記述は次のようになる.
1from pysimple import Problem, Sum
2problem = Problem(name='transportation-problem')
3problem += x[f,s] >= 0, 'CoNonNegativity'
4problem += Sum(x[f,s], s) <= UPPER_SUPPLY[f], 'CoUpperSupply'
2.5.2. 需要量の上下限制約#
各店舗での需要量は輸送量 \(x\) の下限値を与えていると考えることができる. 生産量の上限制約と同様に考えて,この下限制約は次のように立式できる.
等号成立の場合は需要丁度で過剰供給がない場合である. 問題設定からは過剰供給については何等の言明がないため,ここでは忠実に過剰供給の場合を許容した立式になっている.
しかし現実には過剰供給はどちらかと言えば (在庫を抱えることになるため) 歓迎されない. よって次のように等式制約として記述すべきである.
等式制約に関して PySIMPLE の記述は次のようになる.
1problem += Sum(x[f,s], f) == DEMAND[s], 'CoDemand'
注釈
より発展的な話題としては非負値のスラック変数 \(slk\) を導入して目的関数に含めてもよいだろう.
このスラック変数は在庫量としての意味を担わせることができる. ただ目的関数を \(x\) について正係数の線形な関数として記述して最小化を図る場合には, 変数 \(x\) 自体が小さいほど最適なので,このスラック変数の必要性は薄れる. 不等式制約であっても \(x\) 自体が可能な限り \(DEMAND\) に張り付こうとするからである.
需要量の下限制約は何も生産しないことが最適とはならないための制約条件ともいえる. このことからスラック変数としては次式のように,生産量がどれだけ貧弱かを評価する不足量として立式する方がより現実的である.
2.6. 目的関数#
「もっともコストがかからない製品の運び方」というものを表現したい. 問題設定からはコスト関数がどのように算定されるものかは明示されていない.
変数として輸送量を考えているから,この輸送量に依存した形でコスト関数が与えられると考えられる. 現実世界を考えると輸送量には様々な要因が含まれており,コスト関数は非線形関数だと考えられる. しかし非線形性の度合いがよほど強くはない限りは,そのような厳密な定式化は筋が悪い.
このような背景からコスト関数としては輸送量に線形な関数と仮定して定式化を図る.
ここでコスト係数 \(COST[f,s]\) は工場 \(f\) から店舗 \(s\) への輸送量の単位量あたりの輸送コストである. まとめると目的関数の定式化で重要な点は次の二点である.
目的関数は線形であること.
線形性を仮定するために必要な入力データを用意すること.
以上を PySIMPLE で記述すると次のようになる.
1COST = Parameter(index=(f,s), value={
2 (1,'a'): 3.4,
3 (1,'b'): 2.2,
4 (1,'c'): 2.9,
5 (2,'a'): 3.4,
6 (2,'b'): 2.4,
7 (2,'c'): 2.5
8})
9problem += Sum(COST[f,s]*x[f,s]), 'TotalCost'
2.7. 求解#
あらためて定式化と対応する PySIMPLE をすべて書き出すと次のようになる.
PySIMPLE Sample Code
1from pysimple import Problem, Set, Element, Parameter, Variable, Sum
2
3def optimize(method):
4 # Sets and Parameters
5 FACTORIES = Set(dim=1, value=[1,2])
6 f = Element(set=FACTORIES)
7 SHOPS = Set(dim=1, value=['a','b','c'])
8 s = Element(set=SHOPS)
9 UPPER_SUPPLY = Parameter(index=f, value={
10 1: 250,
11 2: 450
12 })
13 DEMAND = Parameter(index=s, value={
14 'a': 200,
15 'b': 200,
16 'c': 200
17 })
18
19 # Variables
20 x = Variable(index=(f,s))
21
22 # Constraints
23 problem = Problem(name='transportation-problem')
24 problem += x[f,s] >= 0, 'CoNonNegativity'
25 problem += Sum(x[f,s], s) <= UPPER_SUPPLY[f], 'CoUpperSupply'
26 problem += Sum(x[f,s], f) == DEMAND[s], 'CoDemand'
27
28 # Objective
29 COST = Parameter(index=(f,s), value={
30 (1,'a'): 3.4,
31 (1,'b'): 2.2,
32 (1,'c'): 2.9,
33 (2,'a'): 3.4,
34 (2,'b'): 2.4,
35 (2,'c'): 2.5
36 })
37 problem += Sum(COST[f,s]*x[f,s]), 'TotalCost'
38
39 # Solve
40 problem.options.method = method
41 problem.solve()
42
43 # Print
44 print('\n[Print]')
45 print(x.val)
46
47optimize('higher')
上記を実行すると次の結果を得る.
Result
1
2[About Nuorium Optimizer]
3Nuorium Optimizer 24.1.0 build:614ca4b
4 <with META-HEURISTICS engine "wcsp"/"rcpsp">
5 <with Netlib BLAS>
6, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
7
8[Problem and Algorithm]
9PROBLEM_NAME transportation-problem
10NUMBER_OF_VARIABLES 6
11NUMBER_OF_FUNCTIONS 12
12PROBLEM_TYPE MINIMIZATION
13METHOD HIGHER_ORDER
14
15[Progress]
16<preprocess begin>.........<preprocess end>
17<iteration begin>
18 res=2.3e+01 .... 4.5e-05 4.4e-07
19<iteration end>
20
21[Result]
22STATUS OPTIMAL
23VALUE_OF_OBJECTIVE 1620.000001
24ITERATION_COUNT 6
25FUNC_EVAL_COUNT 9
26FACTORIZATION_COUNT 7
27RESIDUAL 4.424713473e-07
28CONSTRAINT_INFEASIBILITY 5.684341886e-14
29ELAPSED_TIME(sec.) 0.00
30
31[Print]
32x[1,a].val=29.56597420813169
33x[1,b].val=199.99999778761767
34x[1,c].val=1.1061694962526445e-06
35x[2,a].val=170.43402579186832
36x[2,b].val=2.2123823790951827e-06
37x[2,c].val=199.99999889383054
この結果は STATUS が OPTIMAL より最適解となっているのだが,小数点以下の端数がたくさん出ている.
これは使用した求解アルゴリズムが (線形計画専用) 内点法であるため,数値的な収束半径に入って計算が停止したことを示唆している.
例えば x[1,c] や x[2,b] は厳密に \(0\) である可能性が高い.
そこで次のように単体法を指定して求解してみる.
1optimize('simplex')
すると次の求解結果を得る.
Result
1
2[About Nuorium Optimizer]
3Nuorium Optimizer 24.1.0 build:614ca4b
4 <with META-HEURISTICS engine "wcsp"/"rcpsp">
5 <with Netlib BLAS>
6, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
7
8[Problem and Algorithm]
9PROBLEM_NAME transportation-problem
10NUMBER_OF_VARIABLES 6
11NUMBER_OF_FUNCTIONS 12
12PROBLEM_TYPE MINIMIZATION
13METHOD SIMPLEX
14
15[Progress]
16<preprocess begin>.........<preprocess end>
17<iteration begin>
18
19 .12
20
21
22<iteration end>
23
24[Result]
25STATUS OPTIMAL
26VALUE_OF_OBJECTIVE 1620
27SIMPLEX_PIVOT_COUNT 5
28RESIDUAL 0.05952380952
29ELAPSED_TIME(sec.) 0.00
30
31[Print]
32x[1,a].val=50.0
33x[1,b].val=200.0
34x[1,c].val=0.0
35x[2,a].val=150.0
36x[2,b].val=0.0
37x[2,c].val=200.0
これは再び最適解であり,得られた解には端数がなくなっている.
引用書式
