Ctrl+K

線形な定式化とネットワーク

1. 線形な定式化とネットワーク#

1.1. 背景#

線形な定式化は現実的な計算資源と実務規模での問題を求解するという点で， 何よりも最初に検討すべき定式化である．

様々な分野の問題解決を数理最適化の文脈で行うことができるが， この場合にどのように考えることで線形な定式化の範囲とできるか， もしくはそういった線形な定式化の特徴をどのように見出せばよいのか， といったことを様々な定式化事例を通して見ていく．

一つの重要な特徴はネットワークとしての解釈を線形な定式化に見出せる点であり， 様々な事例の言及に先立ってこの観点を述べることには大変な意義がある． 下図はこの重要な特徴を模式的に表したものである．

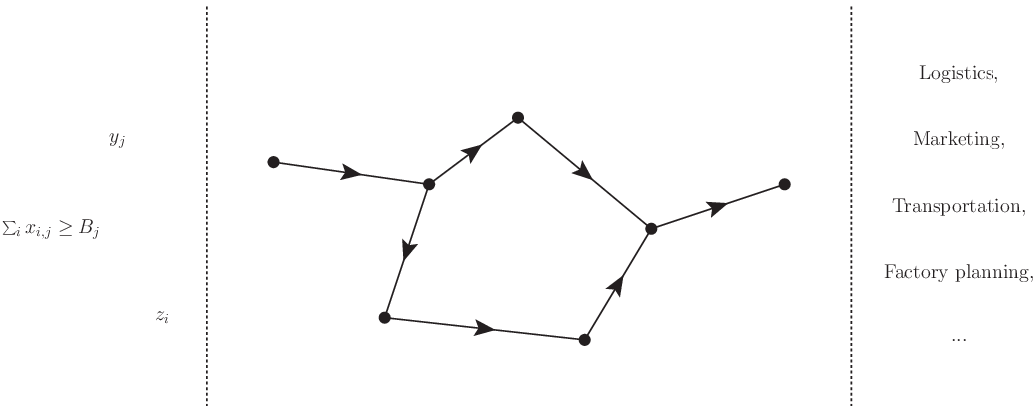
応用分野と定式化を結び付けるネットワーク概念

図 1.1 応用分野と定式化を結び付けるネットワーク概念#

図の中央がネットワークとよぶもので，頂点と辺からなっている． その右側にこのネットワークとして抽象化しようとした様々な応用分野が紐づいている． 図の左側は最も抽象化された層で，我々が数理最適化とよぶところの変数や制約条件，そして目的関数に相当する数式の集まりである．

つまりこの図からわかることは，数理最適化の定式化を行う専門家や実務家は， この抽象化(もしくは具象化)の濃淡を図のように捉えている側面があるということである．

ネットワークはちょうど中間程度の抽象度であり， 数式と実務を結び付ける思考モデルの一つとして汎用性の高い概念もしくはツールになっている．

我々が線形な定式化を考える場合に図の最も左側には， 線形最適化問題の標準形が一般にはくる． それが最初の具象化の段階として，どのようなネットワークに対応するのかが重要となる． これを以下に整理しまとめる．

1.2. ネットワークとフロー#

ネットワークとは重み付き有向グラフとよぶものであり，それは次の特徴を持つ構造である．

  • 頂点 \(v\) の集合 \(V\) と辺 \(e\) の集合 \(E\) からなるグラフ \(G=(V,E)\) である．

  • 辺 \(e=(v_i,v_j)\) には頂点 \(v_i\) から \(v_j\) に向かう向きがあり，その向きを図示する場合には矢の向きで図示する．

  • 頂点や辺には重み \(w\) とよぶ数を割り当てることができる．

ネットワークの定義から電気回路図や制御工学でのブロック線図， 化学プラントでのプロセスフロー図など， もしくはもっと身近な例として鉄道の路線図のように， 様々な具体例を見出すことができる．

数理最適化では以下の対応を見出す． 但し主たる一例であって，必ずしもこのような対応を考えなければならないということは意味しない．

数理最適化

ネットワーク

集合

頂点集合や辺集合

定数

重み

変数

フロー

制約条件

フロー間の条件

目的関数

重みとフローの総量

ここで「フロー」というものが重要であり， フローとは重みを変数として捉えた場合をいう．

ネットワーク上を流れる何某かの流量をフローは意味し， この流量を調節することで流れを最適化しようというのがネットワーク上の表現となる．

1.3. 変数#

ネットワーク上の変数 \(x\) とはフローであり，辺 \(e=(i,j)\) で添字付けられる．

(1)#\[x_{(i,j)} \in \mathbb{R}\]

この他にも何かしらネットワークの構造に関連した変数を適宜定めることができるが， それは問題に応じて必要に応じて追加するものであり，問題のコアとなる構造にフローがないかどうかを考えることになる．

変数 \(x_{(i,j)}\) を構築したら，これからネットワーク上の次の基本的な中間変数を定義できる．

(2)#\[\begin{split}in_j &:= \sum_{i\in I} x_{(i,j)}, \\ out_j &:= \sum_{k\in K} x_{(j,k)}\end{split}\]

\(in_j\) と \(out_j\) はそれぞれ頂点 \(j\) に流れ込むフローの総量と流れ出るフローの総量を表す． 総量の範囲は集合 \(I\) や \(K\) で与えることができる．

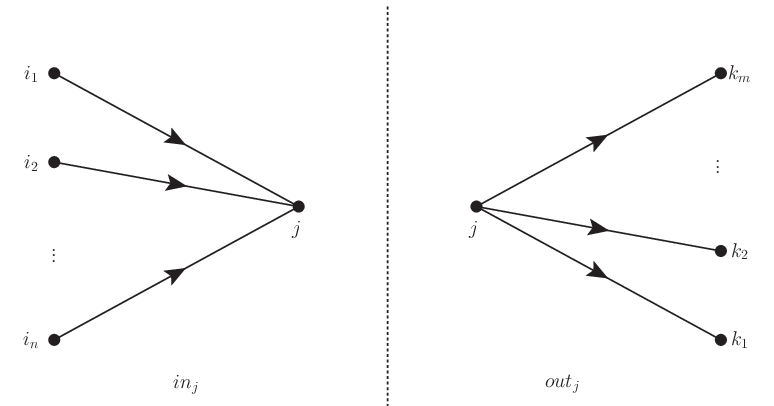
左が中間変数 :math:`in_j` を表し，右が中間変数 :math:`out_j` を表すネットワークである．

図 1.2 左が中間変数 \(in_j\) を表し，右が中間変数 \(out_j\) を表すネットワークである．#

これら中間変数を用いることで，ネットワーク上の接続を集約できる． そして次に述べる基本的な制約条件の記述に用いることができる．

1.4. 制約条件#

フローに関連する制約条件の代表例は「上下限制約」と「フロー保存則」である．

1.4.1. 上下限制約#

頂点に到達するフローの総量や辺上のフローの量が所定の上下限値を満たしているかどうかを扱うのが上下限制約である．

1.4.1.1. 頂点の場合#

(3)#\[L_j \leq in_j \leq U_j\]

この上下限制約は中辺が頂点 \(j\) へ流れ込む総量を表すため， 頂点 \(j\) での需要量の上下限制約と考えることができる．

同様に次の不等式制約は中辺が頂点 \(i\) から流れ出る総量を表すため， 頂点 \(j\) での供給量の上下限制約と考えることができる．

(4)#\[L_j \leq out_j \leq U_j\]

何れも頂点に対応させている実際の事物の能力がしばしばよく反映される．

1.4.1.2. 辺の場合#

(5)#\[L_{(i,j)} \leq x_{(i,j)} \leq U_{(i,j)}\]

この上下限制約はちょうど水道管の管の大きさが流量の上限を定め， 管の傾きが流れ出すのに要する下限を定めるようになもので， 辺に対応させている実際の事物の物理的な制約がしばしばよく反映される．

1.4.2. フロー保存則#

湧き出し (source) と吸い込み (sink) がない限り，水の流れには途切れがないように， ネットワーク上のフローの各頂点での出入りは常に一定であることがフロー保存則である．

頂点 \(j\) でのフロー保存則を書けば次の等式制約となる．

(6)#\[in_j = out_j\]

左辺は頂点 \(j\) に入ってくるフローの総量を表し， 右辺は頂点 \(j\) から出ていくフローの総量を表す． これらが等しいことがフロー保存則であったので，等式制約式として書ける．

境界条件としての湧き出しと吸い込みについては問題に応じて適切に定められることになる． ここでは例として頂点 \(j\) での湧き出し量が \(s_j\) だったとしよう． すると次の等式制約がフロー保存則となる．

(7)#\[s_j = out_j\]

考え方は先に述べたことと同じである．但しここで \(s_j\) が変数か定数かは問題に依存する． 吸い込みについても全く同様である．

さて仮にフロー保存則が成り立っていなかったら，その場合はどのような式表現になるだろうか． その場合にはフロー保存則を成り立たなくさせている漏れまで含めて， その全体で再びフロー保存則を考えればよい．

例えば頂点 \(j\) に入ってきたフローの一部がネットワーク上から \(a_j(\geq 0)\) だけ漏れ出る場合には，次の等式制約となる．

(8)#\[in_j = out_j + a_j\]

一方で漏れではなくネットワーク上からの寄与ではない水増しが \(b_j(\geq 0)\) だけ発生する場合は次の等式制約となる．

(9)#\[in_j + b_j = out_j\]

再び \(a_j\) や \(b_j\) が変数か定数どうかは問題に依存する．

注釈

ところで仮に変数とするならば，どのような問題立てがあるのか，またはその場合にはどのようなことを想定するのか， といったことを思い描いておくことは暗黙によくなされる．

例えばオペレーション上，漏れや水増しが本来はあって欲しくないが，これらが何かの理由で存在し得る場合を想定するのならば， これら変数を (非負条件は課すとして) 目的関数として最小化すればよい．というようなことを考えるものである． このような変数は場合によっては積極的にスラック変数としての役割を見出すこともできる．

以上のようにネットワークという中間的な抽象モデルを数理最適化という抽象的な定式化技法と結び付けて， 実務問題の構造化を図ることが大切になる．

1.5. 目的関数#

線形な定式化を大前提に考えているので，目的関数は次の形をしているものが対象となる． 以下，最小化を前提とする．

(10)#\[\sum_{(i,j)} ECOST_{(i,j)}\cdot x_{(i,j)}\]

\(ECOST_{(i,j)}\) は辺 \((i,j)\) に割り当てられた重みであり，最小化すべきコストをここでは意味する．

一方で頂点 \(i\) に関する重み \(VCOST_i\) を最小化すべきコストとして考える場合には， 問題に応じて適切な境界条件を設けたネットワークの設定の下で線形に定式化することになるが，ここでは省略する．

1.6. 式とネットワークの対応#

ここまではどちらかと言えばネットワークを前提に，線形な定式化はどのようになるかを見てきたが， 逆に式の形を前提にどのようなネットワークが対応するかを考えることもできる． その対応はこれまでの振り返りとなるが次のとおりである．

式

ネットワーク

\(x_{i}\)

頂点 \(i\) (または一端が固定された辺)

\(x_{(i,j)}\)

辺 \((i,j)\)

\(x_{(i,i)}\)

頂点 \(i\) のループ

\(\sum_{i\in I} x_{(i,j)}\)

集合 \(I\) に属する頂点から流れ出て頂点 \(j\) へ流れ込むフロー総量

\(\sum_{k\in K} x_{(j,k)}\)

集合 \(K\) に属する頂点へ流れ込む頂点 \(j\) から流れ出るフロー総量

これら表では変数に対する演算は加法しか表れていないため，線形な定式化に限定されている．

つまり 目的関数の線形性はネットワークの式構造とは独立だ といえる． コストとして計上される重みがフロー単位量当たりのコストの単位を持っているため， 暗黙に予め線形性が仮定されている だけに過ぎない． それ故にネットワークとしての問題構造を見出す以前に，目的関数が線形かどうか， もしくは近似可能かを見極めておく必要がある．

Tip

仮に目的関数 \(f\) が非線形になる場合には変数 \(x\) の関数として考えれば， \(x\) がフローを表していることから，流量の規模に応じてコストが変化することを暗示している． もしくはフロー同士の和がフロー全体の和とはならない非線形量を扱う必要があることも想定される．

例えばフローが貨物の重量を表す場合に，複数の貨物の重量の合計が貨物全体の重量になるのは当然のことだが， 貨物の量が多い場合には無視できない梱包のための重量を加味しなければならないかもしれない． このような場合にはこれまで無視していたものまで含めた意味で，全体の重量として算定する必要がある． そうなると単純に足し上げることができなくなってしまう．

線形な定式化はある種の理想化がなされており，この理想化は扱う規模が大きくなるか詳細さを徹底するに従って成立しなくなっていく． この傾向は線形モデルの宿命でもある．問題の分割を図ったりヒューリスティックスに切り替えるなど， どこまでを計算側が請け負うかをよく協議しておくことが重要である．

引用書式

BibTeX

目次