6. 列生成法という技法 #

6.1. 導入 #

最適化問題の計算量は概ね，変数や制約式の数で評価でき，なるべくこれらが高々多項式程度のサイズであることが望ましい．

もしそうではない大規模な線形最適化問題を解く際，列生成法 (column generation method) [1, 2] とよばれる問題規模に伴う計算量を抑えるための手法が適用可能かどうか検討される．列生成法の説明には線形最適化問題の双対性の概念も必要であり，専門性の高い手法ともいえる．

注釈

全文を閲覧するには以下の URL にアクセスしてください: こちらのリンク

6.2. 列生成法と双対問題 #

列生成法は与えられた線形最適化問題の中で，冗長と考えられる変数または制約条件を間引くよう計算の複雑さを低減する手法である．そして本手法は主問題と双対問題との間の次の関係に着目するものである．

主問題 (Primal): (1)#\[\begin{split}\begin{bmatrix} . & . & . & . & . & * \\ . & . & . & . & . & * \\ . & . & . & . & . & * \\ . & . & . & . & . & * \\ . & . & . & . & . & * \end{bmatrix} \begin{bmatrix} . \\ . \\ . \\ . \\ . \\ * \end{bmatrix} = \begin{bmatrix} . \\ . \\ . \\ . \\ . \end{bmatrix}\end{split}\]
双対問題 (Dual): (2)#\[\begin{split}\begin{bmatrix} . & . & . & . & . \\ . & . & . & . & . \\ . & . & . & . & . \\ . & . & . & . & . \\ . & . & . & . & . \\ * & * & * & * & * \end{bmatrix} \begin{bmatrix} . \\ . \\ . \\ . \\ . \end{bmatrix} = \begin{bmatrix} . \\ . \\ . \\ . \\ . \\ * \end{bmatrix}\end{split}\]

これは模式的に線形最適化問題の双対構造を表したものである．つまり主問題の変数の追加 (\(*\) で表記) は，係数行列 \(A\) の列を追加することに対応し，このことは双対問題で係数行列 \(A^{\top}\) の行を追加することであり，制約条件の追加と対応している．また主問題と双対問題とでは，変数および制約条件式の総数について，次の関係があることからもわかる．

	変数の総数	制約条件式の総数
主問題	\(n\)	\(m\)
双対問題	\(m\)	\(n\)

列生成法の列とは，模式された式にあるように，「主問題の係数行列 \(A\) の列」のことである ¹ ¹「双対問題の係数行列 \(A^{\top}\) の行」の生成を強調する場合には行生成法ということがある．この場合には，制約条件式を追加して実行可能領域を削り取っているとも考えられるため，切除平面法とも関連する話題でもある．．このことからわかるように，列生成法は双対性と密接に関係している．つまり列生成法は主問題の観点から述べるときは変数の生成に着目し，また双対問題の観点であれば制約条件式の生成に着目することになる．

このため問題の変数または制約条件の数が指数的にスケールする場合，それらの何れであるかで，主問題あるいは双対問題に着目して説明することになる．

列生成法の手続きを一般的に述べることは抽象性が高く，わかりづらい．そこで少しだけ具象的に，その手続きを次に述べよう．

わかりやすさ，という意味では，双対問題に着目するとよいだろう [3]．この場合，制約条件式を視覚的に間引く必要性があることを問題の動機として納得しやすいからである．

例えば次の図 6.3 を見よう．

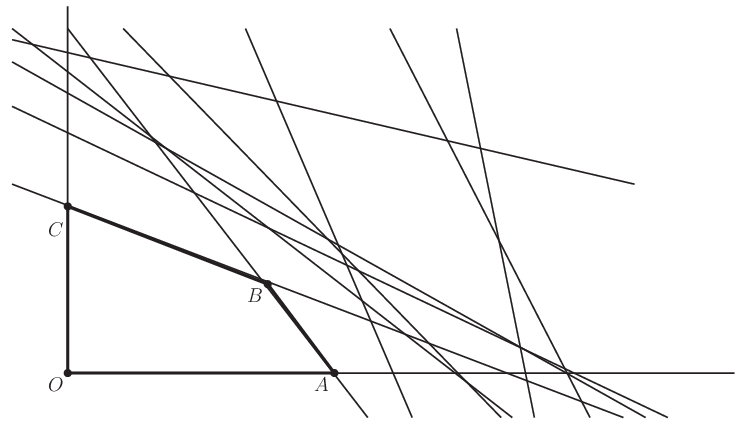
図 6.3 冗長な制約条件式が過剰にある．問題の変形に伴い，この度合が指数的にスケールしていく場合，すべての制約条件式を考慮することは効率的だとは想像できない．#

実行可能領域 \(OABC\) を真に特徴付ける制約条件式以外の式が数多くあることが見て取れる．これら制約条件式を間引き，必要な式のみを生成していこうとするのが，双対問題から見た列生成法の考え方である．

限定問題

与えられた元の問題に対して，変数や制約条件の一部を取り除いた問題のことを限定問題 (restricted problem) という．主問題であれば変数を取り除いた限定主問題，そしてこれに対応する制約条件を取り除いた双対問題を限定双対問題という．限定という用語の代わりに制限という用語を用いることもある．

6.3. 主問題から見た列生成法 #

列生成法を主問題から具体的な手続きを交えて説明しよう [4]．今，次の主問題と双対問題とに問題を整理できたとしよう．

(3)#\[\begin{split}& \mathrm{Minimize\colon}~ f(\vec{x}) = \vec{c}^{\top}\vec{x} \\ & \mathrm{subject~to\colon}~ \\ & A\vec{x} = \vec{b}, \\ &\vec{x} \geq \vec{0}\end{split}\]

(4)#\[\begin{split}& \mathrm{Maximize\colon}~ \tilde{f}(\vec{\omega}) = \vec{b}^{\top}\vec{\omega} \\ & \mathrm{subject~to\colon}~ \\ & A^{\top}\vec{\omega} \leq \vec{c}\end{split}\]

これらの問題とその最適解とをそれぞれ次の記号で書くことにする．

(5)#\[\begin{split}\vec{x}^* &= \operatorname{solve}(P(\vec{b},A,\vec{c};I,J)), \\ \vec{\omega}^* &= \operatorname{solve}(D(\vec{c},A^{\top},\vec{b};J,I))\end{split}\]

ここで \(I\) は主問題の制約条件式 \(A\vec{x} = \vec{b}\) の総数および双対問題の変数の総数を表し， \(J\) は主問題の変数の総数および双対問題の制約条件式 \(A^{\top}\vec{\omega} \leq \vec{c}\) の総数を表す．

次に主問題の変数の総数が指数的にスケールするものとして，主問題について変数の数を限定しよう．このために次の増大列 \(\{J_k\}_{k=1}^K\) を考えよう．

(6)#\[J_1 \subset J_2 \subset \cdots \subset J_K \subset J\]

この増大列の中で \(k\) 番目に着目し，次の限定主問題 \(P|_k\) とその最適解を考えよう．

(7)#\[\begin{split}P|_k &= P(\vec{b},A|_k,\vec{c}|_k,I,J_k), \\ \vec{x}_k^* &= \operatorname{solve}(P|_k)\end{split}\]

このとき次の量 \(\vec{x}_k^{\star}\) を考えよう．

(8)#\[\begin{split}(\vec{x}_k^{\star})_j = \begin{cases} (\vec{x}_k^*)_j & (j \in J_k), \\ 0 & (j \notin J_k) \end{cases}\end{split}\]

定義からこれは少なくとも元の主問題 \(P\) の実行可能解になっている．最適性が更に示されれば，\(k=K\) ということで手続きを終了できる．そうでなければ次の \(J_{k+1}\) を定義することで変数を追加して再び \(P|_{k+1}\) なる限定主問題を解いて， \(\vec{x}_{k+1}^{\star}\) を求めて，\(k=K\) となるまで続ける．

よってこの逐次的な手続きには次の決定が必要と分かる．

実行可能解 \(\vec{x}_k^{\star}\) が主問題の最適解かどうか．
最適解ではない場合に，\(J_{k+1}\) を定める方法は何か．

これらを考えるために次の限定双対問題とその最適解を考えよう．

(9)#\[\begin{split}D|_k &= D(\vec{c}|_k,A^{\top}|_k,\vec{b};J_k,I), \\ \vec{\omega}_k^* &= \operatorname{solve}(D|_k)\end{split}\]

そしてこの問題の最適解に対して，主問題 \(P\) の被約費用の最小値を考えよう．この最小値を求める問題のことを特に 価格付け問題 (pricing problem) という．

(10)#\[\min_{j\in J\setminus J_k} (\vec{\gamma})_j = \min_{j\in J\setminus J_k} \left((\vec{c})_j - \sum_{i\in I}A_{ji}(\vec{\omega}_k^*)_i\right)\]

最小値が非負，つまり各成分についてすべて非負であれば最適性条件を満たすこととなり， \(\vec{\omega}_k^*\) は元の双対問題 \(D\) の最適解でもあるとわかる．加えて双対定理から最適解 \(\vec{\omega}_k^*\) に対する双対問題 \(D\) の最適値と主問題 \(P\) (および限定主問題 \(P|_k\) の最適値) の最適値は一致する．

(11)#\[z^* = \vec{b}^{\top}\vec{\omega}_k^* = \vec{c}^{\top}\vec{x}_k^{\star} (=\vec{c}^{\top}|_k\vec{x}_k^*)\]

そうではない場合，つまり最小値が負となる場合には，次の集合 \(\bar{J}_k\) に着目する．

(12)#\[\bar{J}_k = \operatorname*{argmin}_{j\in J\setminus J_k} (\vec{\gamma})_j\]

被約費用は双対問題での制約条件違反量ともなっているので，こうして求めた集合に属している成分は最も違反している制約条件式を選び出していることになる．よって次のように \(J_{k+1}\) を定義すればよいとわかる．

(13)#\[J_{k+1} = J_k \cup \bar{J}_k\]

6.4. まとめ #

列生成法の手続きをまとめると次のとおり．

\(k=1\) とする．
主問題 \(P\) のうち，適当な数の変数を選び出し，\(J_k\) を定義する．
限定主問題 \(P|_k\) を求解して，実行可能解 \(\vec{x}_k^{\star}\) を構成する．
限定双対問題 \(D|_k\) を求解して，最適解 \(\vec{\omega}_k^*\) を求める．
最適解 \(\vec{\omega}_k^*\) に対して価格付け問題を解いて，主問題 \(P\) の被約費用が非負かどうか決定する．非負ならば \(\vec{x}_k^{\star}\) を最適解とする．負ならば \(k\to k+1\) および次式で \(J_k\) を更新する．手続き 3 へ．

(14)#\[\begin{split}\bar{J} &= \operatorname*{argmin}_{j\in J} (\vec{\gamma})_j, \\ J_k &\leftarrow J_k \cup \bar{J}\end{split}\]

列生成法の手続きの中で価格付け問題を解く部分については言明を避けていることに注意する．問題に応じて \(\vec{c}\) や \(A\) の内容を上手く設定することで，価格付け問題自体も数理最適化問題として扱うことができる．また場合によっては，近似解法を用いるなどして価格付け問題を解くことになる．つまり個別の問題構造に依存する面があるわけである．

列生成法という技法

目次

6. 列生成法という技法#

6.1. 導入#

6.2. 列生成法と双対問題#

6.3. 主問題から見た列生成法#

6.4. まとめ#

6. 列生成法という技法 #

6.1. 導入 #

6.2. 列生成法と双対問題 #

6.3. 主問題から見た列生成法 #

6.4. まとめ #