Ctrl+K

不連続な区分線形関数

4. 不連続な区分線形関数#

4.1. 導入#

折線関数の線形表現 では関数の連続性を仮定していた． 不連続な関数の場合には，以下に述べるように不連続点での跳躍の自由度を新たに考慮する必要がある．

4.2. 階段関数の定式化#

折線関数の定式化を基礎に，図 4.1 に示す多階段関数 (multi-step function) の定式化を考えてみよう．

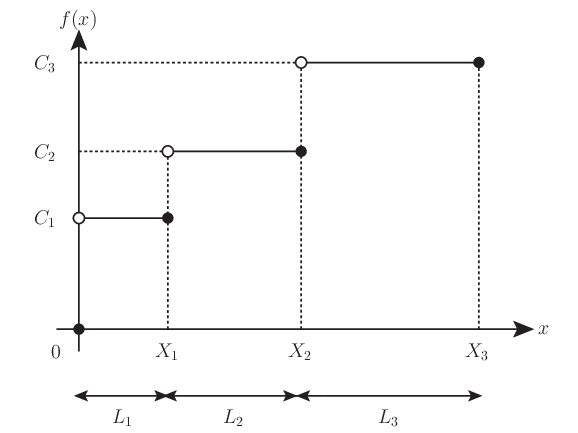
多階段関数の例

図 4.1 多階段関数の例#

定式化したい多階段関数 \(f\) の定義域は \(0\leq x\leq X_3\) であり，\(f\) の定義は式で書けば次のとおりである．

(1)#\[\begin{split}f(x) = \begin{cases} (C_0=)0 & (x=0), \\ C_1 & (X_0=0 < x \leq X_1), \\ C_2 & (X_1 < x \leq X_2), \\ C_3 & (X_2 < x \leq X_3) \end{cases}\end{split}\]

特に \(L_1=L_2=L_3=1\) と踏面の間隔が \(1\) であれば，定義域で天井関数に一致する．

(2)#\[f(x) = \lceil x\rceil ~~ (L_1=L_2=L_3=1)\]

多階段関数 \(f\) は先に与えた折線関数の定式化をそのまま使うことはできない． 区分的な定義域の境界 \(x=0,X_1,X_2\) で不連続であるため， その点でどちらの定義域を選択しているかの自由度を新たに考慮する必要があるからである．

今述べた自由度がどのように定式化に表れるのか，具体的に以下に見ていこう．

4.2.1. 基礎とする定式化#

図に示す多階段関数 \(f\) は次で与えることができる．

(3)#\[\begin{split}y = f(x) &= C_0\cdot \delta_0 + \sum_{i=1}^3 C_i\cdot \delta_i, \\ x &= X_0\cdot (\lambda_0 + \lambda_1^{\mathrm{L}}) + X_1\cdot (\lambda_1^{\mathrm{R}} + \lambda_2^{\mathrm{L}}) + X_2\cdot (\lambda_2^{\mathrm{R}} + \lambda_3^{\mathrm{L}}) + X_3\cdot \lambda_3^{\mathrm{R}}, \\ \delta_0 + \sum_{i=1}^3 \delta_i &= 1, \\ \lambda_0 &= \delta_0, \\ \lambda_i^{\mathrm{L}} + \lambda_i^{\mathrm{R}} &= \delta_i, \, \forall i\in\{1,2,3\} \\ \lambda_i^{\mathrm{L}} &\leq 1 - \varepsilon_i, \, \forall i\in\{1,2,3\}\end{split}\]

ここで定数の集まり \(\{\varepsilon_i\}_{i=1}^3\) と次の変数を定義した．

(4)#\[\begin{split}\delta_0,\delta_i &\in \mathbb{B}, \\ \lambda_0,\lambda_i^{\mathrm{L}},\lambda_i^{\mathrm{R}} &\in \mathbb{R}_{\geq0}\end{split}\]

警告

定数の集まり \(\{\varepsilon_i\}_{i=1}^3\) は small ε であり， この定式化はソルバーに負担をかける好ましくない定式化である． つまり線形な定式化が可能ではあるものの，できれば避けたいケースである．

多階段関数 \(f\) が確かに記述できていることは，次のようにして具体的に確認できる．

\(\delta_0,\delta_i \in \mathbb{B}\) および \(\delta_0 + \sum_{i=1}^3\delta_i = 1\) より， \((\delta_0,\delta_1,\delta_2,\delta_3)=(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)\) の四とおりの場合を考えればよい．

\((\delta_0,\delta_1,\delta_2,\delta_3)=(1,0,0,0)\) の場合
(5)#\[\begin{split}f(x) &= C_0 = 0, \\ x &= X_0 = 0\end{split}\]

つまりこの場合は \(f(0)=0\) に対応している．

\((\delta_0,\delta_1,\delta_2)=(0,1,0,0)\) の場合
(6)#\[\begin{split}f(x) &= C_1, \\ x &= X_0\cdot\lambda_1^{\mathrm{L}} + X_1\cdot\lambda_1^{\mathrm{R}}, \\ \lambda_1^{\mathrm{L}} + \lambda_1^{\mathrm{R}} &= 1, \\ \lambda_1^{\mathrm{L}} &\leq 1 - \varepsilon_1\end{split}\]

よって \(\lambda_1^{\mathrm{L}},\lambda_1^{\mathrm{R}}\) の変化に対して，\(x\) は次のように変化する．

(7)#\[\begin{split}\lambda_1^{\mathrm{L}} &\colon 1 - \varepsilon_1 \to 0, \\ \lambda_1^{\mathrm{R}} &\colon \varepsilon_1 \to 1, \\ x &\colon X_0 + L_1\cdot\varepsilon_1 \to X_1\end{split}\]

つまりこの場合は \(f\) の定義域が \(L_1\cdot\varepsilon_1 \leq x \leq X_1\) に対応している． 特に small ε であることを考慮すると，\(0<x\leq X_1\) を扱っていることになる．

\((\delta_0,\delta_1,\delta_2)=(0,0,1,0)\) の場合
(8)#\[\begin{split}f(x) &= C_2, \\ x &= X_1\cdot\lambda_2^{\mathrm{L}} + X_2\cdot\lambda_2^{\mathrm{R}}, \\ \lambda_2^{\mathrm{L}} + \lambda_2^{\mathrm{R}} &= 1, \\ \lambda_2^{\mathrm{L}} &\leq 1 - \varepsilon_2\end{split}\]

よって \(\lambda_2^{\mathrm{L}},\lambda_2^{\mathrm{R}}\) の変化に対して，\(x\) は次のように変化する．

(9)#\[\begin{split}\lambda_2^{\mathrm{L}} &\colon 1 - \varepsilon_2 \to 0, \\ \lambda_2^{\mathrm{R}} &\colon \varepsilon_2 \to 1, \\ x &\colon X_1 + L_2\cdot\varepsilon_2 \to X_2\end{split}\]

つまりこの場合は \(f\) の定義域が \(X_1+L_2\cdot\varepsilon_2 \leq x \leq X_2\) に対応している． 特に small ε であることを考慮すると，\(X_1<x\leq X_2\) を扱っていることになる．

\((\delta_0,\delta_1,\delta_2)=(0,0,0,1)\) の場合
(10)#\[\begin{split}f(x) &= C_3, \\ x &= X_2\cdot\lambda_3^{\mathrm{L}} + X_3\cdot\lambda_3^{\mathrm{R}}, \\ \lambda_3^{\mathrm{L}} + \lambda_3^{\mathrm{R}} &= 1, \\ \lambda_3^{\mathrm{L}} &\leq 1 - \varepsilon_3\end{split}\]

よって \(\lambda_3^{\mathrm{L}},\lambda_3^{\mathrm{R}}\) の変化に対して，\(x\) は次のように変化する．

(11)#\[\begin{split}\lambda_3^{\mathrm{L}} &\colon 1 - \varepsilon_3 \to 0, \\ \lambda_3^{\mathrm{R}} &\colon \varepsilon_3 \to 1, \\ x &\colon X_2 + L_3\cdot\varepsilon_3 \to X_3\end{split}\]

つまりこの場合は \(f\) の定義域が \(X_2+L_3\cdot\varepsilon_3 \leq x \leq X_3\) に対応している． 特に small ε であることを考慮すると，\(X_2<x\leq X_3\) を扱っていることになる．

以上にして，多階段関数 \(f\) の定式化ができていることが確認できた．

4.2.2. 定式化の改良#

上記に与えた定式化は small ε を用いている点で不満が残る． これは「\(f\) が目的関数最小化の対象である」ことを仮定すれば，次のようにして解消できる．

(12)#\[\begin{split}& \mathrm{Minimize\colon}~ y \\ & \mathrm{subject~to\colon}~ \\ & y \geq f(x), \\ & f(x) := C_0\cdot \delta_0 + \sum_{i=1}^n C_i\cdot \delta_i, \\ & x = X_0\cdot \lambda_0 + \sum_{i=1}^nX_i\cdot\lambda_i^{\mathrm{R}} + \sum_{i=1}^nX_{i-1}\cdot\lambda_i^{\mathrm{L}}, \\ & x\geq B, \\ & \delta_0 + \sum_{i=1}^n \delta_i = 1, \\ & \lambda_0 = \delta_0, \\ & \lambda_i^{\mathrm{L}} + \lambda_i^{\mathrm{R}} = \delta_i, \, \forall i \in \{1,\ldots,n\}\end{split}\]

ここで多階段関数 \(f\) の踏面の数を一般化しておいた．

新たに追加した仮定がどのように機能するかを以下に見よう．

まず最小化問題を考える中で変数 \(x\) 自体も \(f\) の定義域ではなく，何らかの下界 \(B\) が与えられているとする 1上界については \(f\) が単調増加であることから陽に仮定しなかった．． 下界 \(B\) は多階段関数 \(f\) を目的関数とする何らかの定式化の中で， \(f\) 自体の定式化とは別の問題特有の制約条件の集まりから決まる値ともここでは考えられる値である．

さて多階段関数 \(f\) の形から，不連続点は原点か \(x=X_1\) の周りについて調べれば十分である．

最初に \(x=(X_0=)0\) については \(B=0\) であることを仮定して調べると次のとおり．

新たな変数 \(y\) の最小化を考えるとき，\(x\geq0\) で \(y\) の最小値は \(x=0\) のときであるから，\(\delta_0=1\) で他の \(\delta_i\) はすべて \(0\) である． よって原点で整合している．

次に \(0<B<X_1\) の場合を仮定して調べると， \(x\) の等式制約 (または定義式) について \(B\leq x< X_1\) から \(x=X_0\cdot\lambda_1^{\mathrm{L}} + X_1\cdot\lambda_1^{\mathrm{R}}\) となって，\(\delta_1\) のみが \(1\) で，他の \(\delta_0,\delta_i\) は \(0\) となる． つまり \(y\) の最小値は \(C_1\) となって整合している．

最後に \(B=X_1\) を仮定して \(x\geq X_1\) の場合を調べると， \(\delta_0=0\) で他の \(\delta_i\) の何れか一つが \(1\) になりえる． 一方でこの \(\{\delta_i\}_{i=1}^n\) の自由度の中で \(y\) の最小化を考えているので， \(\delta_1=1\) が選ばれることになり，最小値は \(C_1\) となる． このとき \(\lambda_1^{\mathrm{R}}=1\) であり，他の \(\lambda\) は \(0\) であって，\(x=X_1\) となる．つまり整合している．

以上から small ε を用いることなく，多階段関数 \(f\) を目的関数の下限とする最小化が記述できていることが確認できた．

注釈

さてもし \(x=X_1\) での \(f\) の値が \(C_1\) ではなく，床関数のように上に跳躍して \(C_2\) であったらどうなるだろうか． このときも \(B=X_1\) の場合に，\(\delta_0=0\) で他の \(\delta_i\) の何れか一つが \(1\) になりえる． \(y\) の最小化という意味では再び \(\delta_1=1\) が選ばれることになり，最小値は \(C_1\) となる． このことは \(f\) の定義と整合しない．

つまり最小化を考える場合には，不連続点では上に跳躍しないことが必要となる． このことを言い換えると，\(f\) が 下半連続 であることに対応している．

例えば天井関数 \(\lceil x\rceil\) は下半連続であるが，床関数 \(\lfloor x\rfloor\) はそうではない (上半連続である)．

4.2.3. 実装例#

多階段関数 \(f\) として次を考えよう．

(13)#\[\begin{split}f(x) = \begin{cases} 0 & (x=0), \\ 20 & (0 < x \leq 10), \\ 40 & (10 < x \leq 20), \\ 60 & (20 < x \leq 30) \end{cases}\end{split}\]

このとき PySIMPLE による実装例は次のとおりである． ここで \(x\) については定義式として扱い，変数と制約式の数を定式化の段階で事前に削減させている．

PySIMPLE Sample Code
 1def optimize(B, **kwds):
 2    from pysimple import Problem, Parameter, Variable, BinaryVariable, Element, Sum
 3
 4    i = Element(value=[1,2,3])
 5    X = Parameter(index=i)
 6    X[i] = 10*i
 7    C = Parameter(index=i)
 8    C[i] = 20*i
 9    B = Parameter(value=B)
10    
11    delta0 = BinaryVariable()
12    delta = BinaryVariable(index=i)
13    lmd_L = Variable(index=i, lb=0)
14    lmd_R = Variable(index=i, lb=0)
15    y = Variable()
16    x = Sum(X[i]*lmd_R[i], i) + X[1]*lmd_L[2] + X[2]*lmd_L[3]
17    x.name = 'x'
18    f = Sum(C[i]*delta[i], i)
19    
20    p = Problem(type=min)
21    p += y
22    p += y >= f
23    p += x >= B
24    p += delta0 + Sum(delta[i], i) == 1
25    p += lmd_L[i] + lmd_R[i] == delta[i]
26    p.solve(**kwds)
27    show(p, B, x, y)
28
29def show(p, B, x, y):
30    print('\n[Print]')
31    print(p.status)
32    print(B)
33    print(x.val)
34    print(y.val)
35
36# ---
37
38optimize(0-0.1, silent=True)
39optimize(0, silent=True)
40optimize(0+0.1, silent=True)
41optimize(10-0.1, silent=True)
42optimize(10, silent=True)
43optimize(10+0.1, silent=True)
44optimize(20-0.1, silent=True)
45optimize(20, silent=True)
46optimize(20+0.1, silent=True)
47optimize(30-0.1, silent=True)
48optimize(30, silent=True)
49optimize(30+0.1, silent=True)

上記を実行すると次の結果を得る．

Result
 1[Print]
 2NuoptStatus.OPTIMAL
 3B=-0.1
 4x.val=0
 5y.val=0.0
 6
 7[Print]
 8NuoptStatus.OPTIMAL
 9B=0
10x.val=0
11y.val=0.0
12
13[Print]
14NuoptStatus.OPTIMAL
15B=0.1
16x.val=9.999999999999998
17y.val=20.0
18
19[Print]
20NuoptStatus.OPTIMAL
21B=9.9
22x.val=9.999999999999998
23y.val=20.0
24
25[Print]
26NuoptStatus.OPTIMAL
27B=10
28x.val=9.999999999999998
29y.val=20.0
30
31[Print]
32NuoptStatus.OPTIMAL
33B=10.1
34x.val=20
35y.val=40.0
36
37[Print]
38NuoptStatus.OPTIMAL
39B=19.9
40x.val=20
41y.val=40.0
42
43[Print]
44NuoptStatus.OPTIMAL
45B=20
46x.val=20
47y.val=40.0
48
49[Print]
50NuoptStatus.OPTIMAL
51B=20.1
52x.val=30
53y.val=60.0
54
55[Print]
56NuoptStatus.OPTIMAL
57B=29.9
58x.val=30
59y.val=60.0
60
61[Print]
62NuoptStatus.OPTIMAL
63B=30
64x.val=29.999999999999996
65y.val=59.999999999999986
66
67[Print]
68NuoptStatus.INFEASIBLE
69B=30.1
70x.val=30.099999999999994
71y.val=0.0

不連続点およびその周りでの挙動が正しく反映されていることがわかる． また定義域を超えた下界が与えられた場合にも，正しく実行不可能となっている．

4.3. 下半連続関数#

下半連続関数の定義を次に与えよう．

下方位集合 (lowercontour set)

関数 \(f\colon A\to \mathbb{R}\) の \(c\) についての下方位集合 \(L_f(c)\) とは次に定める集合のことである．

(14)#\[L_f(c) := \{x\in A \mid f(x)\leq c \}\]

下半連続関数 (lower semicontinuous function)

関数 \(f\) が点 \(x\) で下半連続であるとは，\(f\) の下方位集合 \(L_f(c)\) が任意の \(c\in\mathbb{R}\) について閉集合であることをいう． そして関数 \(f\) が下半連続関数であるとは，\(f\) の定義域全体で下半連続であることをいう．

対になる概念として上半連続関数 (upper semicontinuous function) があるが，これは上方位集合 \(U_f(c)\) なるものを次で定義し， 下半連続関数の定義文について「下」を「上」に置換すればよい．

(15)#\[U_f(c) := \{x\in A \mid f(x)\geq c \}\]

4.3.1. 天井関数#

天井関数 \(f(x) = \lceil x\rceil\) は下半連続関数である．

例えば \(c=-1/2\) に対して，\(L_f(-1/2)=(-\infty,-1]\) であって，これは \(\mathbb{R}\) 上の閉集合である． また \(c=0\) に対して，\(L_f(0)=(-\infty,0]\) であって，これもまた \(\mathbb{R}\) 上の閉集合である． 他の任意の \(c\in\mathbb{R}\) については，これらと同じように考えることができて，次のように下方位集合を求めることができる．

(16)#\[L_f(c) = (-\infty,\lfloor c\rfloor]\]

これは \(\mathbb{R}\) 上の閉集合であるから，\(f\) は下半連続関数である．

多階段関数も上記の議論から，下半連続関数であることは明らかである．

4.3.2. 一点集合指示関数#

次に定める一点集合指示関数 \(\chi\colon \mathbb{R}\to\mathbb{B}\) は下半連続関数ではない．

(17)#\[\begin{split}\chi(x) := [x=1] = \begin{cases} 1 & (x=1), \\ 0 & (x\neq 1) \end{cases}\end{split}\]

実数 \(c\) について下方位集合は次のように求められる．

(18)#\[\begin{split}L_{\chi}(c) = \begin{cases} \emptyset & (c<0), \\ (-\infty,1)\cup(1,\infty) & (0<c<1), \\ \mathbb{R} & (c\geq 1) \end{cases}\end{split}\]

よって \(0<c<1\) について，下方位集合は \(\mathbb{R}\) 上の閉集合ではないから，\(f\) は下半連続関数でない．

\(\chi\) は下半連続関数ではないものの，上半連続関数である． 実際，上方位集合は次のように求められるからである．

(19)#\[\begin{split}U_{\chi}(c) = \begin{cases} \emptyset & (c>1), \\ \{1\} & (0<c<1), \\ \mathbb{R} & (c\leq 0) \end{cases}\end{split}\]

ところでこのことからもわかるように，次のように修正した関数は下半連続関数である．

(20)#\[\bar{\chi}(x) := -[x=1]\]

この場合，下方位集合は任意の \(c\in\mathbb{R}\) について閉集合になる．

(21)#\[\begin{split}L_{\chi}(c) = \begin{cases} \emptyset & (c<-1), \\ \{1\} & (-1<c<0), \\ \mathbb{R} & (c\geq 0) \end{cases}\end{split}\]

4.4. 不連続な区分線形関数#

多階段関数の線形な定式化はそのまま一般の不連続な区分線形関数 \(f\) へと定式化を拡張できる． それは次のとおりである．

(22)#\[\begin{split}& \mathrm{Minimize\colon}~ y \\ & \mathrm{subject~to\colon}~ \\ & y \geq f(x), \\ & f(x) := \sum_{i=1}^n \sum_{D=\mathrm{L},\mathrm{R}} C_i^D\cdot \lambda_i^D, \\ & x := \sum_{i=1}^n \sum_{D=\mathrm{L},\mathrm{R}} X_i^D\cdot\lambda_i^D, \\ & L\leq x\leq U, \\ & \sum_{i=1}^n \delta_i = 1, \\ & \lambda_i^{\mathrm{L}} + \lambda_i^{\mathrm{R}} = \delta_i, \, \forall i \in \{1,\ldots,n\}\end{split}\]

ここで \(f\) として下半連続性を仮定している．

\(\{\delta_i\}_{i=1}^n\) の要素の何れかが \(1\) であるとき， 第 \(i\) 番目の区分 (\(X_i^{\mathrm{L}}\leq x\leq X_i^{\mathrm{R}}\)) の線形関数が選ばれることになる．区分が境界値を含むかどうかは下半連続性が保証される範囲で自由とする． そしてその線形関数は左端と右端の値がそれぞれ \(C_i^{\mathrm{L}}\) と \(C_i^{\mathrm{R}}\) の値であり，凸結合になっている．

関連

参考文献

[1]

H. Paul Williams. Model Building in Mathematical Programming. Wiley, 5th editio edition, 2013. URL: https://www.wiley.com/en-us/Model+Building+in+Mathematical+Programming%2C+5th+Edition-p-9781118506172.

引用書式

BibTeX

目次