5. 内点法#
5.1. 導入#
内点法の基本的な事柄について以下にまとめる.
5.2. 小史#
単体法 は原理的に明快な側面をもち,且つその計算方法もそれほど難しい手続きを踏むものではない. このため単体法は 線形最適化問題 の実用的且つ効率的なアルゴリズムとして広く受け入れられてきた. 事実,経験的には問題の制約条件数の \(1.5\) 倍から \(3\) 倍程度の反復回数によって計算を終えることができ, 問題の規模の増大に対する単体法の計算量の増加は比較的穏やかである.
しかしながら線形最適化問題は多項式時間アルゴリズムではない. 実務に当たっては単体法の急所を狙ったような問題に遭遇することは, そうそうあることではなく計算量が爆発的に増大することはないかもしれないが, 万全を期するという点で単体法は弱いのである.
そのような背景で Leonid Genrikhovich Khachiyan による 1979 年の初めての多項式時間アルゴリズムである楕円体法を基礎として, 1984 年に Narendra Karmarkar は新しい多項式時間アルゴリズム 内点法 を提案した. 内点法は大規模な問題を単体法よりも速く解くことが可能であることを示したのである.
今日では内点法は計算効率について単体法を凌ぐ方法との評価 1小規模であれば単体法が圧倒的に速い.また大規模であっても常に内点法が優位とは限らない.問題というものは時に複雑で数値実験というステップは重要であり続ける (だろう). が定着し, 実用的なソフトウェアが開発されている. そのためオリジナルの Karmarkar の方法とそれに触発されて生まれた多くの方法 2本稿で紹介する主双対内点法は,東京工業大学の小島政和,水野眞治,吉瀬章子の三名,および同時期に統計数理研究所の田辺國士が開発したアルゴリズムである. を総称して内点法と人々は現在よんでいる.
5.3. 内点法の分類#
単体法は実行可能領域の境界を探索していく方法であったが, 内点法は実行可能領域の内部を逐次探索して最適解に到達する方法である. この内部で生成される点列 (逐次探索の方法,最適解への近付き方) をどのように構築していくかで,内点法の分類が行われる. 代表例を挙げよう.
-
3affine スケーリング法とも.affine 変換法は内点法に分類されるが,多項式時間アルゴリズムではない.Karmarkar の 1984 年の発表に先立つこと 1967 年に数学者の I.I.Dikin (ソ連) によって提案されていた.
affine 変換法 [1] 3affine スケーリング法とも.affine 変換法は内点法に分類されるが,多項式時間アルゴリズムではない.Karmarkar の 1984 年の発表に先立つこと 1967 年に数学者の I.I.Dikin (ソ連) によって提案されていた.
ポテンシャル減少法
パス追跡法
予測子・修正子法
対数障壁法
これらの方法は主問題,双対問題または両方を取り扱うかで記述のタイプが分かれ, それぞれ主内点法,双対内点法,主双対内点法とよぶ.
主双対最適性条件は内点法の一つであるパス追跡法を主双対内点法の枠組みで説明することができるので, これを基にして内点法についての説明を以下に行う.
5.4. パス追跡法(主双対内点法)#
パス追跡法は中心パスという経路を追跡して終端に行き着いたとき,その終端が最適解を与える方法である. ここに中心パスは次の連立式の解曲線 \((\vec{x}(\mu),\vec{\omega}(\mu),\vec{s}(\mu))\) として定義される. 但し,\(X=\operatorname{Diag}(\vec{x})\) および \(S=\operatorname{Diag}(\vec{s})\) である.
解曲線は \(\mu\) で目盛付される曲線であり,主双対最適性条件 (53) の対応からわかるように,\(\mu\rightarrow 0\) という極限で解曲線の終端としての最適解に到達する. ここで解曲線の各点をパラメータ \(\mu\) に対する 中心 という.
(1) では \(\vec{x},\vec{s}\) の非負条件がより厳しい正値条件となっている (それ故,第一式の意味するところである \(s_ix_i=0\) では要求できず正値となる).
つまり境界が除かれており,この意味で内部の位置を指示していることから内点法の一種とされている. もっと言えば,パス追跡法は \(\mu\rightarrow 0\) に向かって単調に減少し収束する実数列
の各 \(\mu^{(k)}\) に対する中心 \((\vec{x}(\mu^{(k)}),\vec{\omega}(\mu^{(k)}),\vec{s}(\mu^{(k)}))\) を逐次近似的に求めて最適解に迫ろうという方法である. 但し近似解を求める際には正値条件が満たされているか注意する.
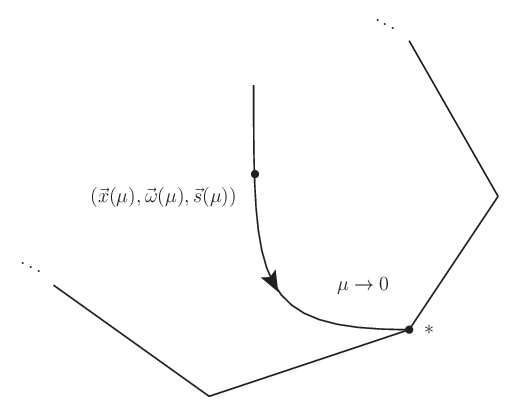
図 5.1 内点法のイメージ#
各反復での \(\mu^{(k)}\) としては,Euclid ノルム \(\|XS\vec{1} - \mu\vec{1}\|_2\) が最小となるよう次の値に設定することができる.
\((\vec{x}^{(k)})^{\top}\vec{s}^{(k)}\) の値よりも,\(\mu\) が小さければ,より \(\{\mu^{(k)}\}_k\) が単調減少すると考えられるので,更に(例えば)次の何れかに改良するとよいことが知られている.
近似解に頼ろうとするのは \(XS\vec{1} = \mu\vec{1}\) が非線形方程式だからに他ならない. 近似の方法は線形近似によって行う. ここに線形近似した \(1\) 次方程式を逐次解くことにより,解に収束する点列を生成する反復法を Newton 法という. 具体的には次の手順を踏む.
\(k\) 回目の反復によって \(k\) 番目の中心 \((\vec{x}(\mu^{(k)}),\vec{\omega}(\mu^{(k)}),\vec{s}(\mu^{(k)}))\) が得られているとする.
\(k+1\) 番目の中心 \((\vec{x}(\mu^{(k+1)}),\vec{\omega}(\mu^{(k+1)}),\vec{s}(\mu^{(k+1)}))\) は,次で線形近似する.
(5)#\[\begin{split}\begin{bmatrix} \vec{x}(\mu^{(k+1)}) \\ \vec{\omega}(\mu^{(k+1)}) \\ \vec{s}(\mu^{(k+1)}) \end{bmatrix} = \begin{bmatrix} \vec{x}(\mu^{(k)}) + \alpha\Delta\vec{x} \\ \vec{\omega}(\mu^{(k)}) + \alpha\Delta\vec{\omega} \\ \vec{s}(\mu^{(k)}) + \alpha\Delta\vec{s} \end{bmatrix} ~~ (\alpha > 0)\end{split}\]このとき近似の程度を担う因子 \(\alpha\) は \(k+1\) 番目での正値条件が満足されているように注意しなければならない. 具体的な技術的なコメントは後のステップで述べる.
線形近似を行うために中心パスに沿った変化分 \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) を求める.そのために (1) に対して,次を代入し変化分 \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) を求める.
(6)#\[\begin{split}\begin{bmatrix} \vec{x} \\ \vec{\omega} \\ \vec{s} \end{bmatrix} = \begin{bmatrix} \vec{x}(\mu^{(k)}) + \Delta\vec{x} \\ \vec{\omega}(\mu^{(k)}) + \Delta\vec{\omega} \\ \vec{s}(\mu^{(k)}) + \Delta\vec{s} \end{bmatrix}\end{split}\]解くべき式は解くべき変数について線形(二次の変化量は無視)なので, 線形近似の枠内で厳密に且つ容易に解くことができる.
(1) を変化分 \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) について解く.二次の変化量を無視すれば,代入によってまず次のように整理される.整理は左辺に方程式の変数,右辺に定数 \(\vec{r}_{\mathrm{P}},\vec{r}_{\mathrm{D}},\vec{r}_{\mathrm{C}}\) がくるようにした.但し,\(X^{(k)}=\operatorname{Diag}(\vec{x}(\mu^{(k)}))\) および \(S^{(k)}=\operatorname{Diag}(\vec{s}(\mu^{(k)}))\) である.
(7)#\[\begin{split}(1^{\circ})\colon&~ A\Delta\vec{x} = \vec{r}_{\mathrm{P}}, \\ (2^{\circ})\colon&~ A^T\Delta\vec{\omega} + \Delta\vec{s} = \vec{r}_{\mathrm{D}}, \\ (3^{\circ})\colon&~ S^{(k)}\Delta\vec{x} + X^{(k)}\Delta\vec{s} = \vec{r}_{\mathrm{C}}\end{split}\]ここで定数 \(\vec{r}_{\mathrm{P}},\vec{r}_{\mathrm{D}},\vec{r}_{\mathrm{C}}\) は次のとおりである.
(8)#\[\begin{split}\vec{r}_{\mathrm{P}} &= \vec{b} - A\vec{x}(\mu^{(k)}), \\ \vec{r}_{\mathrm{D}} &= \vec{c} - A^T\vec{\omega}(\mu^{(k)}) - \vec{s}(\mu^{(k)}), \\ \vec{r}_{\mathrm{C}} &= \mu^{(k)}\vec{1} - X^{(k)}S^{(k)}\vec{1}\end{split}\]連立方程式から,\((2^{\circ})\) を \(\Delta\vec{s}\) について解いて,\((3^{\circ})\) から \(\Delta\vec{s}\) を消去して,\(\Delta\vec{x}\) について解くと次が得られる.
(9)#\[\Delta\vec{x} = (S^{(k)})^{-1} (\vec{r}_{\mathrm{C}} - X^{(k)}\vec{r}_{\mathrm{D}} + X^{(k)} A^T \Delta\vec{\omega})\]これを \((1^{\circ})\) に代入することで,\(\Delta\vec{x}\) を消去して \(\Delta\vec{\omega}\) について整理できて,次が得られる.
(10)#\[(4^{\circ})\colon~ H^{(k)}\Delta\vec{\omega} = \{\vec{r}_{\mathrm{P}} - A(S^{(k)})^{-1}(\vec{r}_{\mathrm{C}} - X^{(k)}\vec{r}_{\mathrm{D}})\}\]ここで,次の正方行列を定義した.
(11)#\[H^{(k)} = A(S^{(k)})^{-1}X^{(k)}A^T\]よって,後は以下の手順に従って \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) を求めることで, \((1^{\circ})\) から \(A\) の逆を求めるというような数値的に困難な道を回避できる.
\((4^{\circ})\) から \(\Delta\vec{\omega}\) を求める.
求めた \(\Delta\vec{\omega}\) を \((2^{\circ})\) に代入して,\(\Delta\vec{s}\) を求める.
求めた \(\Delta\vec{s}\) を \((3^{\circ})\) に代入して,\(\Delta\vec{x}\) を求める.
注釈
解こうとした連立方程式 \((1^{\circ})\) から \((3^{\circ})\) をベクトル行列表記で整理すると次のとおりである.
(12)#\[\begin{split}\begin{bmatrix} A & 0 & 0 \\ 0 & A^{\top} & 1 \\ S^{(k)} & 0 & X^{(k)} \end{bmatrix} \begin{bmatrix} \Delta\vec{x} \\ \Delta\vec{\omega} \\ \Delta\vec{s} \end{bmatrix} = \begin{bmatrix} \vec{r}_{\mathrm{P}} \\ \vec{r}_{\mathrm{D}} \\ \vec{r}_{\mathrm{C}} \end{bmatrix}\end{split}\]ここから \(\Delta\vec{s}\) を消去するとき,次の連立方程式を考えていたことに相当している.
(13)#\[\begin{split}\begin{bmatrix} 0 & A \\ -X^{(k)}A^{\top} & S^{(k)} \end{bmatrix} \begin{bmatrix} \Delta\vec{\omega} \\ \Delta\vec{x} \end{bmatrix} = \begin{bmatrix} \vec{r}_{\mathrm{P}} \\ \vec{r}_{\mathrm{C}} - X^{(k)}\vec{r}_{\mathrm{D}} \end{bmatrix}\end{split}\]すると,左辺の係数行列を \(M\) とするとき,\(H^{(k)}\) とは Schur 補行列 に他ならないことがわかる.
(14)#\[M/S^{(k)} = 0 - A(S^{(k)})^{-1}(-X^{(k)}A^{\top}) = A(S^{(k)})^{-1}X^{(k)}A^{\top} = H^{(k)}\]\(X^{(k)}\) と \(S^{(k)}\) が対角行列で可換であり対称行列であることから,\(H^{(k)}\) は対称行列となっている.
(15)#\[(H^{(k)})^{\top} = H^{(k)}\]特に,\(\operatorname{rank}A=m\) でフルランクならば,\(H^{(k)}\) は正定値行列でもある.
求めた \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) は非線形項を無視して求めたため,そのまま次の反復点を,\((\vec{x}+\Delta\vec{x},\vec{\omega}+\Delta\vec{\omega},\vec{s}+\Delta\vec{s})\) とすると,解曲線である中心パスに乗らない.
しかし近いところにはあるはずなので,(5) にあるとおり,ステップサイズを \(\alpha\) として,\((\vec{x}+\alpha\Delta\vec{x},\vec{\omega}+\alpha\Delta\vec{\omega},\vec{s}+\alpha\Delta\vec{s})\) とする.経験的に \(\alpha\) は各変数の正値条件が満たされる範囲で設定する.
具体的には次の値を求める.
(16)#\[\begin{split}\alpha_P &:= \min_{\substack{i\in\{1,\cdots,n\}\\ \Delta\vec{x}<0}} \frac{x_i}{-\Delta x_i}, \\ \alpha_D &:= \min_{\substack{i\in\{1,\cdots,m\}\\ \Delta\vec{\omega}<0}} \frac{\omega_i}{-\Delta \omega_i}, \\ \alpha &:= \min(\gamma \alpha_P, \gamma \alpha_D, 1)\end{split}\]ここで,次の反復点が正値でなければならないので,差分が負であるものの中から選択している. そして,\(\alpha\) が \(1\) を超えてしまうと,より中心パスから離れることが強く期待されるので,\(\min(\bullet,1)\) とし, \(\gamma\) を \(0<\gamma \lesssim 1\) で,十分に \(1\) に近い定数とすることで \(\gamma\alpha_P\) および \(\gamma\alpha_D\) としている.なお,\(\gamma=0.9999\) のように実務にあたって設定を行う.
以上によって,逐次,中心パスに沿った変化分 \((\Delta\vec{x},\Delta\vec{\omega},\Delta\vec{s})\) を求め, 点列を辿っていくのがパス追跡法による内点法である.
5.5. 例題#
PySIMPLE のチュートリアルにもある 油田計画問題 は,本稿で述べた主双対内点法の説明に従って解くことができて,中心パスをいくつかの初期点について描くと 図 5.3 のようになる.
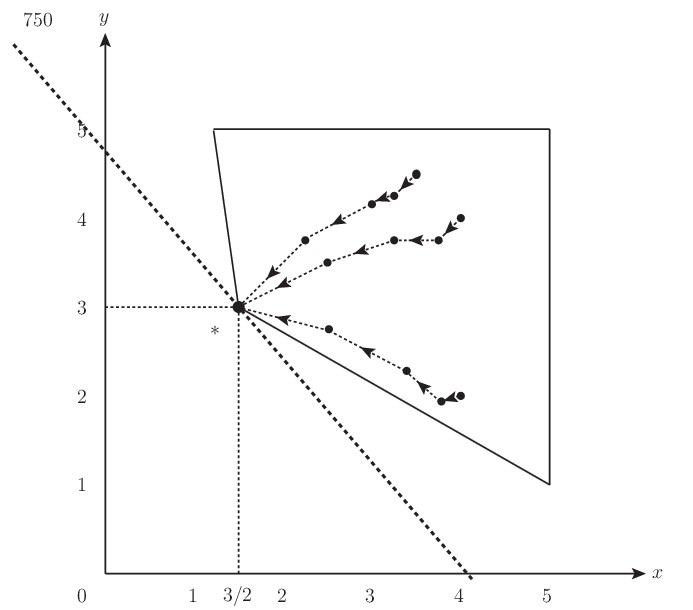
図 5.3 油田計画問題への内点法の適用#
最適解は単体法と違って,内点法では内点を与えるので収束判定条件を設ける必要がある. 収束判定条件を \(\vec{x}^{\top}\vec{s}<10^{-7}\) とするとき,何れも \(13\) 回程度の反復で収束判定される. 図では \(5\) 反復点ほどしか見えないが,実際には最適解の非常に近い点にたどり着いている. 本問題に関する限りでは,単体法の反復回数にはおよばないが,このような小規模問題ではなく, 大規模問題でも今の反復回数は単体法ほど増加しない.
関連
用語集
参考文献
I. I. Dikin. Iterative solution of problems of linear and quadratic programming. Dokl. Akad. Nauk SSSR, 174(4):747–748, 1967. URL: http://mi.mathnet.ru/dan33112.
水野眞治. 学習・研究用テキスト (最適化, 線形計画法, 内点法, 数理計画法). URL: https://www.nakatalab.iee.e.titech.ac.jp/text/mizuno.html.
中田和秀. 主双対内点法. オペレーションズ・リサーチ = Communications of the Operations Research Society of Japan : 経営の科学, 64(4):218–224, 2019. URL: https://orsj.org/wp-content/corsj/or64-4/or64_4_218.pdf.
小島政和, 土谷隆, 水野眞治, and 矢部博. 内点法 (経営科学のニューフロンティア 9). 朝倉書店, 2001. ISBN 978-4-254-27519-3. URL: https://www.asakura.co.jp/detail.php?book_code=27519.
原田耕平. 数理計画法の誕生と発展(その 4). 数理システム NUOPT メールマガジン, feb 2009. URL: https://www.msi.co.jp/solution/nuopt/mailmagazine/backnumber0902.html#6.
今野浩. カーマーカー特許とソフトウェア: 数学は特許になるか (中公新書 1278). 中央公論新社, 1995. ISBN 4-12-101278-X. URL: https://ndlsearch.ndl.go.jp/books/R100000002-I000002478134.
久保幹夫, 田村明久, and 松井知己. 応用数理計画ハンドブック. 朝倉書店, 2002. ISBN 978-4-254-27021-1. URL: https://www.asakura.co.jp/detail.php?book_code=27021.
福島雅夫. 新版 数理計画入門. 朝倉書店, 2011. ISBN 978-4-254-28004-3. URL: https://www.asakura.co.jp/detail.php?book_code=28004.
引用書式
