2. 線形最適化問題#
2.1. 導入#
線形最適化問題を理論的に述べるために必要な話題について以下にまとめる.
2.2. 定義#
線形最適化問題
目的関数および制約式が定数項を許した線形式であるとき,その数理最適化問題を線形最適化問題 (Linear Optimization) もしくは線形計画問題 (Linear Programming) という. 単に LO とか LP とも.
2.3. 小史#
線形最適化問題の歴史は,第二次世界大戦時に於ける米空軍の 1942 年の軍事作戦 (後の SCOOP 1Scientific Computation of Optimum Programs 計画 [1, 2]) の研究に遡ることができる.
第二次世界大戦中,輸送船の不足が連合国軍にとって危険な供給障害となった. オランダから米国に移住した経済学者の Tjalling Charles Koopmans はこの問題を最適計画問題として捉え, 彼は線形計画法によって艦船の航行の最適解を得るに到ったという.
また George Bernard Dantzig は SCOOP 計画にリーダーの一人として加入し, 戦後の 1947 年に米空軍の線形計画問題として定式化されたある計画問題を解くために 単体法 (simplex method) 2単体法という名前は,Danzig がそのアルゴリズムを試した簡単な一つの例題に由来している [3].その例題は制約条件が \(\sum_{j=1}^n x_j\leq 1\) および \(x_j\geq 0\) からなっており,これらの条件は \(n\) 次元空間の単体 (simplex) とよばれる三角形の高次元拡張図形の方程式となっている.現在では,この特殊な場合に限らず,線形な制約式で定まる一般の凸多胞体についても,単体法という用語が用いられている. を考案した. この出来事を境に,生産管理における非常に広範囲の見かけ上は全く無関係な問題が,線形計画問題 3当初,線形計画問題 を Dantzig は「Programming in a Linear Structure」(線形構造における計画) と呼んでいたが,Koopmans に示唆されて「Linear Programming」という名称になったという. に還元されて新分野の開拓にまで至った.
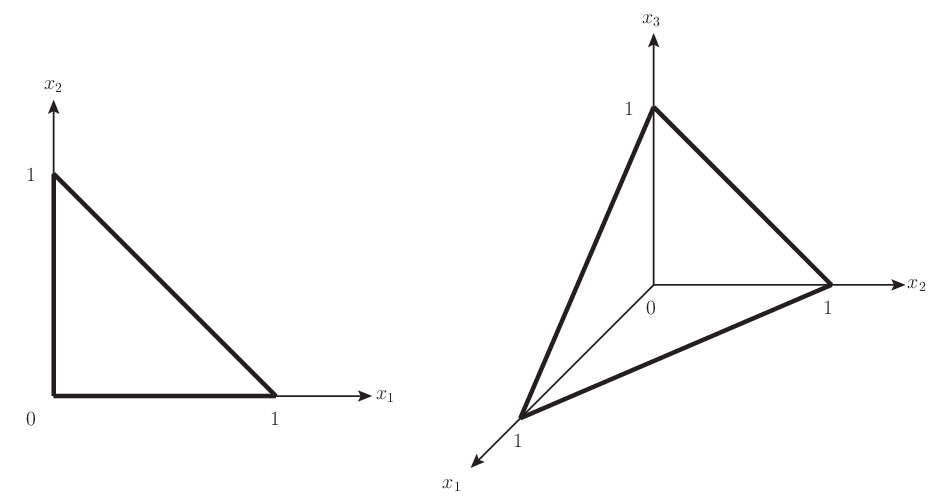
図 2.1 \(\sum_{j=1}^n x_j\leq 1\) および \(x_j\geq 0\) について,\(n=2\) および \(n=3\) に対応する二次元単体(三角形)と三次元単体(四面体)#
歴史を語る上では旧ソ連の様々な科学者らもまた多くの貢献をなしているが, 政治的に厳しい統制下にあったことや米国や西側諸国などとの交流が自由ではなかったこともあって, それら貢献が雪解けのように後年知られるようになることも珍しくはない. このことは数理最適化の分野に限ったことではない.
2.4. 基本性質#
線形最適化問題については次のことが基本的である.
-
4非負制約以外の制約式が等式制約となっているため,等式標準形と強調することがある.
線形最適化問題は標準形 4非負制約以外の制約式が等式制約となっているため,等式標準形と強調することがある. と呼ばれる次の式の形にいつでも整理できる.
(1)#\[\begin{split}& \mathrm{Minimize\colon}~ f(\vec{x}) = \vec{c}^{\top}\vec{x} \\ & \mathrm{Subject~to\colon}~ \\ & A\vec{x} = \vec{b}, \\ &\vec{x} \geq \vec{0}\end{split}\]実行可能領域は凸多胞体 (convex polytope) の形状をしている.
最適解は実行可能領域である凸多胞体の何れかの端点である.
上記の事柄を順に説明すると次のとおり.
2.4.1. 標準形について#
目的関数は線形であるから,その一般形はある定数ベクトル \(\vec{c}\) との線形結合となっている. そして制約条件について,等式制約と非負制約のみからなることは次のとおりである.
すべての自由変数は 非負変数へ分解 できた. またスラック変数を用いることで,不等式制約を等式制約に直すことができる. ここでスラック変数はすべて非負にとっている. よって元の変数の集まりにスラック変数の集まりを追加しても, それらはすべて非負変数である.
以上から,制約条件は等式制約と非負制約にまとめることができる.
2.4.2. 実行可能領域の形状について#
高次元の多面体のことを多胞体 (polytope) という. 多胞体は超平面で囲われた図形であり, 特に凸集合であるような多胞体を凸多胞体という.
今,線形最適化問題の実行可能領域の形状を問うとき,この図形を表す集合は凸集合となっている. それは次のとおり.
線形最適化問題であるから,一般性を失わず標準形を仮定できる. よって変数の数を \(n\) 個とすれば,実行可能領域 \(C\) は次の集合である.
任意の \(\vec{x},\vec{y}\in C\) および任意の \(\alpha\in[0,1]\) に対して, 次を定める.
このとき \(\vec{z}\) の各成分は非負成分の非負倍の線形結合であるから,それ自身の成分もまた非負である. つまり \(\vec{z}\in\mathbb{R}_{\geq0}\) である.
また \(A\vec{z} = \alpha A\vec{x} + (1-\alpha) A\vec{y} = \alpha\vec{b} + (1-\alpha)\vec{b} = \vec{b}\) が従う. よって以上から \(\vec{z} \in C\) である.
ところで \(\vec{z}\) は凸結合であるから,これは集合 \(C\) が凸集合であることを意味する.
2.4.3. 最適解の位置について#
目的関数が線形であることから,超平面を可能な限り平行移動していった位置に最適解があると考えられる. そこで実行可能領域である凸多胞体の端点として \(\{P_i\}_{i\in I}\) をとるとき, 任意の実行可能解 \(\vec{x}\) を次の凸結合で表す [4].
ここで各 \(i\) について,\(\alpha_i\geq0\) かつ \(\sum_{i\in I}\alpha_i = 1\) である. 今,最適化として最小化を考え,目的関数を \(f\) とおく. そして各端点に限定した中で最も小さい値を \(m^*\) とする.
このとき \(f\) が線形であることから,任意の実行可能解 \(\vec{x}\) について次が成り立つ.
つまり \(m^*\) は端点に限らず,実行可能領域全体で最小値を与える.
端点以外の場合として凸領域の境界があり得るが,これは端点を含んでいるので,この意味でも主張は満足されている 5このような場合には境界すべての各点が最適解を与える訳だから,何か他の新しい要求についての制約条件を課して,尖らせることで最適解を一意にすることができる.つまりもう少し厳しいことを要求できる余地があることをこの状況は述べている..
ところで複数の端点 \(\{P_j\}_{j\in J\subsetneq I}\) で最小値 \(m^*=f(P_j)\) を与える可能性がある. この場合にはこれらの点のいかなる凸結合 \(\vec{x}_J\) に対しても,やはり同じ最小値 \(m^*\) を与える. これは次のとおりである.
前提から \(\bar{j}\in \bar{J}=I\setminus J\) に対しては最小値を与えないから,\(f(P_{\bar{j}}) > m^*\) が従う. ここで次の凸結合をとる (各 \(j\) について,\(\beta_j\geq0\) かつ \(\sum_{j\in J}\beta_j = 1\) とする).
すると \(f\) の線形性と \(\vec{x}_J\) が凸結合であることから,直ちに次の評価が得られる.
さて一方で,\(\vec{x}_J\) と書けない他の任意の実行可能解 \(\vec{x}_{\bar{J}}\) は, すべての端点についての凸結合をとる必要がある.
すると \(\vec{x}_{\bar{J}}\) での目的関数値として次の評価ができる.
故に \(f(\vec{x})=m^*\) となるのは,最小値を与える端点の凸結合 \(\vec{x}_J\) に限られる.
以上に述べた線形最適化問題の基本的な性質は単体法とよばれる解法の論拠となる.
2.5. ベクトル行列記法#
線形最適化問題の定式化について理論的側面で整理する際には, 線形代数との親和性からベクトルと行列で記述することが専らである. 先に述べた標準形 (1) はその最たる一例である.
ここでは下記に再掲する標準形について,それらは単体法を理解するうえで,基本的な概念や名称について述べる.
2.5.1. 基底変数と非基底変数#
変数について
等式制約へと変形させるために,一般に \(\vec{x}\) はスラック変数も含む.このためその分だけ行列 \(A\) は正方行列のサイズからずれる.
不等号は,ベクトルの各成分ごとに,記された不等号が両辺で成立することを意味する.
基底変数,非基底変数
等式標準形で線形最適化問題を書いたとき,全部で \(m\) 個の等式制約と \(n\) 個の変数があったとする.但し,\(m\leq n\) とする.
非基底変数とは,\(m\) 個ある等式制約が解けるよう,全部で \(n\) 個ある変数のうち,\(n-m\) 個の余剰な変数を \(0\) と置いた変数のことをいう.
基底変数とは,非基底変数でない変数のことを言う.
基底変数のうち,\(0\) の値をとってしまっている変数のことを特に退化した基底変数という.
基底変数ベクトル,非基底変数ベクトル
基底変数を成分にもつベクトルを基底変数ベクトル \(\vec{x}_B\) という.
非基底変数を成分にもつベクトルを非基底変数ベクトル \(\vec{x}_N\) という.
行列 \(A\) について
基底変数と非基底変数の総数を \(n\) とし,基底変数の総数を \(m\) とする.つまり行列 \(A\) としては \(m\times n\) の型を考える.
\(\operatorname{rank} A=m\) とし,基底変数はすべて独立変数で退化がないものとする.
基底行列,非基底行列
基底変数ベクトルおよび非基底変数ベクトルに作用する \(A\) の小行列をそれぞれ \(B,N\) とかくとき,\(B\) を基底行列,\(N\) を非基底行列という.
\(B\) としてはしばしば正則に限る.
\(A\) の転置に気を付ける.
(12)#\[\begin{split}A = \begin{bmatrix} B & N \end{bmatrix} \Leftrightarrow A^{\top} = \begin{bmatrix} B^{\top} \\ N^{\top} \end{bmatrix}\end{split}\]
2.5.2. 線形最適化問題の構造#
標準形を \(\vec{x}_B,\vec{N},B,N\) で書き直して, 線形最適化問題の構造をこれら二つの要因について言及できる.
基底解
非基底変数ベクトル \(\vec{x}_N\) を \(\vec{0}\) と置いた次は基底解とよばれる.
(13)#\[(\vec{x}_B , \vec{x}_N = \vec{0})\]実行可能基底解
制約条件 \(A\vec{x} = \vec{b}\) は次のように書き直せる.
(14)#\[B\vec{x}_B + N\vec{x}_N = \vec{b}\]\(B\) が正則だとすると,\(\vec{x}_N=\vec{0}\) と置いて次の基底解が得られる.
(15)#\[(\vec{x}_B , \vec{x}_N) = (B^{-1}\vec{b} , \vec{0})\]特に \(B^{-1}\vec{b}\geq\vec{0}\) が成立しているならば,\(\vec{x}_B\geq 0\) であるから,実行可能解としての端点解となって,これを実行可能基底解とよぶ.
ピボット操作
実行可能基底解に対して,基底変数と非基底変数を入れ替えた基底解が,再び実行可能基底解となるとき,この操作をピボット操作 (枢軸演算とも) という.
2.5.3. 最適性条件#
基底解の何れかは最適解の可能性がある. 適切にピボット操作を繰り返すことで,最適解に至ることになる. このために,最適解かどうかを判定する必要がある. それは次のとおり.
単体乗数
次の \(\vec{\pi}\) を単体乗数 (simplex multiplier) という.
(16)#\[\vec{\pi} = (B^T)^{-1}\vec{c}_B\]但し目的関数を基底変数と非基底変数とで書き直した時の係数を次のように置いた.
(17)#\[f(\vec{x}) = \vec{c}^{\top}\vec{x} = \vec{c}_B^{\top}\vec{x}_B + \vec{c}_N^{\top}\vec{x}_N\]単体辞書,相対費用係数
制約条件 \(A\vec{x}=\vec{b}\) を基底変数ベクトル \(\vec{x}_B\) を非基底変数ベクトル \(\vec{x}_N\) で書き直すと,\(B\vec{x}_B + N\vec{x}_N = \vec{b}\) であった.これから \(B\) が正則ならば,基底変数は非基底変数によって次ののように表される.
(18)#\[\vec{x}_B = B^{-1}\vec{b} - B^{-1}N\vec{x}_N\]これを用いて,元の標準形を非基底変数のみで書き直せば次のとおりである.
(19)#\[\begin{split}& \mathrm{Minimize\colon}~ f(\vec{x}_N) = \vec{\gamma}^{\top}\vec{x}_N + \vec{\pi}^{\top}\vec{b} \\ & \mathrm{Subject~to\colon}~ \\ &B^{-1}\vec{b} - B^{-1}N\vec{x}_N \geq \vec{0}, \\ &\vec{x}_N \geq \vec{0}\end{split}\]上記のうち,非負制約を除いた等式系を単体辞書 (simplex dictionary) または単に辞書という.
6経済学の文脈で機会費用 (opportunity cost) の概念を線形最適化問題で説明するために,この名称を用いることもある.なおここで次を定義した.これを非基底変数ベクトル \(\vec{x}_N\) の相対費用係数 (または単に相対費用 (relative cost)) という.相対費用は他にも被約費用 (reduced cost) や限界費用 (marginal cost) などの様々な異称がある 6経済学の文脈で機会費用 (opportunity cost) の概念を線形最適化問題で説明するために,この名称を用いることもある..
(20)#\[\vec{\gamma} = \vec{c}_N - N^{\top}\vec{\pi}\]目的関数は \(\vec{\gamma}^{\top}\vec{x}_N\) という変数部分と定数項 \(\vec{\pi}^{\top}\vec{b}\) に分かれることになる.
最適性条件
実行可能解に対して,相対費用係数が次を満たす場合を考える.
(21)#\[\vec{\gamma} \geq \vec{0}\]すると実行可能解ならば,\(\vec{x}_N \geq \vec{0}\) を満たすので,上記の相対費用係数の条件と合わせて,目的関数は \(\vec{x}_N=\vec{0}\) (端点解) のとき最小値として次の値をとる.
(22)#\[f^*(\vec{x}_N=\vec{0}) = \vec{\pi}^{\top}\vec{b}\]このとき基底解は最適解となり,そうでない場合には単に実行可能基底解となる.即ち,相対費用係数の条件 (21) は最適性の条件を与えている.このことから (21) を線形最適化問題の最適性条件という.
\(\vec{\gamma}\) の第一項は非基底変数からの正の寄与,第二項は基底変数も含めた負にもなりえる寄与となっている.これら二つの項の相対的な大小が目的関数値(費用に相当)の改善・悪化を示すことから,相対費用とよんでいる.
7被約は reduced の訳語であるが,数学色の強い単語であり,日常的な日本語ではほとんど使われない.被約は「約される」という意味合いが込められており,簡約・縮減・削減されるものを形容する.ここでは最小化したい目的関数値の改善を意識しているともいえる.一方で限界費用の限界は,どこまでの悪化を意識しているかともいえる.\(\vec{\gamma}\) のある第 \(k\) 成分が \(\gamma_k<0\) を満たすとき,基底外の変数(非基底変数)を増やすほど,目的関数が改善するため,これは費用を縮減できることに相当している.このことから,ピボット操作では目的関数を改善する非基底変数を選び出すため,相対費用とよぶよりも,被約費用とよぶ方が幾らか自然なときがある 7被約は reduced の訳語であるが,数学色の強い単語であり,日常的な日本語ではほとんど使われない.被約は「約される」という意味合いが込められており,簡約・縮減・削減されるものを形容する.ここでは最小化したい目的関数値の改善を意識しているともいえる.一方で限界費用の限界は,どこまでの悪化を意識しているかともいえる..
最適基底解,最適基底行列
最適性条件を満たす実行可能基底解を最適基底解という.そしてこのときの基底行列を最適基底行列 (単に最適基底とも) という.
以上のように線形最適化問題は,ベクトル行列記法によって整理される.
関連
用語集
参考文献
Saul Gass. THE LIFE AND TIMES OF THE FATHER OF LINEAR PROGRAMMING. 2005. doi:https://doi.org/10.1287/orms.2005.04.15.
Air Force Salutes Project SCOOP. 2007. doi:https://doi.org/10.1287/orms.2007.06.15.
M. I. Romakin. 数学新書 33 経済のための線型計画法入門. 東京図書, 1963. doi:https://doi.org/10.11501/1371247.
後藤儀一郎. 線形計画法 -最適値の導出について-. 駒大経営研究, 3(4):105, 1972. URL: https://komazawa-u.repo.nii.ac.jp/records/2011280.
近藤次郎. オペレーションズ・リサーチ (ORライブラリー1). 日科技連出版社, 1973. URL: https://dl.ndl.go.jp/pid/11982839.
ブラッケット. 戦争研究. みすず書房, 1964. URL: https://dl.ndl.go.jp/pid/9544596.
矢部博. 工学基礎 最適化とその応用. 数理工学社, 第2版 edition, 2024. ISBN 978-4-86481-111-8. URL: https://www.saiensu.co.jp/search/?isbn=978-4-86481-111-8&y=2024.
家富淳 and 岩永二郎. 数理計画法の誕生と発展(その 2). 数理システム NUOPT メールマガジン, aug 2008. URL: https://www.msi.co.jp/solution/nuopt/mailmagazine/backnumber0808.html#5.
久保幹夫, 田村明久, and 松井知己. 応用数理計画ハンドブック. 朝倉書店, 2002. ISBN 978-4-254-27021-1. URL: https://www.asakura.co.jp/detail.php?book_code=27021.
福島雅夫. 新版 数理計画入門. 朝倉書店, 2011. ISBN 978-4-254-28004-3. URL: https://www.asakura.co.jp/detail.php?book_code=28004.
引用書式
