3. 単体法#
3.1. 導入#
単体法 (Simplex method)
単体法とは,ある一つの端点解 (実行可能基底解) \(P_1\) から始めて, 目的関数値が改善するよう,ピボット操作によって隣接する端点解 \(P_2,P_3,\ldots\) に次々と移動して, 最終的に最適性条件を満足する最適解に到達しようとする手法である.
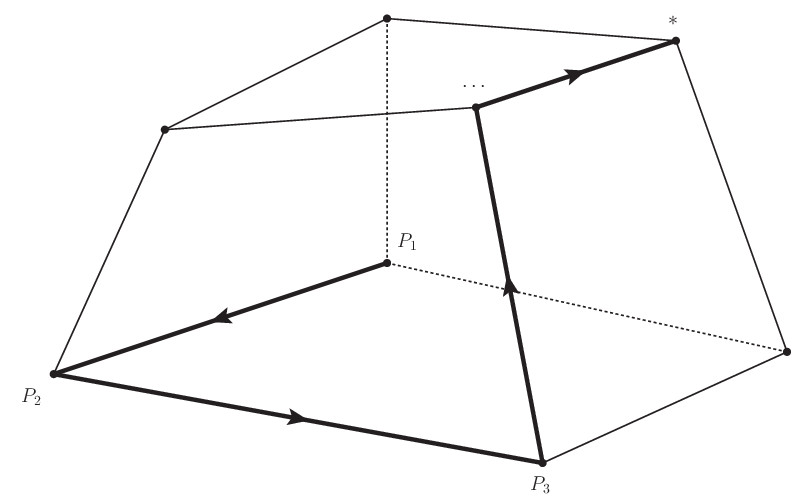
図 3.6 単体法の概念図#
注釈
単体法は最適解の候補である端点の座標を手当たり次第に求めず, 手順を追って次第に最適解に近付いていく方法である.
手当たり次第に求めようとすると,未知数が \(k\) 個あり,非負条件を含めた制約条件としての \(1\) 次不等式が \(n\) 個あれば,\(k\) 次元超平面の交点数は高々 \({}_nC_k\) 個ある.\(n,k\) が小さいときは手当り次第に端点解を求めても良いかもしれないが, 問題の規模が大きくなるとそうもいかないことがわかる.
3.2. 準備#
線形最適化問題は次の標準形にいつでも直せた.
ここで基底変数と非基底変数の自由度は次だとする.
制約式 \(A\vec{x} = \vec{b}\) の総数 (基底変数 \(\{[\vec{x}_B]_i\}_{i\in I}\) の総数) を \(m=|I|\) とし,全変数 \(\{[\vec{x}]_{i^{\prime\prime}}\}_{i^{\prime\prime}\in I^{\prime\prime}}\) の総数 (基底変数と非基底変数の総数)を \(n=|I^{\prime\prime}|\) とする.そして,非基底変数 \(\vec{x}_N\) の各成分を \(i^{\prime}\in I^{\prime}\) で添字付けることにする.
係数行列 \(A\) は \(\operatorname{rank} A=m\) とし,次のように基底行列 \(B\) と非基底行列 \(N\) に分解しておく.
そして上記の標準形は非基底変数のみで次のように書き直すことができた.
併せて以下の量を定義した.
これらはそれぞれ単体乗数,相対費用係数とよんだ.
このように問題を整理するとき,次の最適性条件が満たされるならば,実行可能解は最適解となった.
3.3. 単体法の手続き#
単体法とは実行可能基底解が最適解ではないとき, 次の端点解に至るためのピボット操作を以下の要領で決定する手続きである.
最適解でないということは,\(\vec{\gamma} \geq \vec{0}\) を満たさない成分が少なくとも一つあることを意味する. そのような成分の一つに着目し,第 \(k\) 成分であったとする.
このとき非基底変数の第 \(k\) 成分 \([\vec{x}_N]_k\) を基底解である \(0\) 値から正値にずらすと, 目的関数値はより改善すると考えられる. ここで次の二点が論点となる.
\([\vec{x}_N]_k\) をどれだけずらすか.つまり正値にずらす際の上限値 \(\theta\) は何か.
ずらすことでどの他の端点解が次に選ばれるか,つまりピボット操作すべき変数は何か.
それらは次のとおりである.
\(\vec{x}_B = B^{-1}\vec{b} - B^{-1}N\vec{x}_N\) より, \([\vec{x}_N]_{i^{\prime}} = \delta_{i^{\prime},k} [\vec{x}_N]_k\) を代入して整理すると次が得られる 1\(\delta_{i,k}\) は Kronecker の \(\delta\) である.つまり \(\delta_{i,k}\) は \(i=k\) のときに限り \(1\) で,他は \(0\) の値をとる..
ここで \(\vec{N}_k\) は非基底行列 \(N\) の第 \(k\) 列目でできるベクトルである.
また便宜のために,\(\vec{\beta} = B^{-1}\vec{b}\) および \(\vec{\nu} = B^{-1}\vec{N}_k\) を定めた.
さて \([\vec{x}_N]_k\) は \(\vec{x}_B\geq \vec{0}\) を満たして正値にずらさなければならない. すると (8) より,正値にずらす際の上限値 \(\theta\) が得られる(Dantzig ルール).
ここで \(\vec{\beta}\) と \(\vec{\nu}\) の第 \(i\) 成分をそれぞれ \(\beta_i\) および \(\nu_i\) と書いた.
注釈
\(\nu_i>0\) なる \(i\) が一つもないとき,\([\vec{x}_N]_k\) は問題の制約条件に違反することなく,幾らでも大きくして,目的関数値を改善することができる. これはつまり問題が非有界であることを意味する.
以上によって求められた \(\theta\) まで,\([\vec{x}_N]_k\) を増やしたとすると, \(\vec{x}_B = \vec{\beta} - \theta\vec{\nu}\) となる. 特に,\(J_k = \operatorname*{argmin}_i(\beta_i/\nu_i)\) の元 \(j\) についての成分は \(0\) となる.
つまり \(J_k\) のある一つの元 \(j\) で定まる基底変数 \([\vec{x}_B]_j\) と,非基底変数 \([\vec{x}_N]_k\) とをピボット操作の対象とすればよい.
以上の手続きを (有界である場合に) 最適解が得られるまで繰り返す手法が単体法である.
注釈
手続きの中で逆行列 \(B^{-1}\) が要求されている箇所があるが,必ずしも直接に求める必要はない. 逆行列は計算コストが高く,できることならこれを避けたいものである. 今の場合は,例えば \(\vec{\pi} = (B^{\top})^{-1}\vec{c}_B\) については, \(B^{\top}\vec{\pi} = \vec{c}_B\) というように一次方程式に戻して評価すればよい.
逆行列の話題以外にも,この種の数値計算のテクニックをいろいろと使うわけであるが,ここでは割愛している.
注釈
\(J_k\) は集合であり,一般には複数の要素がある.もし,その場合には,\(0\) となる基底変数が複数存在することになる.すると,ピボット操作で選ばなかった基底変数についても,退化したものは \(0\) となっているものがあることになる.こうなると,\(\theta\) の定義式から,ピボット操作後の反復で \(\theta=0\) となってしまい,単に \(0\) 同士を交換することになり,目的関数値は改善しない.退化している基底変数同士で交換し続けていると,再び同じ実行可能基底解に戻ってくることもあり,これを 循環 とか 巡回 (cycling)といい,無限ループに陥ってしまう.
収束性に関しては,循環を起こさないようにする対策を施すことにより,単体法は有限回の反復で実行結果を得られるということが知られている.有名な対策として Bland [1] の最小添字規則を用いた基底変数選択などがある.
3.4. まとめ#
まとめると,(退化が生じない)単体法の手続きは次のとおりである.
初期解として実行可能基底解 \((\vec{x}_B,\vec{x}_N) = (\vec{\beta},\vec{0})\) を選ぶ.ここで \(\vec{\beta} = B^{-1}\vec{b}\) と置いた.
単体乗数 \(\vec{\pi} = (B^{\top})^{-1}\vec{c}_B\) を計算する.
最適性条件 \(\vec{\gamma} \geq \vec{0}\) を評価する.満たされているならば,最適解が得られたため,手続きを終える.そうでないならば,条件を破っているある一つの成分 \(k\) を選び,これに対応する非基底変数 \([\vec{x}_N]_k\) に着目する.
\(\vec{\nu} = B^{-1}\vec{N}_k\) を計算する.\(\vec{\nu}\) のすべての成分が \(0\) 以下ならば,非有界であるため,手続きを終了する.そうでなければ,次の手続きへ.
\(J_k = \operatorname*{argmin}_i(\beta_i/\nu_i)\) の元 \(j\) を一つ選ぶ.
\([\vec{x}_N]_k \to \theta = \min_{i\in\{1,\ldots,m\}} (\beta_i / \nu_i)\) と更新する.
基底変数を \(\vec{x}_B \to \vec{\beta} - \theta\vec{\nu}\) と更新する.このとき,特に \([\vec{x}_B]_j = 0\) である.
\([\vec{x}_N]_k\) と \([\vec{x}_B]_j\) についてピボット操作する.手続き 2 へ.
上記の手続きが終了するとき,最適解が得られるか,または非有界と判定されるかの何れかの結果となる.
3.5. 例題#
PySIMPLE のチュートリアルにもある 油田計画問題 について,単体法を適用して,最適解を求めてみよう. この問題は線形最適化問題として次のように定式化できる. 但し,\(s_1,s_2,s_3,s_4\) はスラック変数である.
そして,次の等式標準形として整理できる.
ここで,次のとおりに記号を定めた.
こうして整理した問題に対して,単体法を適用しよう.
まず,係数行列 \(A\) のサイズから,\((m,n)=(4,6)\) とわかるので,基底変数と非基底変数の総数はそれぞれ \(4,(6-4=)2\) である. よって,基底変数ベクトル \(\vec{x}_B\) と非基底変数ベクトル \(\vec{x}_N\) を次のように設定して,単体法を開始する.
以下,縦書きするベクトルについて,成分をカンマで区切って,例えば \(\vec{x}_B = [x,y,s_1,s_2]\) などと横書きで表記する. また,反復2以降は略記する.
- 反復1
(開始設定から)実行可能基底解 \((\vec{x}_B,\vec{x}_N)=(\vec{\beta},\vec{0})\) として,次を選ぶ.
(16)#\[P_1 = \vec{\beta} = [5,5,23,26]\]単体乗数 \(\vec{\pi}\) を \([0,0,180,160]\) と求めて,現在の実行可能基底解についての目的関数値が求められる.
(17)#\[f(\vec{x}) = \vec{\pi}^{\top}\vec{b} = 1700\]相対費用係数ベクトル \(\vec{\gamma}\) を求めて,最適性条件を評価する.
(18)#\[\vec{\gamma} = [-180,-160]\]すべての成分が非負ではないので,先に求めた実行可能基底解は最適基底解ではない. 最適性条件を破っている非基底変数は複数あるが,ここでは \([\vec{x}_N]_1\) に着目する.
\(\vec{\nu}\) を求めて,有界性を評価する.
(19)#\[\vec{\nu} = [1,0,6,4]\]すべての成分が \(0\) 以下ではないので,非有界ではない.
\(\vec{\nu}\) の正成分について,\(J_k=\operatorname*{argmin}_{i\in \{1,2,3,4\}}(\beta_i/\nu_i)\) を求めて,有界性を評価する.
(20)#\[J_1 = \{3\}\]候補が複数ないので,退化していないともわかる.
非基底変数 \([\vec{x}_N]_1\) の値を次で更新する.
(21)#\[[\vec{x}_N]_1 = s_3 \to \theta = \frac{23}{6}\]基底変数ベクトルを \(\vec{x}_B = \vec{\beta} - \theta\vec{\nu}\) と更新する.
(22)#\[\vec{x}_B \to [7/6,5,0,32/3]\]\([\vec{x}_N]_1=s_3\) と \([\vec{x}_B]_3 = s_1\) についてピボット操作する.
- 反復2
\(P_2 = \vec{\beta} = [7/6, 5, 23/6, 32/3]\)
\(\vec{\pi} = [30,0,0,130]\) より,\(f(\vec{x}) = 1010\) である.
\(\vec{\gamma} = [30,-130]\) より,\([\vec{x}_N]_2\) に着目する.
\(\vec{\nu} = [-1/6,1,1/6,16/3]\) より,有界である.
\(J_2 = \{4\}\)
\([\vec{x}_N]_2 = s_4 \to \theta = 2\)
\(\vec{x}_B \to [3/2, 3, 7/2, s_2\to 0]\)
\([\vec{x}_N]_2=s_4\) と \([\vec{x}_B]_4=s_2\) についてピボット操作する.
- 反復3
\(P_3 = \vec{\beta} = [3/2, 3, 7/2, 2]\)
\(\vec{\pi} = [55/4, 195/8, 0, 0]\) より,\(f(\vec{x}) = 750\) である.
\(\vec{\gamma} = [55/4,195/8]\) より,最適性条件が満たされている.よって,先に求めた実行可能基底解は最適基底解である.故に,最適値は \(750\) であり,すべての手続きを終える.
以上より,単体法の反復は三回で終えることができた.
図 3.8 に示すように,実行可能領域の端点を順に巡って,最適解に到達していることがわかる.
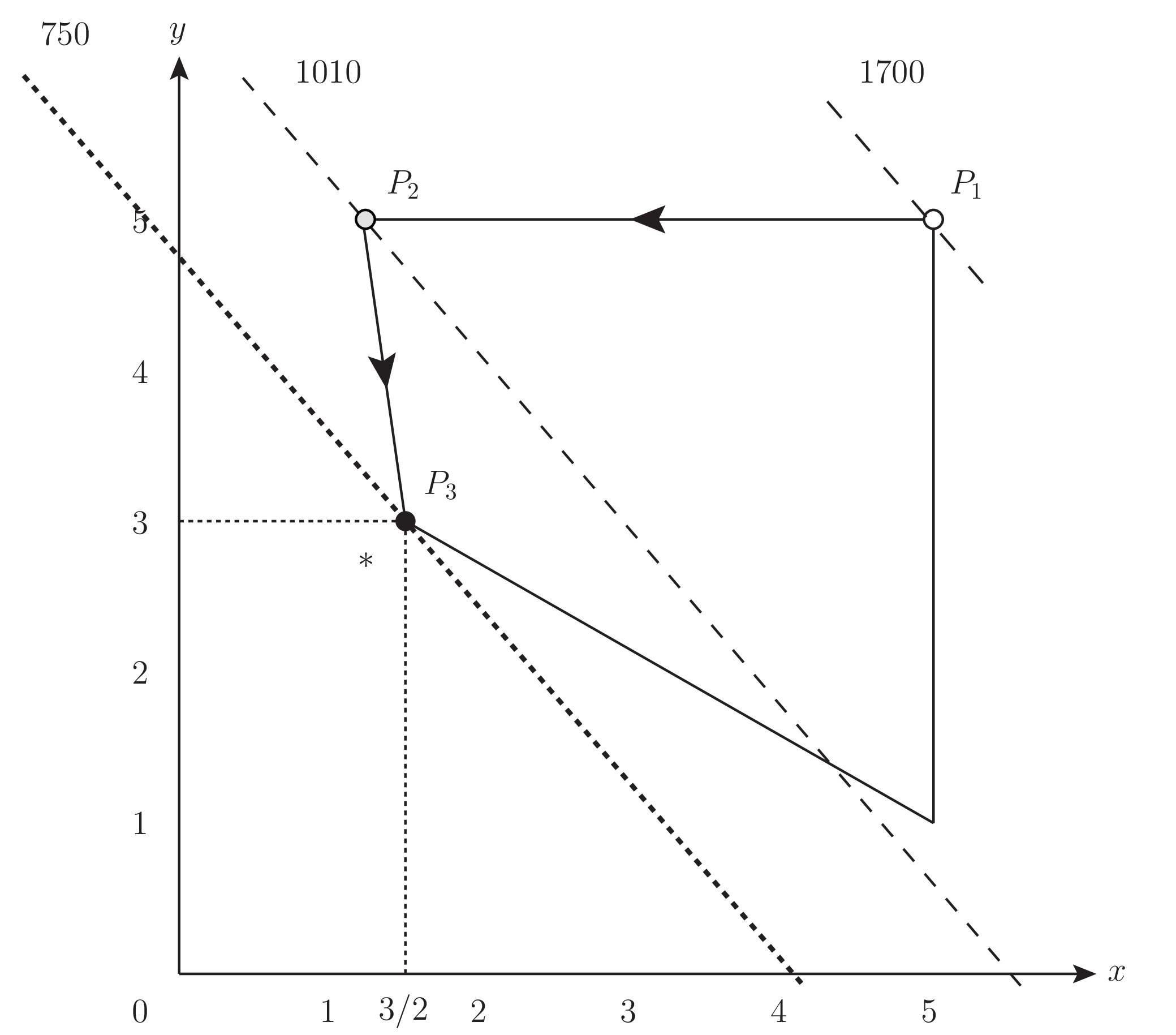
図 3.8 油田計画問題への単体法の適用#
図の破線状の直線とその数値は目的関数の等高線とその値を表し,実行可能領域の境界に矢印を引いて,解が隣接している端点 \(P_1,P_2,P_3\) を遷移していく様子を描いている. 単体法によって,実行可能基底解 \((\vec{\beta},\vec{0})\) で \(\vec{\beta}\) は次のように遷移した.
これらは幾何学的には四次元空間のある一点をそれぞれ示している. しかし,我々にとって興味があるのは,そのうち,第一成分と第二成分について射影した二次元平面 \((x,y)\) である.
つまり,\([5,5]\to[7/6,5]\to[3/2,3]\) と遷移していることになり, その図示は四次元空間を二次元平面に射影したものとなっている.
関連
用語集
参考文献
Robert G Bland. New Finite Pivoting Rules for the Simplex Method. Mathematics of Operations Research, 2(2):103–107, mar 1977. URL: http://www.jstor.org/stable/3689647.
バシェク・フバータル. 線形計画法(上). 啓学出版, 1986. URL: https://dl.ndl.go.jp/pid/12607925.
バシェク・フバータル. 線形計画法(下). 啓学出版, 1988. URL: https://dl.ndl.go.jp/pid/12607923.
Vašek Chvátal. Linear Programming. W.H.Freeman & Co Ltd, 1983. ISBN 9780716715870.
久保幹夫, 田村明久, and 松井知己. 応用数理計画ハンドブック. 朝倉書店, 2002. ISBN 978-4-254-27021-1. URL: https://www.asakura.co.jp/detail.php?book_code=27021.
福島雅夫. 新版 数理計画入門. 朝倉書店, 2011. ISBN 978-4-254-28004-3. URL: https://www.asakura.co.jp/detail.php?book_code=28004.
引用書式
