1. 数理最適化の共通項目#
1.1. 導入#
数理最適化を述べる上で,共通する項目を以下にまとめる. 基本的な用語および概念ばかりであるが,理論的な側面を述べるためには欠かせない事柄ばかりである.
1.2. 枠組#
数理最適化問題,変数,制約条件,目的関数
数理最適化問題 (mathematical optimization) とは「与えられた条件の下で, 望ましさの尺度を表す何らかの関数 \(f\) の最小値(最大値)を求め, さらにその最小値(最大値)を与える不特定要素の値を決定する」という問題である. このときの条件を制約条件 (constraint),関数 \(f\) を目的関数 (objective function),そして不特定要素としている問題の記述に含まれる決定すべき量を変数 (variable) という. 数理最適化問題はまた数理計画問題 (mathematical programming) ともいう.
注釈
数理最適化問題は様々な局面で現れる訳だがおよそ次の傾向がある.
制約条件の陽な形を問うとき,これは問題に応じて様々な経済的または社会的な意味を持つが,共通してある有限な資源を意味することが多い.
目的関数の陽な形を問うとき,多くは共通して金銭や能率といった人が実生活でとかく気にする量を意味することが多い.
数学的な定式化による数理最適化問題の分類は,必ずしも現実の問題の分類に従わない.
数理最適化問題は基本的に原因と結果を目的関数の構成に求める. つまり目的関数が扱う対象とは,問題にしている系の指標であり,系の変化の現れ (結果) と捉える. そして系の変化は実行可能領域に於ける目的関数の変数変化であり,それら以外に依存する変数はないと仮定する.
Tip
数理最適化の用語は応用分野が多岐にわたることもあってか,異称が特に多く,応用する分野に特有な用語が優先されることがある. 変数は決定変数 (desicion variable),制約条件は拘束条件,束縛条件 (restriction condition),目的関数は効率関数 (efficiency function) など,基本的な用語ですら幾つかの異称がある.
Tip
Mathematical programming は computer programming とは別に使われてきたが,近年は後者の意味が強まり,混乱を招くようになった. こうした背景から,米国の数理計画学会 (Mathematical Programming Society (MPS)) は 2010 年 6 月 4 日の会員投票(賛成 457,反対 127,棄権 38)を経て,数理最適化学会 (Mathematical Optimization Society (MOS)) へと改称された [1].
実行可能領域,実行可能解
変数の定義域は制約条件を満たす値の範囲によって定まるが,これを数理最適化問題の文脈では特に実行可能領域 (feasible region) という. そして実行可能領域に属する各点を実行可能解 (feasible solution) または許容解という.
最適値,最適解
実行可能解のうち,目的関数の最適値 (最小値または最大値) を与える解を最適解 (optimal solution) という. 通常,最適解とは実行可能領域全体で最も良い解のことを意味し,このことを特に強調する場合は大域的最適解 (global optimal solution) という. これに対して,実行可能領域の一部で,最適値を与える解のことを局所的最適解 (local optimal solution) という.単に局所解ということもある.
注意
大域的最適解は唯一とは限らない.また局所的最適解が大域的最適解の場合もある.
上記の定義から,制約条件の下,目的関数の最適値を与える解を最適解といい,単に制約条件のみを満たす場合は実行可能解ともいうことができる.
1.3. 有界性,線形性#
有界,非有界
大小比較が可能な数の範囲を扱うとき, 上 (下) に有界 (bounded) とは,その数の範囲がある値 \(M\) (\(m\)) 以下 (以上)であることをいう. 単に有界というときは上にも下にも有界であることを意味することが多い. そして有界でないことを非有界 (unbounded) という.
例えば非負実数からなる集合 \(\mathbb{R}_{\geq0}\) を数の範囲として扱うとき, \(\mathbb{R}_{\geq0}\) の任意の元 \(x\) は \(0\) 以上であるから,下に有界である. 一方でどんな実数 \(X\) についても任意の元 \(x\in\mathbb{R}_{\geq0}\) に対して \(x\leq X\) を満たすことはできないから,上には有界ではない (上に非有界).
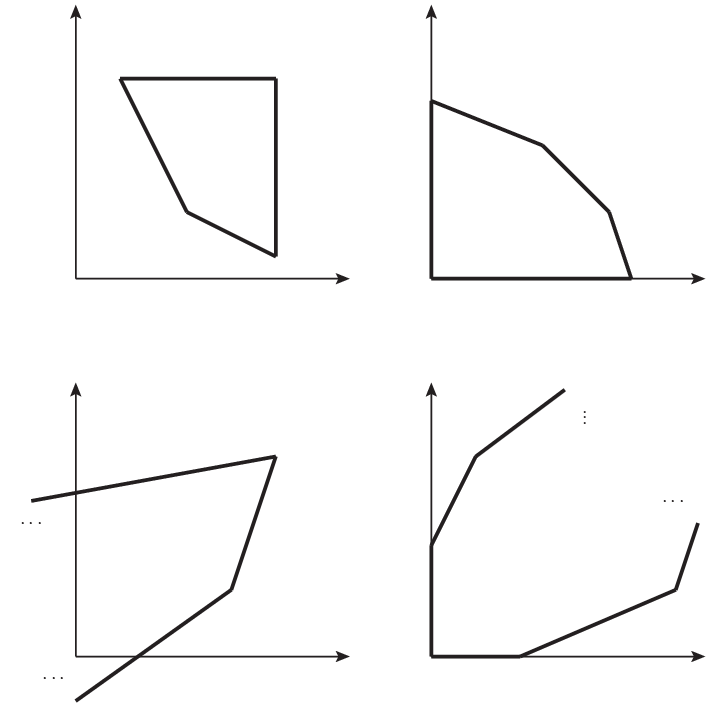
図 1.1 有界な領域(上二つ)と非有界な領域(下二つ)#
注釈
数理最適化の文脈では目的関数値が幾らでも大きく (小さく) できてしまわないかの議論をする場合に, そのような自明な議論から距離を置くために,有界,非有界の用語がよく用いられる.
スラック変数
スラック変数 (slack variable) または余裕変数とは不等式を等式に置き換えるための中間変数をいう. 不等号の情報はスラック変数それ自身の定義域として置換される.
例えば \(2x+3\leq 7\) という不等式は,\(2x+3+s = 7\) という等式について \(s\geq 0\) の下で \(x\) を求めることと同値である. このとき導入した \(s\) がスラック変数である.
線形性,非線形性
変数 \(x,y\) および定数 \(\alpha\) について,次を満たす写像 \(f\) が考えられるとき,この写像は線形 (linear) であるという.
また線形でないことを非線形 (nonlinear) という.
注意
変数 \(x\) についての一次式 \(\alpha x + \beta\) は線形関数ではなく,アフィン関数 (affine function) であり,非線形関数である. しかしながら,定数項 \(\beta(\neq 0)\) を区別することに力を割くことはほとんどなく,用語を徹底することは無用に記述が複雑になることにも繋がってしまう. 実際,目的関数の定数項は最適化に影響せず,そして,制約式は一方の辺にすべて定数項を移せるため,もう一方の辺は線形関数とできる. このため,厳密にはアフィン関数も許容されるところでも,単に線形と称することがよくある.
1.4. 凸性#
凸性
集合 \(C\) の任意の元 \(x,y\) および任意の \(\alpha\in [0,1]\) に対して,次が満たされるとき,集合 \(C\) を凸集合 (convex set) という.
このとき上記の線形結合を特に凸結合 (convex combination) という. また凸集合でない集合を非凸集合 (nonconvex set) という.
より一般に複数の元 \(\{x_i\}_{i\in I}\) についての凸結合は次で与えられる.
ここで各 \(i\) について,\(\alpha_i\geq0\) かつ \(\sum_{i\in I}\alpha_i = 1\) である.
凸集合の定義から明らかなように, 凸集合とは任意の二点間を結ぶ線分上のどの点も元の集合に含まれるような集合のことである.
Tip
数学ジョーク
凸集合の凸は凸ではないという有名なジョークがある. これは由々しきことだと思ったある若者は,複数の凸を上手くくっつけて,何とかして凸集合にしようと試みたという. そして,費やしてしまった時間を振り返って,彼は古代人の象形文字を呪った.
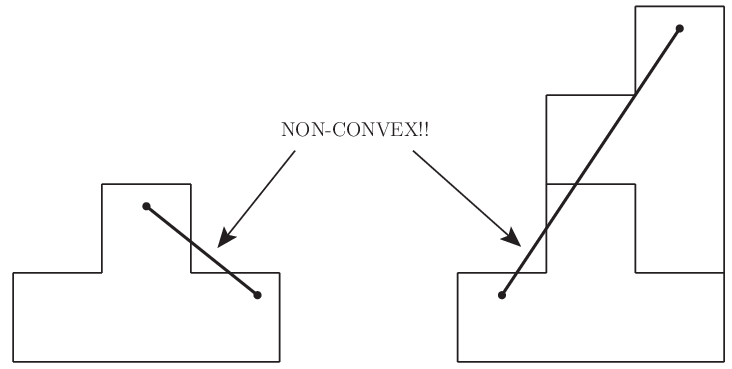
図 1.3 このジョークのおかげで,凸性の幾何学的意味を忘れることはないだろう.#
端点
凸集合 \(C\) に属する点 \(x\in\mathbb{R}^n\) が,それとは異なる \(C\) の二点 \(u,v(\neq v)\) の次の凸結合として表すせ ない とき,\(x\) を \(C\) の端点 (extreme point) という.
隣接する端点
二つの端点 \(x_1,x_2\) を結ぶ線分 \(L\) 上のいかなる点も,これら二つの端点の凸結合としてしか表せないとき,これら端点は互いに隣接しているという.
辺
集合 \(S\) に属する互いに異なる点 \(u,v\) を結ぶ線分 \(L\) を考える. \(L\) の端点 \(u,v\) を除いた内部の任意の点が,\(S\setminus L\) の二点の凸結合で表すせ ない とき,この線分 \(L\) を \(S\) の辺という.
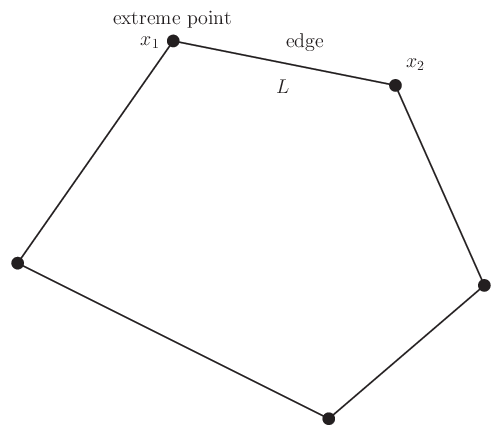
図 1.5 隣接する端点と辺#
関連
参考文献
Name Change: Mathematical Optimization Society. 2010. URL: https://www.mathopt.org/?nav=mps_namechange.
矢部博. 工学基礎 最適化とその応用. 数理工学社, 第2版 edition, 2024. ISBN 978-4-86481-111-8. URL: https://www.saiensu.co.jp/search/?isbn=978-4-86481-111-8&y=2024.
淀繁弘. 科学新興社 モノグラフ 27 線形計画法. 科学新興社, 1971.
福島雅夫. 新版 数理計画入門. 朝倉書店, 2011. ISBN 978-4-254-28004-3. URL: https://www.asakura.co.jp/detail.php?book_code=28004.
引用書式
