2.7 最大流問題
この節では,有向グラフをもとにしたデータ構造であるネットワークに関する基本的な問題の一つである最大流問題を取り上げます.最大流問題とは,ネットワーク上で始点(Source)から終点(Sink)まで流すことができる量の最大値を求める問題です.ただし,各辺には流すことができる量の上限が与えられています.さらに,始点と終点以外の点については,「流入してくる総量と流出していく総量は一致する」という関係(「保存則」と言います)が成り立つ必要があります.最大流問題は,配送や通信の分野などで応用が可能です.
例題
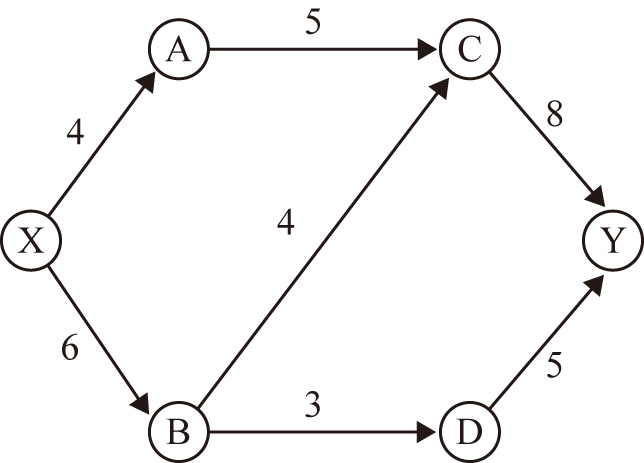
ある企業は,X町にある製粉工場で製造した小麦粉をY市のレストランに納めています.この際,下の図のように,製粉工場からレストランまで輸送する間にいくつかの問屋を経由しています.また,2つの地点の間で1日に運べる小麦粉の量の上限(kg)が図の数字の通りに決まっています.この時,製粉工場からレストランへ1日に納めることのできる小麦粉は最大で何kgでしょうか.ただし,各問屋は他の地点から輸送されてきた小麦粉を全て他の地点に輸送するものとします.
まず変数として,ネットワーク上で始点(X町の製粉工場)から終点(Y市のレストラン)へ1日に輸送する小麦粉の量(今後は「総輸送量」と呼びます)と各辺に対し輸送する小麦粉の量を用意します.こうすると,目的関数は変数「総輸送量」自身となります.
次に,制約条件について考えます.まず,2点間の輸送量については,負の値は許さず,対応する辺に与えられている上限を超えてはならないという制約条件が必要です.このことは,上下限制約として表現できます.さらに,各地点に対しては保存則が成立している必要があります.ただし,製粉工場については,各地点への輸送量の和が総輸送量と一致するということになります.また,レストランについては,各地点からの輸送量の和が総輸送量と一致しなければなりません.
以上のことから,この例題は次のように定式化できます.
| 変数 | |
| 総輸送量 | |
| 製粉工場からA地点への輸送量 | |
| 製粉工場からB地点への輸送量 | |
| A地点からC地点への輸送量 | |
| B地点からC地点への輸送量 | |
| B地点からD地点への輸送量 | |
| C地点からレストランへの輸送量 | |
| D地点からレストランへの輸送量 | |
| 目的関数(最大化) | |
| 総輸送量 | |
| 制約条件 | |
| 製粉工場での輸送量 | |
| A地点での輸送量保存則 | |
| B地点での輸送量保存則 | |
| C地点での輸送量保存則 | |
| D地点での輸送量保存則 | |
| レストランでの輸送量 | |
| 製粉工場からA地点への輸送量の上下限 | |
| 製粉工場からB地点への輸送量の上下限 | |
| A地点からC地点への輸送量の上下限 | |
| B地点からC地点への輸送量の上下限 | |
| B地点からD地点への輸送量の上下限 | |
| C地点からレストランへの輸送量の上下限 | |
| D地点からレストランへの輸送量の上下限 | |
これをC++SIMPLEで記述すると以下のようになります.
// 変数の宣言 Variable total(name = "製粉工場からレストランへの総輸送量"); Variable f_XA(name = "製粉工場から地点 A への輸送量"); Variable f_XB(name = "製粉工場から地点 B への輸送量"); Variable f_AC(name = "地点 A から地点 C への輸送量"); Variable f_BC(name = "地点 B から地点 C への輸送量"); Variable f_BD(name = "地点 B から地点 D への輸送量"); Variable f_CY(name = "地点 C からレストランへの輸送量"); Variable f_DY(name = "地点 D からレストランへの輸送量"); // 総輸送量の最大化 Objective obj(name = "製粉工場からレストランへの総輸送量(目的関数)", type = maximize); obj = total; // 各地点での輸送量 total == f_XA + f_XB; f_XA == f_AC; f_XB == f_BC + f_BD; f_AC + f_BC == f_CY; f_BD == f_DY; f_CY + f_DY == total; // 輸送量に関する上下限制約 0 <= f_XA <= 4; 0 <= f_XB <= 6; 0 <= f_AC <= 5; 0 <= f_BC <= 4; 0 <= f_BD <= 3; 0 <= f_CY <= 8; 0 <= f_DY <= 5; // 求解して値を出力する solve(); f_XA.val.print(); f_XB.val.print(); f_AC.val.print(); f_BC.val.print(); f_BD.val.print(); f_CY.val.print(); f_DY.val.print(); total.val.print();
このモデルファイルを実行させると,
製粉工場から地点 A への輸送量 = 4 製粉工場から地点 B への輸送量 = 6 地点 A から地点 C への輸送量 = 4 地点 B から地点 C への輸送量 = 3.28106 地点 B から地点 D への輸送量 = 2.71894 地点 C からレストランへの輸送量 = 7.28106 地点 D からレストランへの輸送量 = 2.71894 製粉工場からレストランへの総輸送量 = 10
という表示がされ,1日に最大10kg小麦粉を納めることができるという結果を確認できます.
ここで,C++SIMPLEでの記述について,より簡潔な形に書き直していくことにします.そのために,都市の集合という概念を導入します.また,2点間の輸送量の上限値を定数として外部から与えることにします.すると,定式化については次のように書き直すことができます.
| 集合 | |
| 都市の集合 | |
| 変数 | |
| 総輸送量 | |
| iからjへの輸送量 | |
| 目的関数(最大化) | |
| 総輸送量 | |
| 定数 | |
| iからjへの輸送量の上限 | |
| 制約条件 | |
| 製粉工場での輸送量 | |
| 問屋での輸送量の保存則 | |
| レストランでの輸送量 | |
| iからjへの輸送量の上下限 | |
これより,C++SIMPLEでの記述は次のようなものになります.
// 集合と添字 Set City; Element i(set = City), j(set = City), k(set = City); // パラメータ Parameter upper(name = "輸送量の上限", index = (i, j)); // 変数 Variable total(name = "製粉工場からレストランへの総輸送量"); Variable f(index = (i, j)); // 目的関数 Objective obj(name = "製粉工場からレストランへの総輸送量(目的関数)", type = maximize); obj = total; // 各地点での輸送量 total == sum(f["X", j], j); sum(f[k, j], j) == sum(f[j, k], j), k != "X", k != "Y"; sum(f[i, "Y"], i) == total; // 輸送量に関する上下限制約 0 <= f[i, j] <= upper[i, j]; // 求解 solve(); // 結果出力 total.val.print();
なお,実行時には次のcsvファイルを与えます.
輸送量の上限, A, B, C, D, X, Y A, 0, 0, 5, 0, 0, 0 B, 0, 0, 4, 3, 0, 0 C, 0, 0, 0, 0, 0, 8 D, 0, 0, 0, 0, 0, 5 X, 4, 6, 0, 0, 0, 0 Y, 0, 0, 0, 0, 0, 0
上に戻る