2.10 pメディアン問題
施設をどの地点に配置すると最適なのかを求める施設配置問題は,都市計画などに応用されています.施設配置問題の中から,この節でpメディアン問題を,次の節でpセンター問題を取り上げます.なお,本チュートリアルでは各地点は需要を有する地点(今後は「需要点」と呼びます)でありさらに施設を配置することが可能な地点でもあると仮定します.
まず,メディアンについて説明します.メディアンとは各需要点から施設を配置した地点(今後は「施設点」と呼びます)への移動距離の総和を最小にする点のことです.そして,このメディアンを求める問題のことをメディアン問題と呼びます.なお,一般にはどの程度の需要があるかは需要点ごとに異なりますので重み付きの総移動距離を最小にすることになります.また,施設を1箇所ではなくp箇所に配置するような場合にpメディアン問題と呼びます.
例題
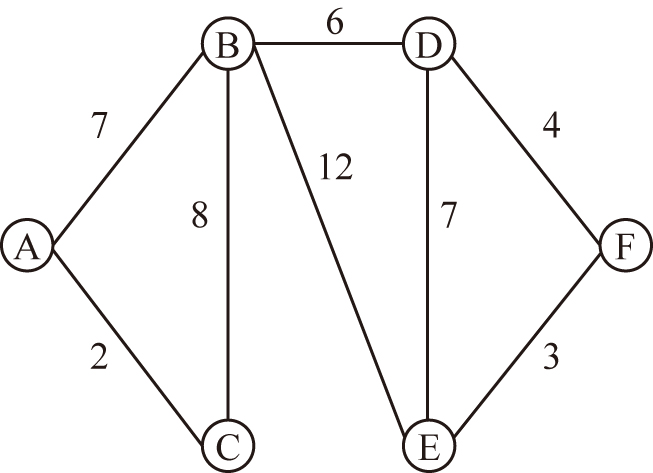
ある企業は,A市からF市までの6市の中から2つの市に新たにデパートを出店しようと考えています.この時,出店地までの総移動距離を最小にするためにはどの市に出店すると良いでしょうか.なお,各市の人口は左下の表のようになっています.また,2市間の距離は右下の図のようになっています.ただし,直接結ばれていない2都市間の距離は他の都市を経由したときの最短距離を採用します.
| 都市 | 人口 |
|---|---|
| A市 | 800 |
| B市 | 550 |
| C市 | 780 |
| D市 | 600 |
| E市 | 1020 |
| F市 | 360 |
まず,この問題では各都市に対しデパートを出店するのかどうかを表す変数が必要であることがわかります.しかし,これだけでは各都市からどちらの出店地が近いのかを求める必要があり,複雑な式になってしまいます.そこで,都市iを都市jのデパートに配分する場合1,そうでない場合は0を取るような0-1変数を導入します.なお,
の時には都市iにデパートを出店し,
の時には出店しないという解釈をします.
次に,制約条件について考えていきます.先ほど述べたように,は都市iに出店するかどうかを表しています.この例題では2都市に出店しますので,
は2である必要があります.また,各都市について近い方のデパートに配分しなければなりません(同距離の場合には任意にどちらかを選択することになります).
を用いて表現すると,各iについて
が1であるということになります.最後に,今のままですと出店していない都市に配分されてしまう可能性があります.これを防ぐためには,
の場合に
となってはいけないという制約条件が必要です.言い換えると,
は
より大きい値をとらないということになります.よって,式で表すと
となります.ただし,この制約条件は
の場合には無意味ですから
の場合のみで十分であることに注意してください.
目的関数は,重み付きの総移動距離ということになります.まず,都市iから都市jへの移動距離はの場合にのみ考慮する必要があります.よって,まず2市i, j間の距離と
の積を求めます.そして,jについて和をとることで都市iからの重みなしの移動距離が得られます.そして,この移動距離に重みである人口を掛けあわせることで都市iからの重みをつけた移動距離を得ます.重みをつけた移動距離を全ての都市について求め,和をとることで目的関数である重み付きの総移動距離となります.なお,図より2都市間の距離は次の表の通りになることが分かります.
| A市 | B市 | C市 | D市 | E市 | F市 | |
|---|---|---|---|---|---|---|
| A市 | 0 | 7 | 2 | 13 | 19 | 17 |
| B市 | 7 | 0 | 8 | 6 | 12 | 10 |
| C市 | 2 | 8 | 0 | 14 | 20 | 18 |
| D市 | 13 | 6 | 14 | 0 | 7 | 4 |
| E市 | 19 | 12 | 20 | 7 | 0 | 3 |
| F市 | 17 | 10 | 18 | 4 | 3 | 0 |
以上のことをまとめると,次のように定式化できます.
| 0-1変数 | |
| 0または1をとる出店するのかと最も近い出店地はどこなのかを表す変数 | |
| 目的関数(最小化) | |
| 重み付き総移動距離 | |
| 制約条件 | |
| 2都市に出店 | |
| A市は1箇所に配分 | |
| B市は1箇所に配分 | |
| C市は1箇所に配分 | |
| D市は1箇所に配分 | |
| E市は1箇所に配分 | |
| F市は1箇所に配分 | |
| 出店している都市に配分 | |
この結果をそのままC++SIMPLEで記述すると次のようになります.
// 変数の宣言
IntegerVariable
x_AA(type = binary), x_AB(type = binary), x_AC(type = binary),
x_AD(type = binary), x_AE(type = binary), x_AF(type = binary),
x_BA(type = binary), x_BB(type = binary), x_BC(type = binary),
x_BD(type = binary), x_BE(type = binary), x_BF(type = binary),
x_CA(type = binary), x_CB(type = binary), x_CC(type = binary),
x_CD(type = binary), x_CE(type = binary), x_CF(type = binary),
x_DA(type = binary), x_DB(type = binary), x_DC(type = binary),
x_DD(type = binary), x_DE(type = binary), x_DF(type = binary),
x_EA(type = binary), x_EB(type = binary), x_EC(type = binary),
x_ED(type = binary), x_EE(type = binary), x_EF(type = binary),
x_FA(type = binary), x_FB(type = binary), x_FC(type = binary),
x_FD(type = binary), x_FE(type = binary), x_FF(type = binary);
// 重み付き総移動距離の最小化
Objective total_distance(type = minimize);
total_distance = 800 * (7 * x_AB + 2 * x_AC + 13 * x_AD + 19 * x_AE + 17 * x_AF) +
550 * (7 * x_BA + 8 * x_BC + 6 * x_BD + 12 * x_BE + 10 * x_BF) +
780 * (2 * x_CA + 8 * x_CB + 14 * x_CD + 20 * x_CE + 18 * x_CF) +
600 * (13 * x_DA + 6 * x_DB + 14 * x_DC + 7 * x_DE + 4 * x_DF) +
1020 * (19 * x_EA + 12 * x_EB + 20 * x_EC + 7 * x_ED + 3 * x_EF) +
360 * (17 * x_FA + 10 * x_FB + 18 * x_FC + 4 * x_FD + 3 * x_FE);
// 2 都市に出店する
x_AA + x_BB + x_CC + x_DD + x_EE + x_FF == 2;
// 各都市を配分する
x_AA + x_AB + x_AC + x_AD + x_AE + x_AF == 1;
x_BA + x_BB + x_BC + x_BD + x_BE + x_BF == 1;
x_CA + x_CB + x_CC + x_CD + x_CE + x_CF == 1;
x_DA + x_DB + x_DC + x_DD + x_DE + x_DF == 1;
x_EA + x_EB + x_EC + x_ED + x_EE + x_EF == 1;
x_FA + x_FB + x_FC + x_FD + x_FE + x_FF == 1;
// 出店しない都市には配分しない
x_AB <= x_BB; x_AC <= x_CC; x_AD <= x_DD; x_AE <= x_EE; x_AF <= x_FF;
x_BA <= x_AA; x_BC <= x_CC; x_BD <= x_DD; x_BE <= x_EE; x_BF <= x_FF;
x_CA <= x_AA; x_CB <= x_BB; x_CD <= x_DD; x_CE <= x_EE; x_CF <= x_FF;
x_DA <= x_AA; x_DB <= x_BB; x_DC <= x_CC; x_DE <= x_EE; x_DF <= x_FF;
x_EA <= x_AA; x_EB <= x_BB; x_EC <= x_CC; x_ED <= x_DD; x_EF <= x_FF;
x_FA <= x_AA; x_FB <= x_BB; x_FC <= x_CC; x_FD <= x_DD; x_FE <= x_EE;ところで,この記述ですと都市の数が増えた場合に記述が大変であるなどの理由で汎用的ではありません.そこで,モデルファイルを汎用的なものにしていくことにします.そのためには,生データをできるだけ外部から与える必要があります.ここでは,人口と距離に関するデータをデータファイルから与えることにします.この時,様々なデータに対応できるように都市の集合という概念を導入しておきます.すると,定式化について次のように書き直せます.
| 集合 | |
| 都市の集合 | |
| 0-1変数 | |
| 0または1をとる出店するのかとどこに配分されるのかを表す変数 | |
| 定数 | |
| 都市iから都市jまでの距離 | |
| 都市iの人口 | |
| 目的関数(最小化) | |
| 重み付き総移動距離 | |
| 制約条件 | |
| 2都市に出店 | |
| 各都市は1箇所に配分 | |
| 出店している都市に配分 | |
上記の式をC++SIMPLEで記述すると,次のようになります.なお,Nuorium Optimizerでの実行時には都市の集合の具体的な要素はデータファイルから自動的に認識します.また,simple_printf()を用い出店する都市のみを表示するように工夫しました.
// 集合と添字
Set City;
Element i(set = City), j(set = City);
// パラメータ
Parameter distance(name = "2 都市間の距離", index = (i, j));
Parameter population(name = "都市の人口", index = i);
// 変数
IntegerVariable x(index = (i, j), type = binary);
// 目的関数
Objective total_distance(name = "総移動距離", type = minimize);
total_distance = sum(population[i] * sum(distance[i, j] * x[i, j], (j, i != j)), i);
// 制約条件
sum(x[i, i], i) == 2;
sum(x[i, j], j) == 1;
x[i, j] <= x[j, j], i != j;
// 求解
solve();
// 結果出力
simple_printf("%s 市に出店する.\n", i, x[i, i].val == 1);なお,実行時に次の2都市間の距離を表すcsvファイル(左)と都市の人口を表すdatファイル(右)を与えます.
2 都市間の距離, A, B, C, D, E, F A, 0, 7, 2, 13, 19, 17 B, 7, 0, 8, 6, 12, 10 C, 2, 8, 0, 14, 20, 18 D, 13, 6, 14, 0, 7, 4 E, 19, 12, 20, 7, 0, 3 F, 17, 10, 18, 4, 3, 0
都市の人口 = [A] 800 [B] 550 [C] 780 [D] 600 [E] 1020 [F] 360 ;
このモデルを実行すると次の表示がされ,A市とE市に出店すると良いことがわかります.
A 市に出店する. E 市に出店する.
上に戻る