数理最適化セミナーのご案内

2.8 最小費用流問題

　前節の最大流問題では，小麦粉の輸送を例にネットワークに流れる量をできるだけ多くしようという方針で最適化を行いました．このため，小麦粉を輸送する際にかかる燃料費などの様々なコストを考慮していませんでした．また，製粉工場から1日に出荷する小麦粉の量が決まっているような場合には別の方針で最適化を行う必要があります．

　決まった量をネットワーク上で始点から終点まで流す際にかかる費用（コスト）を最小にしようという問題のことを最小費用流問題といいます．なお，最大流問題のときと同様に，保存則が成立する必要があります．また，「決まった量」が1である場合には最小路問題と呼ばれ，カーナビゲーションシステムでのルート探索や鉄道の経路案内などに応用されています．

例題

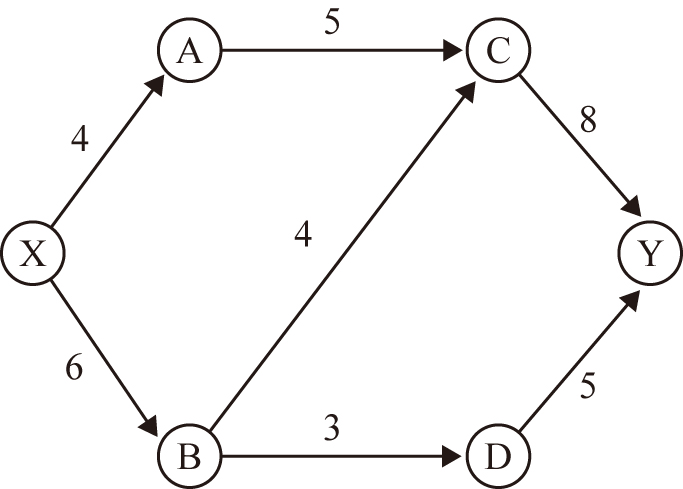
　ある企業は，X町の製粉工場で製造した小麦粉をY市のレストランまで1日に8kg納めています．この際，右下の図のように，製粉工場からレストランまで輸送する間にいくつかの問屋を経由しています．また，2つの地点の間で1日に運べる小麦粉の量の上限（kg）が図の数字のように決まっています．さらに，2つの地点の間で小麦粉を1kg輸送する毎に左下の表に書かれている費用がかかります．このとき，小麦粉を8kg製粉工場からレストランへ輸送する際にかかる総費用は最低いくらでしょうか．ただし，各問屋は他の地点から輸送されてきた小麦粉を全て他の地点に輸送するものとします．

輸送元 輸送先 1kgあたりの費用
製粉工場X A 250
製粉工場X B 200
A C 270
B C 300
B D 220
C レストランY 190
D レストランY 170

　

　定式化について，前節の最大流問題の時との違いは

  • 総輸送量（前節の例題でのtotalという変数）が8に決まっている．
  • 目的関数が総費用の最小化に変わっている．

の2点です．この2点以外については，前節の例題と同じ定式化となりますので必要に応じて前節を参考にしてください．なお，総費用は各輸送ルートについて「小麦粉1kgあたりの費用」と「輸送した小麦粉の量」の積を求め総和をとることで求められます．

　以上のことから，この例題は次のように定式化できます．

変数
$f_{XA}$ 製粉工場からA地点への輸送量
$f_{XB}$ 製粉工場からB地点への輸送量
$f_{AC}$ A地点からC地点への輸送量
$f_{BC}$ B地点からC地点への輸送量
$f_{BD}$ B地点からD地点への輸送量
$f_{CY}$ C地点からレストランへの輸送量
$f_{DY}$ D地点からレストランへの輸送量
　
目的関数（最小化）
$250f_{XA} + 200f_{XB} + 270f_{AC} + 300f_{BC} + 220f_{BD} + 190f_{CY} + 170f_{DY}$ 総費用
　
制約条件
$8 = f_{XA} + f_{XB}$ 製粉工場での輸送量
$f_{XA} = f_{AC}$ A地点での輸送量の保存則
$f_{XB} = f_{BC} + f_{BD}$ B地点での輸送量の保存則
$f_{AC} + f_{BC} = f_{CY}$ C地点での輸送量の保存則
$f_{BD} = f_{DY}$ D地点での輸送量の保存則
$f_{CY} + f_{DY} = 8$ レストランでの輸送量
$0 \le f_{XA} \le 4$ 製粉工場からA地点への輸送量の上下限
$0 \le f_{XB} \le 6$ 製粉工場からB地点への輸送量の上下限
$0 \le f_{AC} \le 5$ A地点からC地点への輸送量の上下限
$0 \le f_{BC} \le 4$ B地点からC地点への輸送量の上下限
$0 \le f_{BD} \le 3$ B地点からD地点への輸送量の上下限
$0 \le f_{CY} \le 8$ C地点からレストランへの輸送量の上下限
$0 \le f_{DY} \le 5$ D地点からレストランへの輸送量の上下限

　この結果をC++SIMPLEで記述すると以下のようになります．

// 変数の宣言
Variable f_XA(name = "製粉工場から地点 A への輸送量");
Variable f_XB(name = "製粉工場から地点 B への輸送量");
Variable f_AC(name = "地点 A から地点 C への輸送量");
Variable f_BC(name = "地点 B から地点 C への輸送量");
Variable f_BD(name = "地点 B から地点 D への輸送量");
Variable f_CY(name = "地点 C からレストランへの輸送量");
Variable f_DY(name = "地点 D からレストランへの輸送量");

// 総費用の最小化
Objective totalcost(name = "総費用", type = minimize);
totalcost = 250 * f_XA + 200 * f_XB + 270 * f_AC + 
            300 * f_BC + 220 * f_BD + 190 * f_CY + 170 * f_DY;

// 各地点での輸送量
8 == f_XA + f_XB;
f_XA == f_AC;
f_XB == f_BC + f_BD;
f_AC + f_BC == f_CY;
f_BD == f_DY;
f_CY + f_DY == 8;

// 輸送量に関する上下限制約
0 <= f_XA <= 4;
0 <= f_XB <= 6;
0 <= f_AC <= 5;
0 <= f_BC <= 4;
0 <= f_BD <= 3;
0 <= f_CY <= 8;
0 <= f_DY <= 5;

// 求解して値を出力する
solve();
f_XA.val.print();
f_XB.val.print();
f_AC.val.print();
f_BC.val.print();
f_BD.val.print();
f_CY.val.print();
f_DY.val.print();
totalcost.val.print();

　このモデルを実行させると，

製粉工場から地点 A への輸送量 = 2
製粉工場から地点 B への輸送量 = 6
地点 A から地点 C への輸送量 = 2
地点 B から地点 C への輸送量 = 3
地点 B から地点 D への輸送量 = 3
地点 C からレストランへの輸送量 = 5
地点 D からレストランへの輸送量 = 3
総費用 = 5260

という表示がされ，結果を確認できます．

　ところで，このままの記述では都市の数が多い問題に応用することが困難です．そこで，都市の集合という概念を導入し，必要なデータを定数として外部から与えるようにすることで大規模な問題に対しても応用しやすいようにします．まず，この方針で定式化をしなおすと次のようになります．なお，保存則については「他の地点への輸送量の和」と「他の地点からの輸送量の和」の差のデータを外部から与える形式を取りました．ちなみに，この値が正の地点が製粉工場，負の地点がレストラン，そして0の地点が問屋ということになります．

集合
$City = \{ A, B, C, D, X, Y \}$ 都市の集合
　
変数
$f_{ij}, i \in City, j \in City$ iからjへの輸送量
　
定数
$upper_{ij}, i \in City, j \in City$ iからjへの輸送量の上限
$cost_{ij}, i \in City, j \in City$ iからjへの輸送の際にかかる小麦粉1kgあたりの費用
$supply_i, i \in City$ iでの流出量と流入量の差
　
目的関数（最小化）
$\displaystyle \sum_{j \in City} \sum_{i \in City} cost_{ij} \cdot f_{ij}$ 総費用
　
制約条件
$\displaystyle \sum_{j \in City} f_{kj} - \sum_{i \in City} f_{ik} = supply_k, \forall k \in City$ 各地点での流出量と流入量の差
$0 \le f_{ij} \le upper_{ij}, \forall i, j \in City$ iからjへの輸送量の上下限

　この定式化をし直した結果をC++SIMPLEで記述すると次のようになります．

// 集合と添字
Set City;
Element i(set = City), j(set = City), k(set = City);

// パラメータ
Parameter upper(name = "輸送量の上限", index = (i, j));
Parameter cost(name = "輸送費用", index = (i, j));
Parameter supply(name = "supply", index = k);

// 変数
Variable f(name = "輸送量", index = (i, j));

// 目的関数
Objective total_cost(name = "総費用", type = minimize);
total_cost = sum(cost[i, j] * f[i, j], (i, j));

// 各地点での流出量と流入量の差
sum(f[k, j], j) - sum(f[i, k], i) == supply[k];

// 輸送量に関する上下限制約
0 <= f[i, j] <= upper[i, j];

// 求解
solve();

// 結果出力
total_cost.val.print();

　なお，実行時には次の2つのcsvファイルと1つのdatファイルを与えます．

輸送量の上限, A, B, C, D, X, Y
A, 0, 0, 5, 0, 0, 0
B, 0, 0, 4, 3, 0, 0
C, 0, 0, 0, 0, 0, 8
D, 0, 0, 0, 0, 0, 5
X, 4, 6, 0, 0, 0, 0
Y, 0, 0, 0, 0, 0, 0
輸送費用, A, B, C, D, X, Y
A, 0, 0, 270, 0, 0, 0
B, 0, 0, 300, 220, 0, 0
C, 0, 0, 0, 0, 0, 190
D, 0, 0, 0, 0, 0, 170
X, 250, 200, 0, 0, 0, 0
Y, 0, 0, 0, 0, 0, 0
supply =
[A] 0 
[B] 0 
[C] 0 
[D] 0 
[X] 8 
[Y] -8
;
2.7 最大流問題
2.9 多品種流問題

 

 

上に戻る