数理最適化セミナーのご案内

2.9 多品種流問題

　今まで述べてきた最大流問題や最小費用流問題では，ネットワーク上を1種類のものしか流れていませんでした．しかし，現実世界ではネットワーク上を複数のものが流れるというケースがよくあります．多品種流問題は，複数の品物をそれぞれ始点から終点まで輸送するという場合に利用される問題で，通信など多くの分野で応用されています．

例題

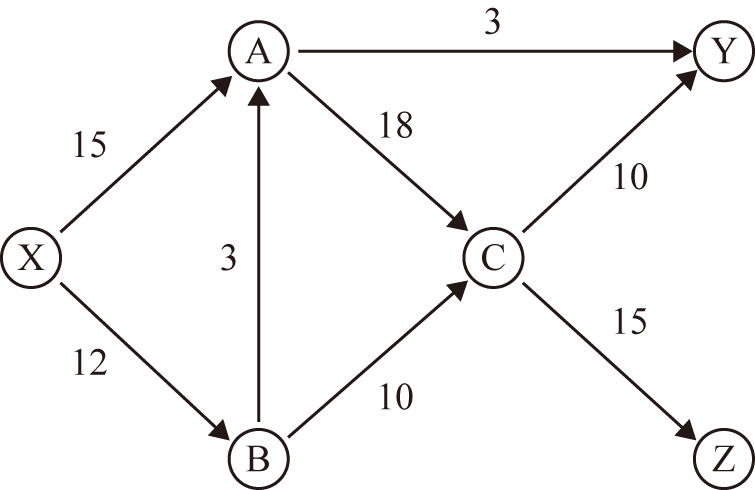
　ある企業は，X町の製粉工場で製造したパン用の小麦粉をY市のパン屋まで1日に8kg納めています．さらに，同じ製粉工場で製造したうどん用の小麦粉をZ市のうどん屋まで1日に13 kg納めています．この際，下の図のように，製粉工場からパン屋，製粉工場からうどん屋まで輸送する間にいくつかの問屋を経由しています．また，2つの地点の間で1日に運べるパン用の小麦粉とうどん用の小麦粉の合計量の上限（kg）が図の数字のように決まっています．さらに，2つの地点の間でパン用の小麦粉やうどん用の小麦粉を1kg輸送する毎に下の表に書かれているだけの費用がかかります．このとき，パン用の小麦粉とうどん用の小麦粉を決められた量だけ納める際にかかる総費用は1日につき最低いくらでしょうか．

輸送元 輸送先 パン用の小麦粉の輸送費 うどん用の小麦粉の輸送費
製粉工場X A 12 11
製粉工場X B 10 12
A C 4 5
A パン屋Y 11 -
B A 6 7
B C 11 9
C パン屋Y 9 -
C うどん屋Z - 5

　まず，各輸送ルートについてパン用の小麦粉の輸送量とうどん用の小麦粉の輸送量が変数として必要です．ただし，うどん屋にパン用の小麦粉を輸送したりパン屋にうどん用の小麦粉を輸送したりすることはありませんので，これらに対応する変数はここでは宣言しないことにします．

　次に，目的関数については最小費用流問題の時と同様に考えることになります．ただし，パン用の小麦粉とうどん用の小麦粉で輸送コストが異なる点には注意が必要です．

　最後に，制約条件を考えます．各輸送ルートについては問題文にあるようにパン用の小麦粉の輸送量とうどん用の小麦粉の輸送量の和が上限を超えないという制約条件が必要です．また，保存則については地点と商品に関し場合分けをする必要があります．さらに，「-1kg輸送する」ということはありえませんので変数について非負制約が必要です．

　以上のことから，次のように定式化できます．

変数
$PWheat_{XA}$, $UWheat_{XA}$ 製粉工場からA地点への輸送量
$PWheat_{XB}$, $UWheat_{XB}$ 製粉工場からB地点への輸送量
$PWheat_{AC}$, $UWheat_{AC}$ A地点からC地点への輸送量
$PWheat_{AY}$ A地点からパン屋への輸送量
$PWheat_{BA}$, $UWheat_{BA}$ B地点からA地点への輸送量
$PWheat_{BC}$, $UWheat_{BC}$ B地点からC地点への輸送量
$PWheat_{CY}$ C地点からパン屋への輸送量
$UWheat_{CZ}$ C地点からうどん屋への輸送量
　
目的関数（最小化）
$12PWheat_{XA} + 10PWheat_{XB} + 4PWheat_{AC} + 11PWheat_{AY} + 6PWheat_{BA} + 11PWheat_{BC} + 9PWheat_{CY} + 11UWheat_{XA} + 12UWheat_{XB} + 5UWheat_{AC} + 7UWheat_{BA} + 9UWheat_{BC} + 5UWheat_{CZ}$ 総輸送費
　
制約条件
$PWheat_{XA} + UWheat_{XA} \le 15$, $PWheat_{XB} + UWheat_{XB} \le 12$, $PWheat_{AC} + UWheat_{AC} \le 18$, $PWheat_{AY} \le 3$, $PWheat_{BA} + UWheat_{BA} \le 3$, $PWheat_{BC} + UWheat_{BC} \le 10$, $PWheat_{CY} \le 10$, $UWheat_{CZ} \le 15$ 各輸送ルートの輸送量の上限を超えない
$PWheat_{XA} + PWheat_{XB} = 8$, $PWheat_{AC} + PWheat_{AY} = PWheat_{XA} + PWheat_{BA}$, $PWheat_{BA} + PWheat_{BC} = PWheat_{XB}$, $PWheat_{CY} = PWheat_{AC} + PWheat_{BC}$, $8 = PWheat_{AY} + PWheat_{CY}$ パン用の小麦粉に関する保存則
$UWheat_{XA} + UWheat_{XB} = 13$, $UWheat_{AC} + UWheat_{AY} = UWheat_{XA} + UWheat_{BA}$, $UWheat_{BA} + UWheat_{BC} = UWheat_{XB}$, $UWheat_{CZ} = UWheat_{AC} + UWheat_{BC}$, $13 = UWheat_{CZ}$ うどん用の小麦粉に関する保存則
$PWheat_{XA} \ge 0$, $PWheat_{XB} \ge 0$, $PWheat_{AC} \ge 0$, $PWheat_{AY} \ge 0$, $PWheat_{BA} \ge 0$, $PWheat_{BC} \ge 0$, $PWheat_{CY} \ge 0$, $UWheat_{XA} \ge 0$, $UWheat_{XB} \ge 0$, $UWheat_{AC} \ge 0$, $UWheat_{BA} \ge 0$, $UWheat_{BC} \ge 0$, $UWheat_{CZ} \ge 0$ 輸送量に関する非負制約

　これをC++SIMPLEで記述すると次のようになります．

// 変数の宣言
Variable
  PWheat_XA, PWheat_XB, PWheat_AC, PWheat_AY, PWheat_BA, PWheat_BC, PWheat_CY,
  UWheat_XA, UWheat_XB, UWheat_AC, UWheat_BA, UWheat_BC, UWheat_CZ;

// 目的関数の宣言
Objective total_cost(name = "総輸送費", type = minimize);
total_cost = 12 * PWheat_XA + 10 * PWheat_XB + 4 * PWheat_AC + 11 * PWheat_AY +
             6 * PWheat_BA + 11 * PWheat_BC + 9 * PWheat_CY + 11 * UWheat_XA +
             12 * UWheat_XB + 5 * UWheat_AC + 7 * UWheat_BA + 9 * UWheat_BC +
             5 * UWheat_CZ;

// 輸送ルートごとの輸送量の上限
PWheat_XA + UWheat_XA <= 15;
PWheat_XB + UWheat_XB <= 12;
PWheat_AC + UWheat_AC <= 18;
PWheat_AY <= 3;
PWheat_BA + UWheat_BA <= 3;
PWheat_BC + UWheat_BC <= 10;
PWheat_CY <= 10;
UWheat_CZ <= 15;

// パン用の小麦粉に関する保存則
PWheat_XA + PWheat_XB == 8;
PWheat_AC + PWheat_AY == PWheat_XA + PWheat_BA;
PWheat_BA + PWheat_BC == PWheat_XB;
PWheat_CY == PWheat_AC + PWheat_BC;
8 == PWheat_AY + PWheat_CY;

// うどん用の小麦粉に関する保存則
UWheat_XA + UWheat_XB == 13;
UWheat_AC == UWheat_XA + UWheat_BA;
UWheat_BA + UWheat_BC == UWheat_XB;
UWheat_CZ == UWheat_AC + UWheat_BC;
13 == UWheat_CZ;

// 非負制約
PWheat_XA >= 0; PWheat_XB >= 0; PWheat_AC >= 0; PWheat_AY >= 0;
PWheat_BA >= 0; PWheat_BC >= 0; PWheat_CY >= 0;
UWheat_XA >= 0; UWheat_XB >= 0; UWheat_AC >= 0; UWheat_BA >= 0;
UWheat_BC >= 0; UWheat_CZ >= 0;

　ここで，C++SIMPLEでの記述をより簡潔なものにしていくことにします．そのためには，都市の集合の概念を導入し，さまざまなデータに対応できるようにすることが有効です．この際，輸送量の上限値などの具体的なデータを出来るだけ外部から与えるようにしておきます．

　すると，定式化については次のように表現できます．

集合
$City = \{ A, B, C, X, Y, Z \}$ 都市の集合
　
変数
$PWheat_{ij}, i \in City, j \in City$ iからjへのパン用の小麦粉の輸送量
$UWheat_{ij}, i \in City, j \in City$ iからjへのうどん用の小麦粉の輸送量
　
定数
$upper_{ij}, i \in City, j \in City$ iからjへの輸送量の上限
$PWheat\_cost_{ij}, i \in City, j \in City$ iからjへの輸送の際にかかるパン用の小麦粉1kgあたりの費用
$UWheat\_cost_{ij}, i \in City, j \in City$ iからjへの輸送の際にかかるうどん用の小麦粉1kgあたりの費用
$PWheat\_supply_i, i \in City$ iでのパン用の小麦粉の流出量と流入量の差
$UWheat\_supply_i, i \in City$ iでのうどん用の小麦粉の流出量と流入量の差
　
目的関数（最小化）
$\displaystyle \sum_{j \in City} \sum_{i \in City} (PWheat\_cost_{ij} \cdot PWheat_{ij} + UWheat\_cost_{ij} \cdot UWheat_{ij})$ 総輸送費
　
制約条件
$PWheat_{ij} + UWheat_{ij} \le upper_{ij}, \forall i,j \in City$ iからjへの輸送量の上限
$\displaystyle \sum_{j \in City} PWheat_{kj} - \sum_{i \in City} PWheat_{ik} = PWheat\_supply_k$, $\forall k \in City$ 各地点でのパン用の小麦粉に関する保存則
$\displaystyle \sum_{j \in City} UWheat_{kj} - \sum_{i \in City} UWheat_{ik} = UWheat\_supply_k$, $\forall k \in City$ 各地点でのうどん用の小麦粉に関する保存則
$0 \le PWheat_{ij}, \forall i, j \in City$ パン用の小麦粉の輸送量の非負制約
$0 \le UWheat_{ij}, \forall i, j \in City$ うどん用の小麦粉の輸送量の非負制約

　C++SIMPLEで記述すると次のようになり，先ほどのものより簡潔になっていることが分かります．

// 集合と添字
Set City;
Element i(set = City), j(set = City), k(set = City);

// パラメータ
Parameter upper(name = "輸送量の上限", index = (i, j));
Parameter PWheat_cost(name = "パン用の小麦粉の輸送費用", index = (i, j));
Parameter UWheat_cost(name = "うどん用の小麦粉の輸送費用", index = (i, j));
Parameter PWheat_supply(name = "PWheat_supply", index = k);
Parameter UWheat_supply(name = "UWheat_supply", index = k);

// 変数
Variable PWheat(name="パン用の小麦粉の輸送数", index=(i,j));
Variable UWheat(name="うどん用の小麦粉の輸送数", index=(i,j));

// 目的関数
Objective total_cost(name = "総輸送費", type = minimize);
total_cost = sum(PWheat_cost[i, j] * PWheat[i, j] + UWheat_cost[i, j] * UWheat[i, j], (i, j));

// 輸送ルートごとの輸送量の上限
PWheat[i, j] + UWheat[i, j] <= upper[i, j];

// パン用の小麦粉に関する保存則
sum(PWheat[k, j], j) - sum(PWheat[i, k], i) == PWheat_supply[k];

// うどん用の小麦粉に関する保存則
sum(UWheat[k, j], j) - sum(UWheat[i, k], i) == UWheat_supply[k];

// 非負制約
PWheat[i, j] >= 0;
UWheat[i, j] >= 0;

　なお，実行時には次の3つのcsvファイル（輸送量の上限・パン用の小麦粉の輸送費用・うどん用の小麦粉の輸送費用）と1つのdatファイル（PWheat_supplyおよびUWheat_supply）を与えます．

パン用の小麦粉の輸送費用, A, B, C, X, Y, Z
A, 0, 0, 4, 0, 11, 0
B, 6, 0, 11, 0, 0, 0
C, 0, 0, 0, 0, 9, 0
X, 12, 10, 0, 0, 0, 0
Y, 0, 0, 0, 0, 0, 0
Z, 0, 0, 0, 0, 0, 0
輸送量の上限, A, B, C, X, Y, Z
A, 0, 0, 18, 0, 3, 0
B, 3, 0, 10, 0, 0, 0
C, 0, 0, 0, 0, 10, 15
X, 15, 12, 0, 0, 0, 0
Y, 0, 0, 0, 0, 0, 0
Z, 0, 0, 0, 0, 0, 0
うどん用の小麦粉の輸送費用, A, B, C, X, Y, Z
A, 0, 0, 5, 0, 0, 0
B, 7, 0, 9, 0, 0, 0
C, 0, 0, 0, 0, 0, 5
X, 11, 12, 0, 0, 0, 0
Y, 0, 0, 0, 0, 0, 0
Z, 0, 0, 0, 0, 0, 0
PWheat_supply = [A]  0 [B]  0 [C]   0
                [X]  8 [Y] -8 [Z]   0;
UWheat_supply = [A]  0 [B]  0 [C]   0
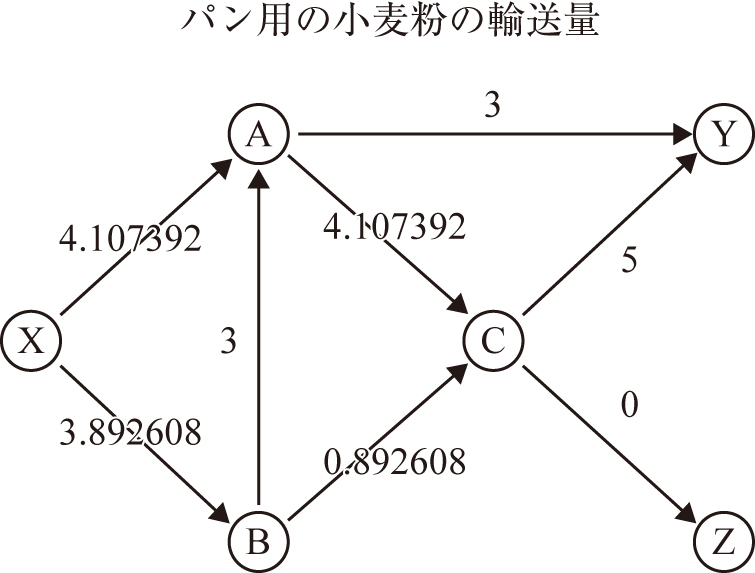
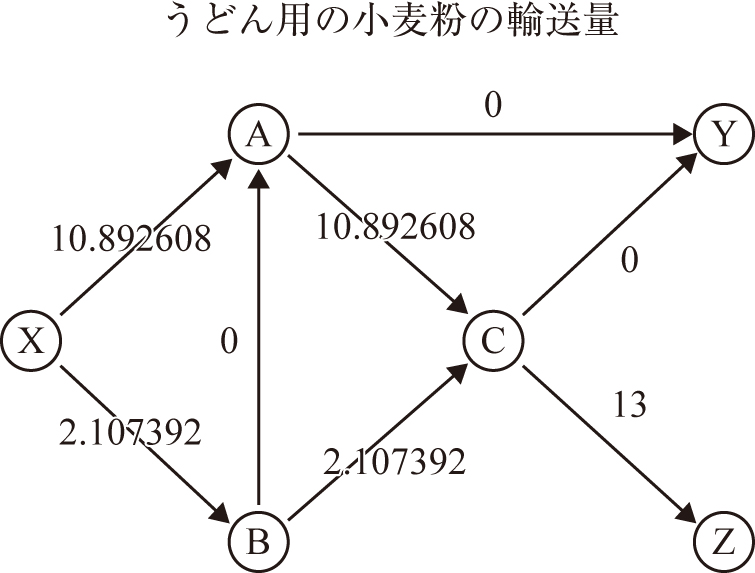
                [X] 13 [Y]  0 [Z] -13;

　このモデルを実行した結果から，総費用が494になるように輸送すると最適であり，例えば次の図のようにパン用の小麦粉とうどん用の小麦粉を輸送するとよいことが分かります．

2.8 最小費用流問題
2.10 pメディアン問題

 

 

上に戻る