数理最適化セミナーのご案内

2.13.2 基礎的なマス埋め割当問題

　ここではまず，マス目を埋めるだけの問題を考えていきます．

例題

　4×4のマス目があります．このマスに石を置きたいのですが，全ての縦横に関して石の数が2つになるように配置します．さてどのように置けば良いでしょうか．

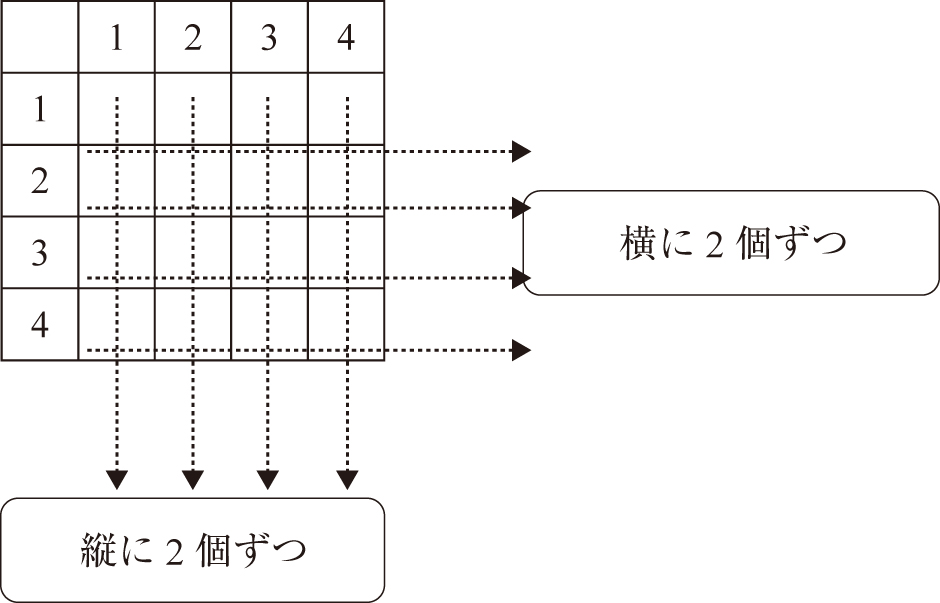
　この問題を定式化するためには，0-1変数を用いる必要があります．この問題の場合以下の図のように，各マスに対して0-1変数を対応させます．

  1 2 3 4
1 x11 x12 x13 x14
2 x21 x22 x23 x24
3 x31 x32 x33 x34
4 x41 x42 x43 x44

　

　定式化をすると以下のようになります．

0-1変数
$x_{11}$, $x_{12}$, $x_{13}$, $x_{14}$

$x_{21}$, $x_{22}$, $x_{23}$, $x_{24}$

$x_{31}$, $x_{32}$, $x_{33}$, $x_{34}$

$x_{41}$, $x_{42}$, $x_{43}$, $x_{44}$		 それぞれのマスに石を置くならば1置かないならば0．
　
目的関数
　 この問題には目的関数はない
　
制約条件
$x_{11} + x_{12} + x_{13} + x_{14} = 2$ 1行目を横に見たときに石を2つ置く
$x_{21} + x_{22} + x_{23} + x_{24} = 2$ 2行目を横に見たときに石を2つ置く
$x_{31} + x_{32} + x_{33} + x_{34} = 2$ 3行目を横に見たときに石を2つ置く
$x_{41} + x_{42} + x_{43} + x_{44} = 2$ 4行目を横に見たときに石を2つ置く
$x_{11} + x_{21} + x_{31} + x_{41} = 2$ 1列目を縦に見たときに石を2つ置く
$x_{12} + x_{22} + x_{32} + x_{42} = 2$ 2列目を縦に見たときに石を2つ置く
$x_{13} + x_{23} + x_{33} + x_{43} = 2$ 3列目を縦に見たときに石を2つ置く
$x_{14} + x_{24} + x_{34} + x_{44} = 2$ 4列目を縦に見たときに石を2つ置く

　定式化した結果をC++SIMPLEで記述すると以下のようになります．

IntegerVariable x_11(type = binary);
IntegerVariable x_21(type = binary);
IntegerVariable x_31(type = binary);
IntegerVariable x_41(type = binary);

IntegerVariable x_12(type = binary);
IntegerVariable x_22(type = binary);
IntegerVariable x_32(type = binary);
IntegerVariable x_42(type = binary);

IntegerVariable x_13(type = binary);
IntegerVariable x_23(type = binary);
IntegerVariable x_33(type = binary);
IntegerVariable x_43(type = binary);

IntegerVariable x_14(type = binary);
IntegerVariable x_24(type = binary);
IntegerVariable x_34(type = binary);
IntegerVariable x_44(type = binary);

x_11 + x_12 + x_13 + x_14 == 2;
x_21 + x_22 + x_23 + x_24 == 2;
x_31 + x_32 + x_33 + x_34 == 2;
x_41 + x_42 + x_43 + x_44 == 2;

x_11 + x_21 + x_31 + x_41 == 2;
x_12 + x_22 + x_32 + x_42 == 2;
x_13 + x_23 + x_33 + x_43 == 2;
x_14 + x_24 + x_34 + x_44 == 2;

// 以下は出力用のプログラム
solve();
simple_printf("%d %d %d %d\n", x_11, x_12, x_13, x_14);
simple_printf("%d %d %d %d\n", x_21, x_22, x_23, x_24);
simple_printf("%d %d %d %d\n", x_31, x_32, x_33, x_34);
simple_printf("%d %d %d %d\n", x_41, x_42, x_43, x_44);

　このモデルをNuorium Optimizerで実行すると，最後に

0 1 0 1
0 0 1 1
1 1 0 0
1 0 1 0

という表示がされ，この例題の答えを確認できます．どの縦横にも二箇所ずつ石が置いてある（1と表示されている）のが分かります．

　さて，次にこの問題をC++SIMPLEの添字機能を用いてモデル化してみます．定式化は以下のように変更します．

集合
$I = \{ 1, 2, 3, 4 \}$ 行
$J = \{ 1, 2, 3, 4 \}$ 列
　
0-1変数
$x_{ij}, i \in I, j \in J$ マス$(i, j)$に石を置くならば$x_{ij} = 1$，置かないならば$x_{ij} = 0$とする．
　
目的関数
　 この問題には目的関数はない
　
制約条件
$\displaystyle \sum_i x_{ij} = 2, \forall j \in J$ 各列$j$は横に見たときに石を2つ置く
$\displaystyle \sum_j x_{ij} = 2, \forall i \in I$ 各行$i$は縦に見たときに石を2つ置く

　添字を用いることにより，以下のように簡単にモデル記述することができます．

// 集合と添字
Set I = "1 2 3 4";
Element i(set = I);
Set J = "1 2 3 4";
Element j(set = J);

// 変数
IntegerVariable x(type = binary, index = (i, j));
sum(x[i, j], i) == 2;
sum(x[i, j], j) == 2;

// 求解
solve();

// 結果出力
simple_printf("%d %d %d %d\n", x[i, j], x[i, j + 1], x[i, j + 2], x[i, j + 3], j == 1);
2.13.1 割当問題とは
2.13.3 仕事割当問題

 

 

上に戻る