B.2.3 分枝限定法
Nuorium Optimizerは,整数変数を含む線形/二次計画問題に対して以下のアルゴリズムが指定された場合,分枝限定法と呼ばれるアルゴリズムを用います.
- 単体法 (options.method = "simplex")
- 有効制約法(options.method = "asqp")
分枝限定法とは一般に元の問題の制約を一部緩和した問題(緩和問題)を繰り返し解くことにより厳密解を求めるアルゴリズムです.特に整数計画問題に適用される場合,緩和問題は整数変数を連続変数に緩和した問題(連続緩和問題)を考えます.
ここでは0-1整数変数を含む線形計画問題(目的関数を最小化する)の例を説明します.0-1整数変数は連続緩和すると上限値が1,下限値が0となる連続変数になることにご注意ください.
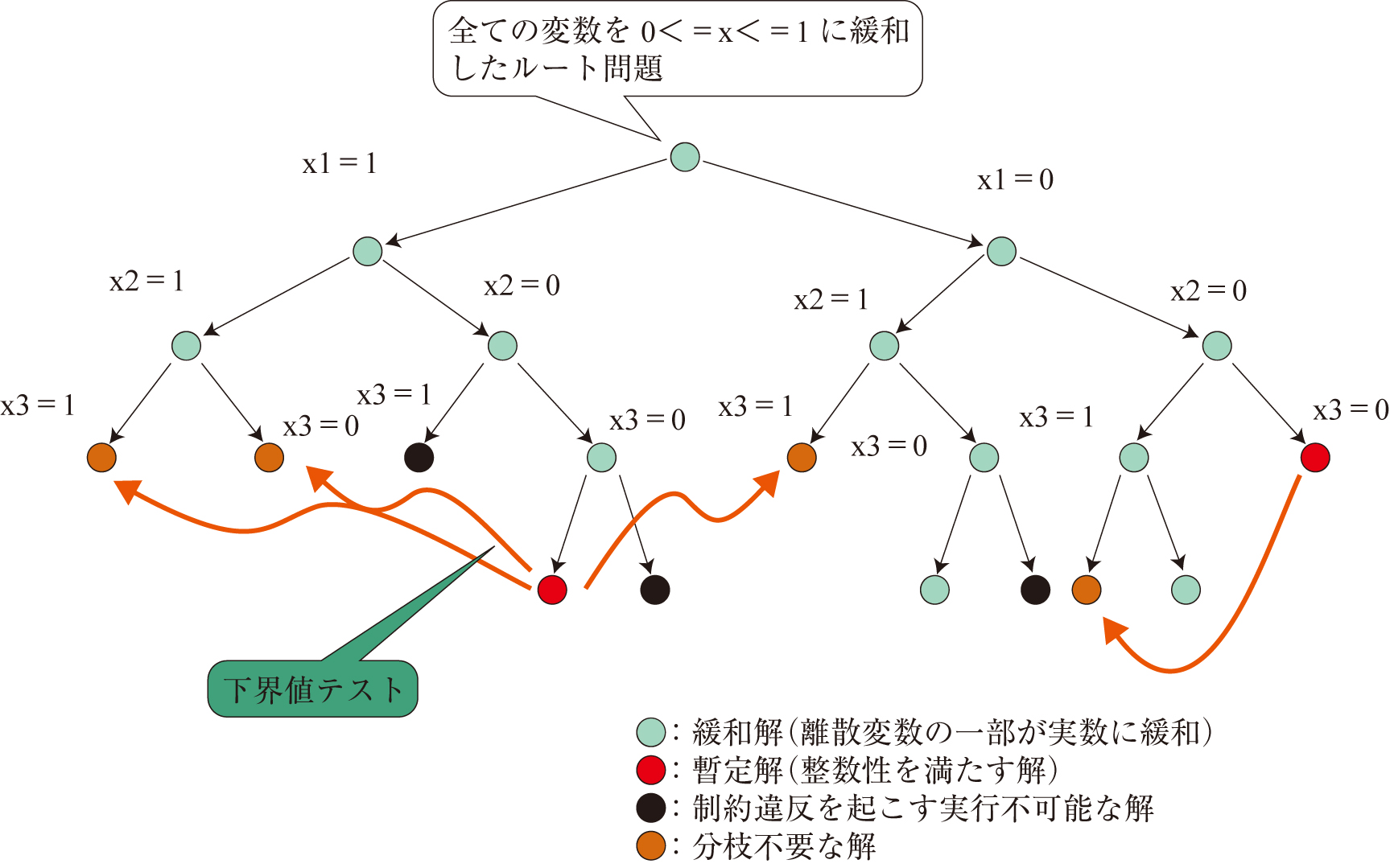
分枝限定法では緩和問題の解から整数になっていない変数を一つ選択し,0または1に固定する,という操作(分枝操作)を行います.この過程は次の図のような木(分枝木)の形に表すことができ,整数制約を満たす解はこの木の「葉」の部分(図の下側の先端部分)に現れます.
しかしながら,分枝操作だけでは「葉」が整数変数の数に対して指数的に増える可能性があり,現実的な規模の問題に対して効率の良い解法となりません.このため分枝限定法は,分枝木の 「分枝するごとに緩和問題の目的関数値が同じあるいは増大する」という性質を用いて枝の削減を行います(限定操作).具体的には,分枝時に緩和解がその時点で知られている暫定解(整数性を満たす解)よりも目的関数値が大きければ,それ以上分枝する必要がありません.例えば緩和解の目的関数値が11で,暫定解として10が得られていればそれ以上分枝して探索する必要がありません(上の図の橙色の解に相当).分枝限定法はこのような分枝操作と限定操作を繰り返し最適解を得るアルゴリズムです.
Nuorium Optimizerは更なる工夫により分枝限定法を高速化しています.
- ヒューリスティクス
- 通常の分枝限定法では緩和解が整数性を満たす時のみ暫定解が得られます.Nuorium Optimizer ではそれに加え,実行可能解探索を別のロジックで行うことにより効率よく暫定解を求めます.例えばヒューリスティクス RINS では,緩和解と暫定解を比較し,共通して整数となっている変数は固定し,解が非共通の変数を非固定にした状態で分枝限定法を新たに解くことで,実行可能解を得ようとします.
- 切除平面
- 整数計画問題では,整数性を考慮することにより「切除平面」と呼ばれる制約式を生成できます.この制約式を元の制約式に付与すると緩和解が改善するため,分枝木を小さくできます.ただし緩和問題のサイズは大きくなるため,トレードオフの調整が必要です.
- 前処理
- 整数計画問題は,最初の緩和問題を解く前に「前処理」により問題変換あるいは問題削減を行います.例えば「検針( probing )」と呼ばれる操作は0-1 変数を 0 あるいは 1 に固定しそこから実行不可能性が導かれるのであればどちらかに固定します.
これらの手法の具体的な求解オプションの設定方法については「整数計画法(simplex/asqp)に有効な求解オプション」の項に解説があります.
上に戻る